Геометричний зміст похідної

В курсі геометрії ви познайомились з означен­ням дотичної до кола: дотичною до кола нази­вається пряма, яка лежить в площині кола і має з колом лише одну спільну точку. Таке оз­начення дотичної не може бути перенесено на всі криві (парабола, синусоїда, гіпербола тощо).

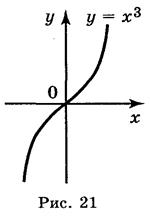
Наприклад, вісь ΟΥ має тільки одну спільну точку з графіком функції у = х³, проте її не мож­на вважати дотичною до кубічної параболи в точці 0 (рис. 21).

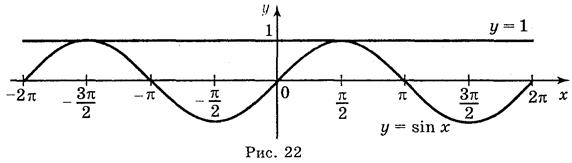
Пряма у = 1 і синусоїда у = sinx мають безліч спільних точок (рис. 22), проте пряму у = - 1 вважають дотичною до синусоїди.

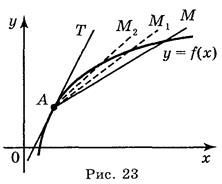Для введення означення дотич­ної до кривої розглянемо функцію у = f(x) і її графік — криву лінію (рис. 23). Нехай точки А і Μ нале­жать графіку функції у = f(x), про­ведемо січну AM.

Зафіксуємо точку А. Нехай точ­ка М, рухаючись по кривій, набли­жається до точки А. При цьому січна AM буде повертатися навко­ло точки А і в граничному поло­женні при наближенні точки М до точки А січна займе поло­ження прямої АТ. Пряму АТ називають дотичною до даної кри­вої в точці А.

Дотичною АТ до графіка функції у = f(x) в точці А називається граничне положення січної AM, коли точка М, рухаючись по кривій, наближається до точки А.

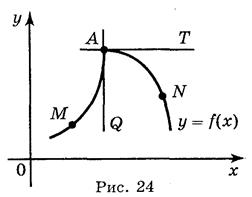Слід мати на увазі, що не в уся­кій точці кривої можна провести до неї дотичну. На рис. 24 зображено криву у = f(x), яка в точці А не має дотичної, бо якщо точка М буде на­ближатися до точки А по лівій час­тині кривої, то січна МА займе гра­ничне положення AQ.

Якщо точка N буде наближатися по правій частині кривої, то січна ΝΑ займе граничне положення AT. Одержуємо дві різні прямі AQ і АТ, це означає, що в точці А до даної кривої дотичної не існує.

Поставимо задачу: провести дотичну до графіка функції у = f(x) в точці А(х₀; у₀).

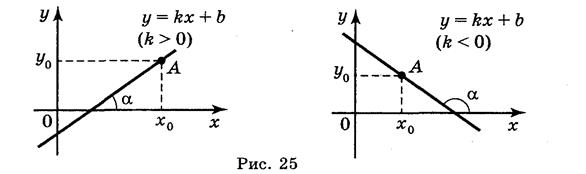
Дотична — це пряма, а положення прямої у= kx + b, яка проходить через точку А(х₀; у₀) визначається кутовим коефіцієнтом прямої k = tg α, де α — кут між прямою і додатнім напрямом осі ОХ (рис. 25).

Отже, провести дотичну до графіка означає знайти число k.

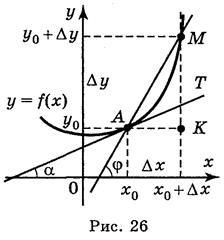
Нехай в точці А(х₀; у₀) (рис. 26) кривої у = f(x) існує дотична, визна­чимо кутовий коефіцієнт дотичної. Для цього:

1) Надамо аргументу х₀ приросту Δх, одержимо нове значення аргументу х₀ + Δх.

2) Знайдемо відповідний приріст функції: Δу = f(х₀ + Δх) - f(х₀)

3) Знайдемо відношення 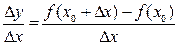. Із трикутника АМК маємо: 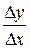= tg 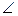МАК. Так як 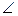ΜΑΚ = φ — куту нахилу січної AM з додатним напрямом осі ОХ, то 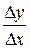= tg φ.