Вспомогательные расчеты для определения параметров а0 и а1 уравнения прямой и критерия статистической точности
Аналитического уравнения
| Годы | Товарные запасы, млн.грн. | t | t2 | yt | yt | |y - yt| | 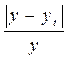 |
| 10,0 | - 4 | - 40,0 | 9,4 | 0,6 | 0,036 | ||
| 10,7 | - 3 | - 32,1 | 10,5 | 0,2 | 0,004 | ||
| 12,0 | - 2 | - 24,0 | 11,6 | 0,4 | 0,013 | ||
| 10,3 | - 1 | - 10,3 | 12,7 | 2,4 | 0,233 | ||
| 12,9 | 13,8 | 0,9 | 0,070 | ||||
| 16,3 | 16,3 | 14,9 | 1,4 | 0,086 | |||
| 15,6 | 31,2 | 16,0 | 0,4 | 0,026 | |||
| 17,8 | 53,4 | 17,1 | 0,7 | 0,039 | |||
| 18,0 | 72,0 | 18,2 | 0,2 | 0,011 | |||
| Итого | 123,6 | 66,5 | 124,2 | - | 0,520 |
Следовательно, 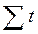 = 0. Тогда система нормальных уравнений примет вид:
= 0. Тогда система нормальных уравнений примет вид: 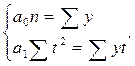 Отсюда,
Отсюда, 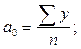
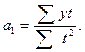
Следовательно, 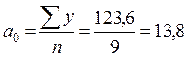 ;
; 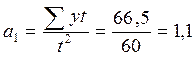 .
.
Таким образом, уравнение прямой, описывающей тенденцию из-менения товарных запасов за 1994-2002гг., примет вид: 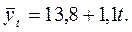
Подставив в это уравнение значение t получим выравненные (теоретические) показатели товарных запасов (табл. 8.3, гр.6). По приведенным расчетам можно сделать вывод о тенденции роста запасов, при этом в среднем ежегодно они возрастали на 1,1 млн.грн., о чем свидетельствует значение параметра а1 в уравнении прямой.
Определим критерий статистической точности анализируемого уравнения: 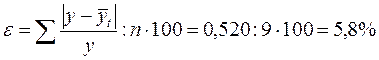 . Так как
. Так как 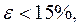 то можно заключить, что в данном случае аналитическое уравнение достаточно точно описывает эмпирические данные.
то можно заключить, что в данном случае аналитическое уравнение достаточно точно описывает эмпирические данные.
Пример 2.Имеются следующие данные о продаже трикотажных изделий в розничной торговой сети по кварталам за три года, млн.грн:
| Годы | Кварталы | |||
| I | II | III | IV | |
| Первый год | ||||
| Второй год | ||||
| Третий год |
Для анализа внутригодовой динамики продажи трикотажных изделий необходимо определить индексы сезонности.
Решение
По годовым показателям рассчитаем темпы роста:
Таблица 8.5
Динамика продажи трикотажных изделий в розничной
торговой сети региона
| Годы | Годовые уровни продажи три-котажных изделий, млн. грн | Темпы роста, % | |
| к предыдущему году | к первому году | ||
| Первый | - | 100,0 | |
| Второй | 103,2 | 103,2 | |
| Третий | 100,8 | 104,0 |
Представленный в нашем примере ряд динамики имеет цепные и базисные темпы роста, изменяющиеся незначительно. Для анализа внут-ригодовой динамики рядов, в которых наблюдается стабильность годо-вых уровней или имеет место незначительная тенденция роста (сниже-ние), изучать сезонность возможно с помощью метода простой средней:
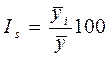 .
.
Применяя формулу средней арифметической простой, определим средние квартальные уровни за три года: 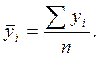
I квартал: 
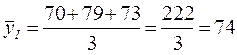 млн.грн.;
млн.грн.;
II квартал: 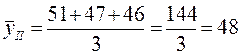 млн.грн и т.д. (табл. 8.6)
млн.грн и т.д. (табл. 8.6)
Исчислим общую среднюю (итог по гр.6 табл.8.6): 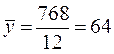 Определим за каждый квартал индексы сезонности:
Определим за каждый квартал индексы сезонности:
I квартал: 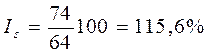 и т.д. (табл. 8.6).
и т.д. (табл. 8.6).
Таблица 8.6
Расчет индексов сезонности продажи трикотажных изделий в розничной сети региона по кварталам трех лет
| Годы и показатели | Кварталы | Итого за год | |||
| I | II | III | IV | ||
| 1 | 2 | 3 | 4 | 5 | 6 |
| Первый | |||||
| Второй | |||||
| Третий | |||||
| Итого: | |||||
| Средний уровень, млн.грн | |||||
| Индексы сезонности, % | 115,6 | 75,0 | 70,3 | 139,1 | 100,0 |
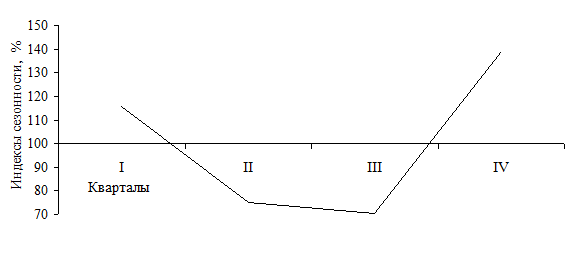
Рис. 8.2. График сезонности продажи трикотажных изделий по кварталам за три года.
По индексам сезонности можно наблюдать рост или снижение продажи трикотажных изделий в различное время года. Так, по проведенным расчетам очевидно, что наименьший спрос приходится на III квартал и наибольший – на IV квартал.
Сезонная волна, изображенная графически (рис 8.2), показывает, что ниже среднего уровня продажа трикотажных товаров наблюдается во II и III кварталах и выше среднего уровня она в I и IV кварталах года (осенний и зимний подъемы).
Пример 3. Имеются следующие данные о внутригодовой динамике поставок сельскохозяйственной продукции торговой фирме, тыс.т:
| Кварталы | Поставка, тыс. т | ||
| первый год | второй год | третий год | |
| I | 16,2 | 15,0 | 15,8 |
| II | 17,0 | 19,8 | 22,5 |
| III | 17,7 | 17,8 | 18,7 |
| IV | 15,1 | 16,8 | 17,2 |
Для анализа внутригодовой динамики поставки сельскохозяйственной продукции требуется исчислить индексы сезонности.
Решение
Для каждого года квартальные уровни укрупним до годовых и по ним исчислим темпы роста.
Таблица 8.7
Динамика поставки сельскохозяйственной
продукции торговой фирме
| Годы | Годовые уровни, тыс. т | Темпы роста, % | |
| к предыдущему году | к первому году | ||
| Первый | 66,0 | - | 100,0 |
| Второй | 69,4 | 105,2 | 105,2 |
| Третий | 74,2 | 106,9 | 112,4 |
Можно отметить, что ряд динамики имеет четкую тенденцию роста поставок, об этом свидетельствуют увеличивающиеся цепные и базисные темпы роста.
Для расчета индексов сезонности в таких рядах динамики применяют формулу: 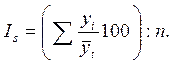
Определим теоретические значения 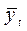 по уравнению:
по уравнению: 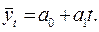
Для определения параметров а0 и а1 составим таблицу 8.8 со вспомогательными расчетами.
Таблица 8.8
Расчет параметров 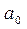 и
и 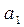 аналитического уравнения
аналитического уравнения
| Периоды | Поставка, тыс.т, 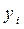 | t | t2 | yit | 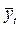 | 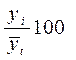 |
| Первый год | ||||||
| I кв. | 16,2 | -11 | -178,2 | 16,2 | 100,0 | |
| II кв. | 17,0 | -9 | -153,0 | 16,4 | 103,7 | |
| III кв. | 17,7 | -7 | -123,9 | 16,7 | 106,0 | |
| IV кв. | 15,1 | -5 | -75,5 | 16,9 | 89,3 | |
| Второй год | ||||||
| I кв. | 15,2 | -3 | -45,6 | 17,1 | 88,9 | |
| II кв. | 19,4 | -1 | -19,4 | 17,4 | 111,5 | |
| III кв. | 18,0 | 18,8 | 17,6 | 102,3 | ||
| IV кв. | 16,8 | 50,4 | 17,9 | 93,9 | ||
| Третий год | ||||||
| I кв. | 15,8 | 79,0 | 18,1 | 87,3 | ||
| II кв. | 22,5 | 157,5 | 18,3 | 117,5 | ||
| III кв. | 18,7 | 168,3 | 18,6 | 100,5 | ||
| IV кв. | 17,2 | 189,2 | 18,8 | 91,5 | ||
| Итого | 209,6 | 66,8 | 210,0 | - |
Определим параметры: 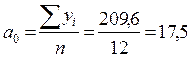 ;
; 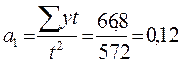
Следовательно, уравнение прямой примет вид: 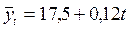 . Подставив в полученное уравнение значения t (квартальные), получим выравненные уровни ряда (табл. 8.8 гр. 6). Далее необходимо оп-ределить для каждого квартала процентные отношения эмпирических уровней ряда (yi) к теоретическим (
. Подставив в полученное уравнение значения t (квартальные), получим выравненные уровни ряда (табл. 8.8 гр. 6). Далее необходимо оп-ределить для каждого квартала процентные отношения эмпирических уровней ряда (yi) к теоретическим ( 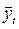 ), т.е.
), т.е. 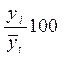 (табл.8.8 гр.7).
(табл.8.8 гр.7).
Таблица 8.9
Динамика поставок сельскохозяйственной продукции торговой фирме и расчет индексов сезонности
| Квар- талы | Фактические данные, yi | Выравненные данные, 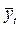 | Фактические данные в % к выравненным, 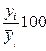 | Сумма про-центных отноше ний, (гр.8+ +гр.9+ +гр.10) | Индексы сезон- ности, 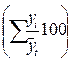 : : n : : n | ||||||
| первый год | второй год | третий год | первый год | второй год | третий год | первый год | второй год | третий год | |||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| I | 16,2 | 15,2 | 15,8 | 16,5 | 17,1 | 18,1 | 100,0 | 88,9 | 87,3 | 276,2 | 92,1 |
| II | 17,0 | 19,4 | 22,5 | 16,4 | 17,4 | 18,3 | 103,7 | 111,5 | 117,5 | 332,7 | 110,9 |
| III | 17,7 | 18,0 | 18,7 | 16,7 | 17,6 | 18,6 | 106,0 | 102,3 | 100,5 | 308,8 | 102,9 |
| IV | 15,1 | 16,8 | 17,2 | 16,9 | 17,9 | 18,8 | 89,3 | 93,9 | 91,5 | 274,7 | 91,6 |
| Итого | 66,0 | 69,4 | 74,2 | 66,2 | 70,0 | 73,8 | - | - | - | - |
Просуммируем полученные процентные отношения 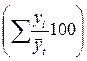 за три года по одноименным кварталам:
за три года по одноименным кварталам:
I кв. : 100,00 + 88,9 + 87,3 = 276,2;
II кв. : 100,3 + 111,5 + 117,5 = 332,3 и т. д. (табл. 8.9 гр.11).
Затем исчислим индексы сезонности (табл. 8.9 гр.12). Они характеризуют размеры поставок сельскохозяйственной продукции в зависимости от времени года. Наибольший удельный вес поставок приходится на второй и третий кварталы года.
Пример 4. На условных данных о грузообороте предприятий в одном из регионов необходимо произвести выравнивание по ряду Фурье. В таблице содержатся произведения у · соst, у · sint, необходи-мые для определения параметров уравнения по первой гармонике.
На основе полученных итоговых данных таблицы 8.10 находим:
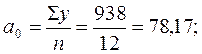
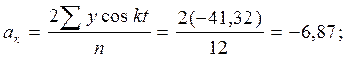
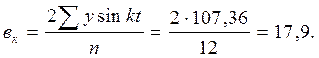
Отсюда: 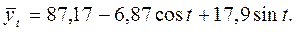
Подставляя в это уравнение значения соst, sint (из таблицы приложения 2) получим теоретические значения грузооборота 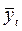 (см. гр. 5 табл. 8.10).
(см. гр. 5 табл. 8.10).
Таблица 8.10
Грузооборот транспортных предприятий региона и расчет параметров системы уравнения по ряду Фурье
| Месяц, t | Грузооборот, млрд. ткм, у | у соst | у sint | 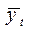 |
| 1 | 2 | 3 | 4 | 5 |
| 60,00 | 71,20 | |||
| 69,28 | 40,00 | 81,02 | ||
| 43,00 | 74,45 | 90,22 | ||
| 108,00 | 96,03 | |||
| - 67,00 | 116,04 | 97,10 | ||
| - 50,22 | 29,00 | 93,06 | ||
| - 70,00 | 85,04 | |||
| - 58,88 | - 34,00 | 76,50 | ||
| -45,00 | - 77,94 | 66,10 | ||
| - 70,00 | 60,26 | |||
| 29,00 | - 50,22 | 59,22 | ||
| 48,50 | - 28,00 | 63,26 | ||
| Итого | - 41,32 | 107,36 | 939,04 |
Параметры гармоники второго и высшего порядка рассчитываются аналогично, и их значения последовательно присоединяются к значениям первой гармоники. Опустив расчеты, запишем уравнение для выравнивания изучаемого ряда с учетом второй гармоники:
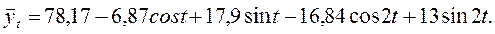
Подставив в данное уравнение конкретные значения соst,sint, sin2t, соs2t, получим выравненные данные грузооборота по месяцам. Расчет и сравнение остаточных дисперсий 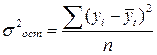 позволяет судить о том, какая гармоника наиболее близка к фактическим уровням ряда.
позволяет судить о том, какая гармоника наиболее близка к фактическим уровням ряда.
