Каноническая катастрофа сборки

Проведем анализу структуры критических точек функции .Для заданной пары критические точки функции определяются из условия

Дроби в коэффициентах подбирались как раз так, чтобы получилось уравнение простейшего вида.

Это уравнение кубическое по 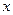, и поэтому оно имеет самое большее три и самое меньшее один вещественный корень.

Природа корней зависит от значени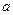й и 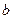, a именно от дискриминанта рассматриваемого кубического уравнения.

Если , имеются три различных вещественных корня, а если , то один вещественный и пара взаимно сопряженных комплексных корней. Если , то имеются три вещественных корня, но некоторые из них совпадают между собой: если , но или , то совпадают два корня, а если и , то совпадают все три корня.

Геометрически это означает, что природа корней, а значит и равновесие машины, зависит от положения свободного конца резинки по отношению к кривой, определяемой в координатах уравнением .

На рисунке 1.27 она изображена жирной линией.

Рисунок 1.27 - Кривая, описываемая уравнениеем

Подразделим плоскость (обозначим ее через С) на пять подмножеств:

- заштрихованную область 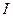«внутри» кривой;

- область «вне» ее;

- две ветви и кривой и начало Р.

Точки , лежащие в 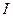, характеризуются условием , а точки, лежащие в , условием .

Поэтому:

если лежит в , то имеется один вещественный корень;

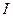если лежит в , то имеются три различных вещественных корня;

если лежит в или в , то имеются три вещественных корня, но два из них совпадают между собой. Для совпадение происходит с наименьшим корнем, а для – с наибольшим;

если совпадает с , т. е. , то имеются три совпадающих вещественных корня (все они равны 0).

Эти возможности проиллюстрированы на рис. 7.4 а. Вид соответствующих потенциальных функций (7.1) показан на рис. 7.4, б.

Мы видим, что имеет один минимум, если , два минимума и между ними максимум, если , один минимум и одну точку перегиба для или и один минимум для .

В последнем случае потенциальная функция есть и потому этот минимум более сложный с математической точки зрения, чем предыдущие. Здесь равны нулю первые три производные функции , тогда как во всех остальных случаях равна нулю только первая производная. Это отвечает трем совпадающим корням кубики для .

Отметим также, в чем состоит различие между потенциальными функциями точек , лежащих на ветвях и : для точка перегиба лежит слева от минимума, а для – справа (рисунок 1.28).

А б

Рисунок 1.28 - Возможные критические точки

потенциальной функции – а, и ее вид – б

С точки зрения динамики минимумы 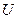отвечают устойчивым равновесиям, а максимумы или перегибы – неустойчивым. Итак, если наша пара управляющих параметров лежит в , то имеется единственное положение устойчивого равновесия, а если в 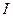, то имеются два устойчивых положения и одно неустойчивое.

Это довольно сложное поведение потенциальной функции можно охватить единой геометрической картинкой, делающей всё чрезвычайно наглядным, нарисовав многообразие катастрофы, или поверхность равновесия, в пространстве .

Это – множество точек , удовлетворяющих уравнению, которое мы здесь перепишем так .

Оно имеет вид поверхности со сборкой и показано на рисунке 1.29.

Рисунок 1.29 - Катастрофа складки Машины Зимана и ее отображение

Теперь мы в состоянии дать геометрическую интерпретацию положений равновесия соответствующей динамической системы.

Для данной пары значений параметров положения равновесия получаются решением уравнения (7.2). Они могут быть, следовательно, описаны как 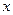-координаты тех точек, в которых вертикальная прямая, проходящая через , пересекает многообразие катастрофы.

Геометрически очевидно, что если лежит в области , внешней по отношению к бифуркационному множеству , то найдется лишь одно такое 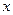; действительно, над точками лежит лишь один лист поверхности.

В то же время над точками области 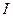расположены три листа и соответственно имеется три положения равновесия.

Для точки вертикальная прямая, проходящая через , касательна к нижнему листу и проходит через верхний лист в единственной точке; это дает для уравнения (7.2) два совпадающих корня и еще один, причем совпадающие корни меньше.

Для всё аналогично, только теперь имеет место касание верхнего листа и совпадающие корни больше. Наконец, в точке острия 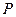вертикальная прямая касается поверхности и пересекает ее в одной-единственной точке – в начале.

Итак, при геометрическом описании состояний равновесия почти всё становится совершенно очевидным. Чтобы закончить картину, необходимо только различить устойчивые и неустойчивые положения равновесия. Неустойчивые отвечают точкам поверхности, лежащим на среднем листе, внутри кривой складок. Устойчивые – точкам снаружи кривой складок.