Броундық қозғалыс кездейсоқ процесс ретінде

Математикалық статистиканың негізгі түсініктері

Математикалық статистика бақылау барысында алынған статистикалық мәліметтерге негізделген көптеген кездейсоқ жағдайларға тәуелді заңдылықтарды орнатады. Математикалық статистиканың негізгі екі міндеті бар:

- Берілген статистикалық мәліметтерді жинау және топтау әдістерін анықтау;

- зерттеудің мақсатына байланысты алынған мәліметтерді сараптаудың әдістерін құрастыру.

Математикалық статистиканың негізгі түсініктері:

Негізгі жиынтық – барлық объектілердің саны;

Сұрыптау –негізгі жиынтықтан кездейсоқ іріктелген объекттер жиынтығы;

N негізгі жиынтықтың көлемі мен и n сұрыптау көлемі– берілген жиынтықтағы обьекттер саны.

Сұрыптау түрлері:

Қайталанбалы – әрбір таңдалынған объект келесі объектті таңдар алдында жалпы жиынтыққа қайтады;

Қайталанбайтын– таңдалынған объект жалпы жиынтыққа оралмайды;

Ескерту. Негізігі жиынтықтың бізге керекті белгісінің мінезі туралы сұрыптау зерттеуі арқылы қорытынды жасау үшін, сұрыптау негізгі жиынтықтың пропорциясын дұрыс анықтауы қажет, яғни репрезентативті болуы керек.Үлкен сандар заңын ескере отырып, бұл шарт әрбір объект кездейсоқ таңдалса орындалады деп есептеуге болады және барлық объекттердің сұрыптауға түсу ықтималдылығы тең.

Броундық қозғалыс

Бро́ундық қозғалыс — сұйық немесе газдың ішіндегі микроскопиялы көрінетін және өлшенетін бөлшектредің газ немесе сұйықтың жылулық қозғалысы есебінен ретсіз қозғалысы. Бұл қозғалыс ешқашан тоқтамайды. Броундық қозғалыс жылулық қозғалыспен байланысты, бірақ бір ұғым емес. Броундық қозғалыс жылулық қозғалыстың дәлелдемесі де нәтижесі.

Броундық қозғалыс атомдар мен молекулалардың бей-берекет жылулық қозғалысы жөніндегі молекула-кинетикалық теорияның ең көрнекті дәлелі болып есептеледі. Егер бақылау уақыты (t) жеткілікті ұзақ болса және орта молекулаларының бөлшекке әсер ету күші өзінің бағытын бірнеше рет өзгертсе (сыртқы күш әсер етпеген жағдайда),

Классикалық теорияның құрылымы

1905 жылы Альберт Эйнштейн броундық қозғалысты сандық жағынан сипаттайтын молекула-кинетикалық теория ұсынды. Дәлірек айтсақ, ол сфералық броундық бөлшектердің диффузия коэффициентін анықтайтын формула тапты:

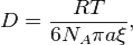
Мұндағы 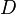— диффузия коэффициенті, 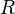— газдың универсалды тұрақтысы, 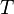— абсолют температура, 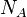— Авогадро тұрақтысы, 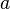— бөлшек радиусы, 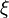— динамикалық тұтқырлық.

Броундық қозғалыс кездейсоқ процесс ретінде

Соңғы ғасырда жақсы дамуға жеткен броундық қозғалыс болжамды шама. Көптеген практикалық жағдайларды бұл теория қанағаттандырғанымен, кейбір оқиғаларда нақтырақ дәлел қажет етеді. Осыған байланысты С.Дженей бастамасымен ХХІ ғасыр басында Лозанна Аолитехникалық университетінде, Техас және Еуропалық молекула-биологиялық лабороторияларда өткізілген тәжірибелер броундық қозғалыс пен Эйнштейн – Смуховскийдің теориялық қозғалысынан өзгешелігін көрсетті. Бұл өзгеріс бөлшектерді ұлғайтқанда анығырақ көрінді. Бұл зерттеуде тағы қоршаған орта бөлшектерінің қозғалысының анализі өткізіліп, олардың броундық бөлшектерге әсері байқалды. Және де жұрілген қозғалыс күінің болашақ қозғалысқа әсері бар екені анықталды. Бұл әсер Эйнштейн – Смолуховский теориясында ескерілмеді.