Пример построения границы Д-разбиения и выделений области устойчивости для системы регулирования турбины, работающей в электрическую сеть

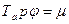-уравнение ротора; (5-17)

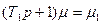-уравнение главного усилителя; (5-18)

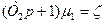-уравнение промежуточного усилителя; (5-19)

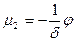-уравнение регулятора скорости. (5-20)

Здесь 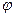- относительная частота вращения ротора турбины,

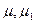–относительные величины перемещения поршней сервомоторов усилителей системы регулирования турбины;

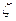-относительная величина перемещения муфты регулятора скорости;

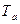-динамическая постоянная ротора турбины;

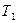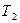и - времена сервомоторов;

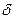- коэффициент неравномерности регулятора скорости.

; ; .

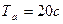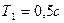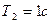Параметром настройки регулятора скорости является коэффициент .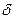

Необходимо определить возможный диапазон изменения коэффициента неравномерности 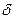, значения которого обеспечивали бы устойчивый процесс регулирования турбины.

Применим метод Д-разбиения для определения границы устойчивости работы АСР турбины по отношению к настроечному параметру 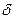. Обозначим .

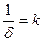Характеристическое уравнение АСР турбины в общем виде:

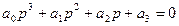, (5-21)

где ; ; ; .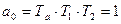

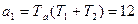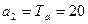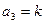Решим характеристическое уравнение относительно .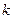

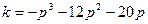(5-22)

Заменим ,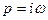

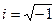
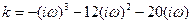(5-23)

Выделим в этом уравнении вещественную и мнимую составляющие: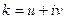

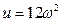-вещественная составляющая

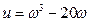-мнимая составляющая

Построим границу Д-разбиения в комплексной плоскости 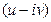, задаваясь значениями в диапазоне от -∞ до ∞.

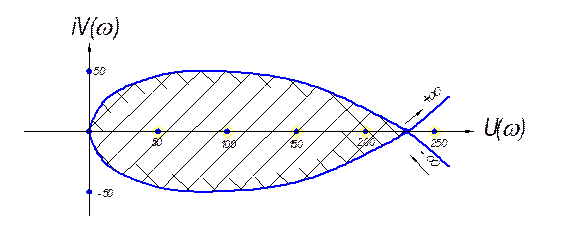
Рис. 5.8 Построение границы устойчивости.

В результате построения границы Д-разбиения получают на вещественной оси комплексной плоскости 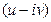две граничные точки параметра k: 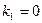, 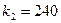или при 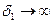, а 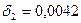(Рис. 5.8).

Поскольку в плоскости корней характеристического уравнения область устойчивости находится слева от мнимой оси плоскости корней, то при движении вдоль границы Д-разбиения в сторону возрастания , область устойчивости располагается так же слева. Штриховкой определяем эту область. Следовательно устойчивая работа АСР турбины возможна при значениях коэффициента неравномерности 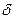при его значениях больше 0,0042.

Для построения области устойчивости по двум параметрам в характеристическое уравнение подставляют 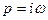и после разделения действительной и мнимой его части получают систему двух уравнений, определяющую кривую Д-разбиения. Если эти уравнения совместны, т.е если их совместное решение не приводит к противоречивому результату и линейно независимы (не равносильны), то каждому значению соответствует одна пара неизвестных значений параметров и, следовательно, одна точка на плоскости.

При некоторых значениях уравнения могут стать равносильными. В этом случае для данного значения получается не точка, а кривая или прямая, которая называется особой. Обычно особые прямые появляются при значениях 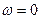и 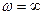, что соответствует переходу корня характеристического уравнения из левой части плоскости корней в правую ее часть через значение нуль или бесконечность. Особая прямая, соответствующая обращения корня в нуль, определяется из условия равенства нулю свободного члена характеристического уравнения. Особая прямая, соответствующая обращению корня в бесконечность, получается при приравнивании нулю коэффициента при старшем члене характеристического уравнения.

Построив основную кривую Д-разбиения и дополнив ее особыми прямыми, находят область устойчивости, используя правила штриховки для ее определения, путем проверки соблюдения условий устойчивости для такой точки, находящейся внутри устойчивого регулирования, для которой вычисления производятся наиболее просто.

Правила штриховки границы Д-разбиения и определения области устойчивости.Если главный определитель полученной системы уравнений больше нуля, то при изменении от -∞ до ∞ штрихуется левая сторона кривой, если главный определитель меньше нуля, то следует штриховать правую сторону кривой Д-разбиения.

Особые прямые штрихуются так, чтобы вблизи точек пересечения их с основной кривой Д-разбиения штриховка была направлена согласно со штриховкой основной кривой. Если при переходе через точку пересечения знак главного определителя меняется, то направление штриховки особой прямой по обе стороны от точки пересечения различно. Если знак главного определителя не меняется, то особую прямую можно не штриховать, так как она является граничной.

Конструктивные и настроечные параметры системы должны обеспечивать достаточный запас устойчивости в ее работе. Чем дальше от поверхности или кривой, ограничивающих область устойчивости, находится рассматриваемая точка, тем большим запасом устойчивости обладает система.