Системы дифференциальных уравнений
Определение6.4.3.Нормальной системой дифференциальных уравнений называется система вида
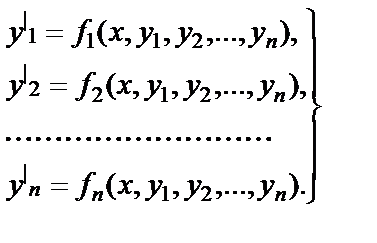 (6.4.42)
(6.4.42)
Здесь число уравнений равно числу неизвестных функций.
Решением системы (6.4.42) называется совокупность n функций 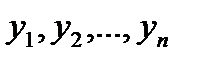 , удовлетворяющих всем уравнениям системы.
, удовлетворяющих всем уравнениям системы.
Частным решением системы (6.4.42.) называется решение, удовлетворяющее начальным условиям:
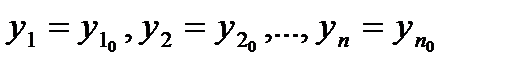 при x=x0,
при x=x0,
где x0, 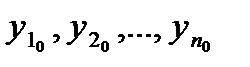 - заданные числа.
- заданные числа.
Семейство решений системы (6.4.42), зависящее от n произвольных независимых постоянных 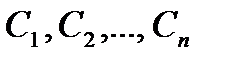 :
:
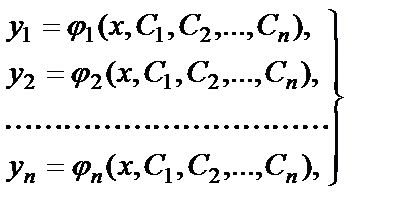
называют обычно общим решением этой системы.
6.5.Теория вероятности
Основные формулы и теоремы.
Классическое определение вероятности
Вероятность события А обозначается символом р или р(А). При классическом определении вероятность события А равна
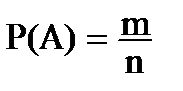 (6.5.1)
(6.5.1)
Отношению числа случаев m , благоприятствующих ему из общего числа n равновозможных, единственно возможных и несовместных случаев, к числу n , т.е.очевидно, что число 0 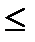 P (А)
P (А) 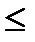 1.
1.
Задача 6.5.1.
По телевидению передано 10 снимков, из них три снимка с искажениями. Какова вероятность, что два взятых на удачу снимка: а) не имеют искажений б) оба имеют искажения? в) один имеет искажение?
Решение:Два снимка из десяти можно выбрать n= 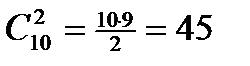 способами (порядок не важен). Обозначим события: а) Событие А- оба снимка не .имеют искажения т.е. они выбраны из 7 качественных снимков. Это можно сделать
способами (порядок не важен). Обозначим события: а) Событие А- оба снимка не .имеют искажения т.е. они выбраны из 7 качественных снимков. Это можно сделать 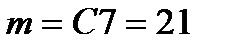 способами. Следовательно,
способами. Следовательно, 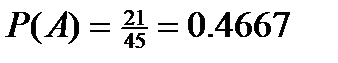 .б) Событие В - оба снимка имёю искажения, т.е. они взяты .из трех некачественных . Получим
.б) Событие В - оба снимка имёю искажения, т.е. они взяты .из трех некачественных . Получим 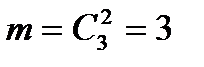 , откуда
, откуда 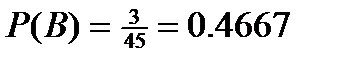 . в) Событие С - один имеет искажение и один не имеет искажение, т.е. один снимок взят из 3 , а 1 - из 7. По правилу произведения это можно сделать
. в) Событие С - один имеет искажение и один не имеет искажение, т.е. один снимок взят из 3 , а 1 - из 7. По правилу произведения это можно сделать 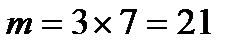 способами, поэтому
способами, поэтому 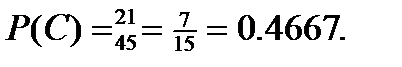
Задача 6.5.2
а)Сколько различных трехзначных чисел можно записать при помощи цифр 1; 2? б)Найти вероятность, что записано число 121. (Событие А).
Решение: а) Трехзначные числа - упорядоченные тройки элементов, образованные из цифр 1 и 2, размещения с повторениями из двух элементов по 3. Их число 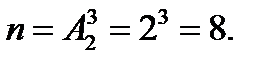 б) Событию А благоприятствует один исход m=1. Поэтому
б) Событию А благоприятствует один исход m=1. Поэтому 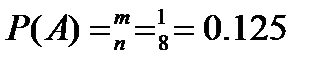 .
.
Теоремы сложения и умножения вероятностей
Непосредственный подсчет вероятности, основанный на построении полной группы событий, практически редко может быть осуществлен. Поэтому основной задачей теории является рассмотрение различных теорем, с помощью которых вероятности одних событий определяются по вероятностям других событий. Важнейшие из них - теоремы сложения и умножения. Условная вероятность события А относительно события В равна:
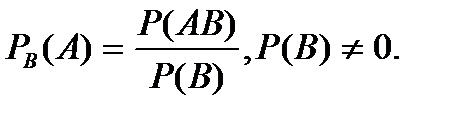
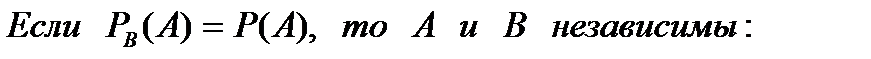
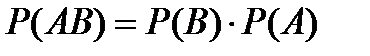 (6.5.1)
(6.5.1)
Выражение (6.5.1) получило название теоремы умножения вероятностей.
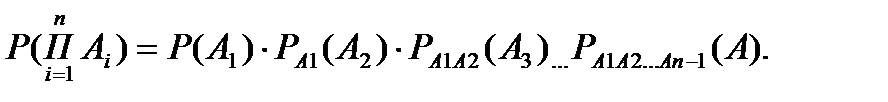 В случае произведения более чем двух событий теорема умножения вероятностей принимает вид
В случае произведения более чем двух событий теорема умножения вероятностей принимает вид
События 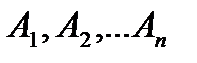 независимы в
независимы в  совокупности, если
совокупности, если 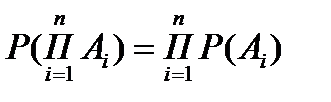 (6.5.2)
(6.5.2)
Теорема сложения вероятностей: если 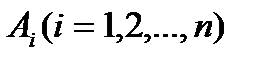 события попарно несовместимы, то вероятность суммы событий равна сумме вероятностей этих событий:
события попарно несовместимы, то вероятность суммы событий равна сумме вероятностей этих событий:
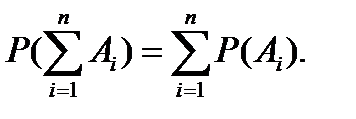 (6.5.3.)
(6.5.3.)
Если несовместные события образуют полную группу, то сумма вероятностей этих событий равна 1. В частности, для двух, противоположных событий Аи имеет место равенство
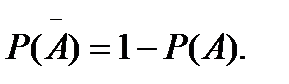
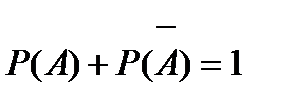 , и поэтому вероятность противоположного события вычисляется по формуле
, и поэтому вероятность противоположного события вычисляется по формуле
Если события совместны, то формулы для вероятности суммы этих событий усложняются. Например, вероятность суммы двух местных событий равна
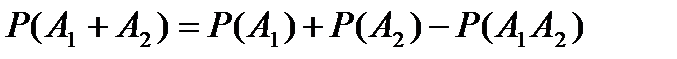 ,
,
а вероятность суммы трех совместных событий
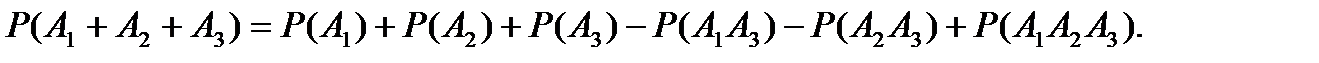
Задача 6.5.3.
Из коробки, содержащей 5 красных и 3 черных шариковых ручки, извлекают 2 ручки. Найти вероятность того, что: а) обе ручки красные. 6) ручки разных цветов. Рассмотреть 2 случая: 1) извлеченная первой ручка не возвращается в коробку; 2) извлеченная первой ручка возвращается в коробку перед извлечением второй.
Решение. Введём обозначения для событий: А - обе ручки красного цвета;В - ручки разных цветов. Следует определить Р(А) и Р(В)
Введём события, связанные с извлечением одной ручки: А1-первая ручка: красная; 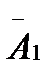 - первая ручка чёрная, А2 - вторая ручка красная;
- первая ручка чёрная, А2 - вторая ручка красная; 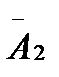 вторая ручка черная. Тогда
вторая ручка черная. Тогда 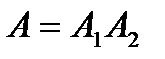 и
и 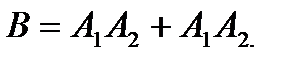 .
.
Применяем формулы (6.5.1) и (6.5.3).
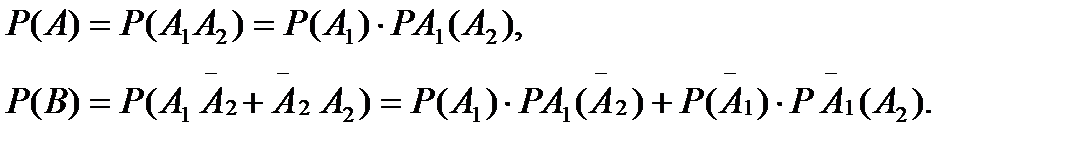
В данном случае события 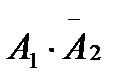 и
и 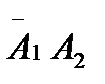 несовместны.
несовместны.
1 случай. 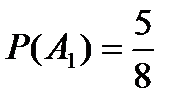 Так как после наступления
Так как после наступления 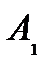 ручка не возвращается, то в коробке окажется 7 ручек. Из которых 4 красных и поэтому
ручка не возвращается, то в коробке окажется 7 ручек. Из которых 4 красных и поэтому
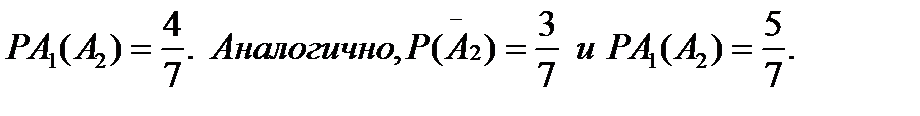
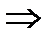
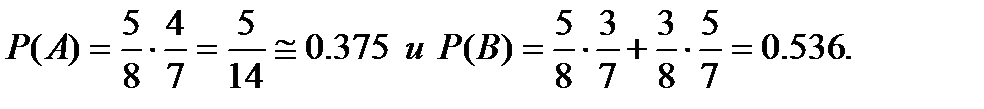
2 случай. 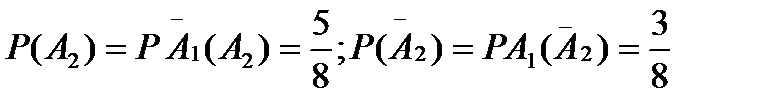 (так как после наступления
(так как после наступления 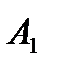 ручка возвращена в коробку).
ручка возвращена в коробку).
а) 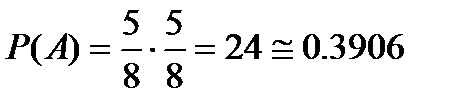 . б)
. б) 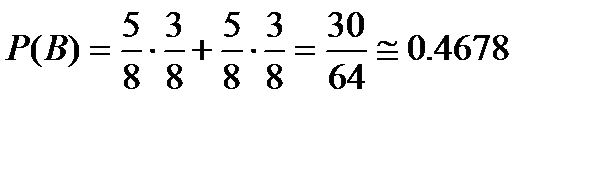 . Задача 6.5.4
. Задача 6.5.4
Прибор собирается последовательно четырьмя рабочими. Независимо от остальных 1-й может допустить брак вероятностью 0,1,2-й и 3-й - с вероятностью 0,09, а 4-й -0,15. Готовый прибор относится к I сорту, если ни один рабочий не допустил брак, ко II, если брак допущен 2-м или 3-м рабочим, к III сорту, если брак допустили 1 -й или 4-й рабочие и признаётся негодным в остальных случаях. Найти вероятности следующих событий:А - прибор признан I сорта; В - II сорта; С - Ш сорта; D - прибор признан негодным.
Решение: Обозначим Через Аi событие, состоящее в том, что i-ый рабочий не допустил брак, тогда 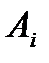 -i-ый рабочий допустил брак i=1,2,3,4 . В условии дано Р(А1) =01; Р(А2)= Р(АЗ)=0,09 ; Р(А4)=0,15. Тогда P(A1)=0.9; P(A2)=P(A3)=0.91; Р(A4) = 0.85
-i-ый рабочий допустил брак i=1,2,3,4 . В условии дано Р(А1) =01; Р(А2)= Р(АЗ)=0,09 ; Р(А4)=0,15. Тогда P(A1)=0.9; P(A2)=P(A3)=0.91; Р(A4) = 0.85
Интересующие нас события можно представить следующим образом: A=A1А2А3А4; B=A1A2A3A4+ 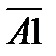 А2А3А4;C=A1A2A3A4+
А2А3А4;C=A1A2A3A4+ 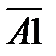 A2A3А4. Событие D противоположно сумме событий А+В+С, т.е. D= A+B+C:
A2A3А4. Событие D противоположно сумме событий А+В+С, т.е. D= A+B+C:
Применяем формулы (6.5.2) для независимых событий и (6.5.3) для несовместных событий-слагаемых в выражениях для В и С, получим
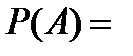
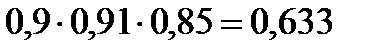
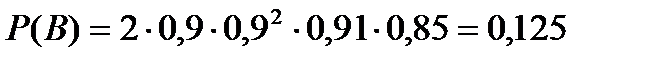
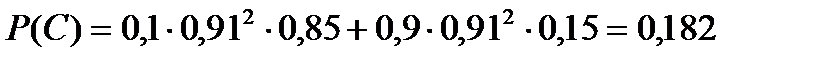
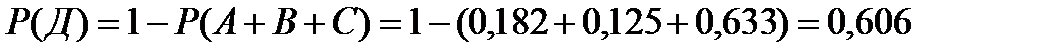
Задача 6.5.5
Вероятность того, что проходящая машина потребует заправки в данном пункте, равна 0.3. Сколько должно пройти машин чтобы с вероятностью не меньшей, чем 0.9 можно было утверждать, что хотя бы одна потребует заправки?
Решение: Введем обозначения для событий : Аi –i-я машина потребует заправки и С - хотя бы одна машина из и потребует заправка. Тогда С=А1+А2+...+Аn.
Однако все слагаемые совместны, поэтому перейден противоположному событию С -“ни одна машина из n потребует заправки” получим
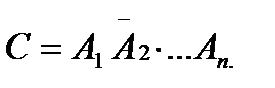
События A1 ,А2,..., An , а следовательно , _ A1 А2…Аn независимы и имеют одну и ту же вероятность 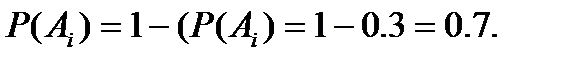
Поэтому 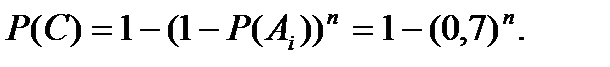 По условию задачи
По условию задачи 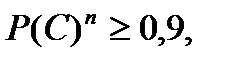 те.
те. 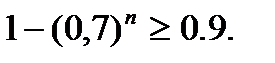 Решая это неравенство, найдем последовательно
Решая это неравенство, найдем последовательно 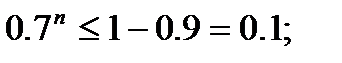 n lg 0.7
n lg 0.7 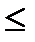 lg 0,1, откуда
lg 0,1, откуда 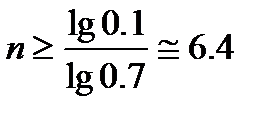 . Окончательно получаем n=7.
. Окончательно получаем n=7.
Формула полной вероятности. Формула Бейеса
Из теорем сложения и умножения получается формула полной вероятности и формула Бейеса. Если события A1, A2,...,An образуют полную группу (гипотезы) и событие А, то может произойти вместе с одним из событий А, тогда
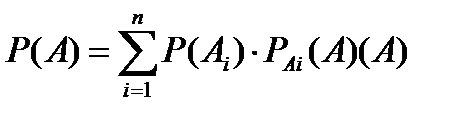 - формула полной вероятности .
- формула полной вероятности .
Если же в результате проведения опыта зафиксировано появление события А, то переоценка вероятности гипотез равна
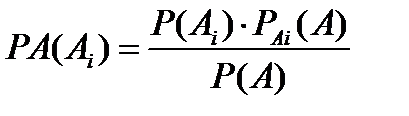 - формула Бейеса.
- формула Бейеса.
Задача 6.5.6
Известно, что в партии из 600 электрических лампочек 200 изготовлены на первом заводе, 250 на втором заводе и 150 на третьем заводе. Известны также вероятности 0.97, 0.91 и 0.93 того, что лампочка окажется стандартно о качества при изготовлении ее соответственно 1,2,3 заводами. Какова вероятность, что на удачу выбранная из данной партии лампочка окажется стандартной.
Решение: Обозначим через А событие, состоящее в том , что лампочка окажется стандартной:
А - лампочка изготовлена на 1 заводе,
А - лампочка изготовлена на 2 заводе,
А - лампочка изготовлена на 3 заводе.
Известно, что РА1(А)=0,97; РА2(А)=0,91;РА3(А)=0,93.
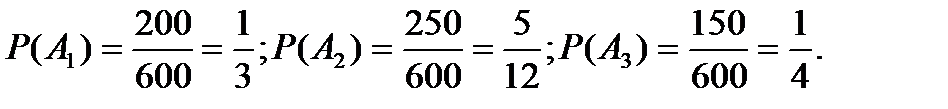
Событие А1,А2,А3 образуют полную группу и по формуле полной вероятности находим
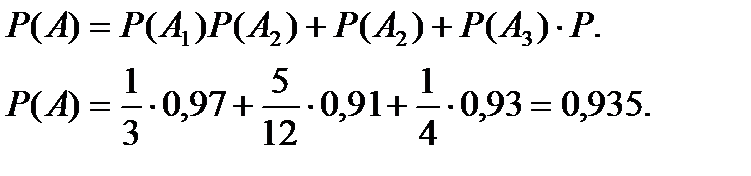
Задача 6.5.7
При массовом производстве некоторого изделия вероятность того, что оно окажется стандартным, равна 0 95. Для контроля производится некоторая упрощенная проверка стандартности изделия, которая дает положительный результат в 99% случаев стандартности изделии и в 3% случаев для нестандартных изделий. Какова вероятность стандартности изделий, выдержавшего упрощенную проверку?
Решение: Введем события;
А1 - изделие окажется стандартным,
А2 - изделиеокажется нестандартным.
А 3 - изделие выдержит упрощеннуюпроверку.
События A1, А2 образуют полную группу. До проверки Р(А1)=095,Р(А2)=0 05. Известно, что РА1(А)=0,99 РА2(А)=0,03. Нас интересует вероятность стандартности издания, прошедшего проверку, т.е РА(А1). По формулам Бейеса получаем
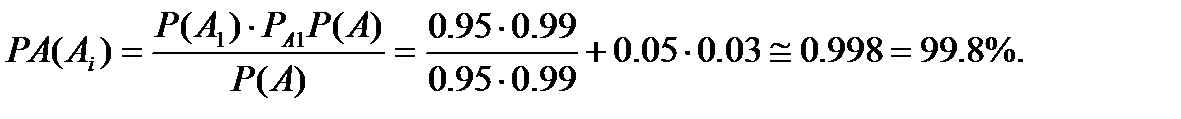
Это означает, что в среднем только 2 изделия из 1000 , успешно прошедших проверку, будут нестандартным.
Схема испытаний Бернулли (повторение опытов)
Вероятность того, что в n независимых испытаниях, в, каждом из которых вероятность появления события равна p(0<p>1), событие наступит ровно m раз (безразлично, в какой последовательности), есть
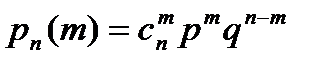 где q=1-p.Вероятность- того, что событие наступит:
где q=1-p.Вероятность- того, что событие наступит:
а) менее m раз: 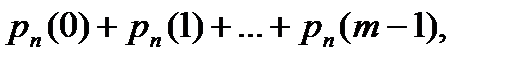
б) более m раз: 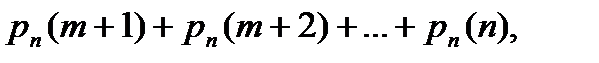
в) не более m раз: 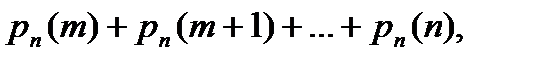
г) не более m раз: 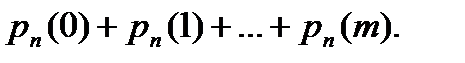
Вероятность наступления события А хотя бы один раз при проведении n независимых испытаний, равна:
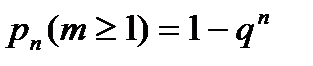 , где
, где 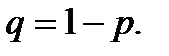
Наивероятнейшее значение 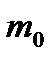 числа наступления события А при проведении n независимых повторных испытаний, вычисляется по формуле
числа наступления события А при проведении n независимых повторных испытаний, вычисляется по формуле 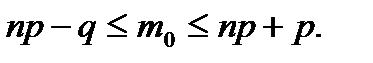
Задача 6.5.8
Вероятность того, что денежный приемник автомата при опускании одной монеты срабатывает правильно, равна 0,97. Сколько нужно опустить монет, чтобы наивероятнейшее число случаев правильной работы автомата было равно 100?
Решение. Двойное неравенство
np-q< 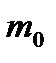 <np+p при p=0.97, q=0,03 и
<np+p при p=0.97, q=0,03 и 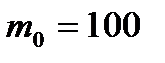 даёт
даёт
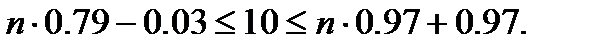
Следовательно, с одной стороны,
0,97n-0.03< 100, откуда 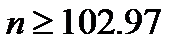
С другой стороны
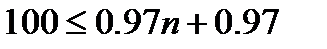 откуда n
откуда n 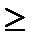 302.09 т.е. 102,09
302.09 т.е. 102,09 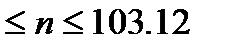 .
.
Поэтому n= 103 , как то целое число которое заключено между 102,09 и 103.12.
Предельные теоремы
Если число испытаний n велико , то применение формулы Бернулли приводит к громоздким вычислениям . В таких случаях пользуются предельными теоремами Лапласа. а) Локальная теорема Лапласа. Вероятность того, что в n независимых испытаниях, в каждом из которые вероятность появления события равна р(о<р < 1), событие наступит ровно m раз, выражается приближенным равенством
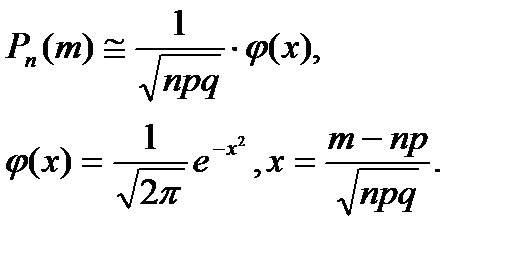
Функция у(х) - четная, т.е. у(-х)= γ(х). При х>5 можно считать, что γ(x)=0. б) интегральная теорема Лапласа. Вероятность того, что в n, независимых испытаниях, в каждом из которых вероятность появления. события равна р, событие наступит не менее m1 раз и не более m2 раз, выражается приближенным равенствам
При 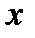 >5 полагают Ф(х)=5. Функция Лапласа – нечетная, т.е.
>5 полагают Ф(х)=5. Функция Лапласа – нечетная, т.е.
Ф(-х)=-Ф(х), Ф(0)=0.
Если число испытаний достаточно велико , а р - мало при, этом 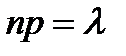 не больше 10 (
не больше 10 ( 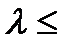 10), то вероятность
10), то вероятность 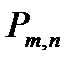 можно найти приближенно по формуле Пуассона:
можно найти приближенно по формуле Пуассона: 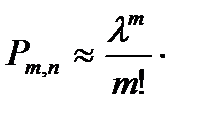
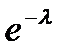 .
.
Задача 6.5.9
Прибор состоят из 200 деталей, каждая из которых за врем tможет выйти из строя с вероятностью р=0 01. Найти вероятность того, что за время t выйдут из строя: а) 3 детали; б) не более 3 деталей; г) от двух до четырех деталей включительно.
Решение: В данном случае n=200, m=0.01, q=0.99, m- количество
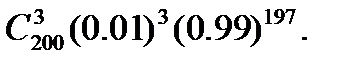 деталей ,
деталей ,
вышедших аз строя за время t. а) m=3;РЗ;200 по формуле Бернулли равно
| Оценим значение |
Практически формула непригодна для вычисления. Найдем np=200 0.01=2, меньше 10 Можно использовать формулу Пуассона при X = 2 и m=3; сразу получаем Р3,200 =0.1805; б) 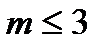 - не более 3 деталей вышло из строя
- не более 3 деталей вышло из строя
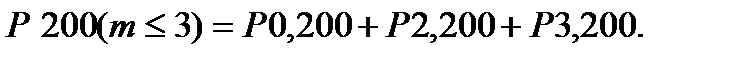 Для вычисления каждого слагаемого используем формулу Пуассона, определяя значения вероятностей по таблице при
Для вычисления каждого слагаемого используем формулу Пуассона, определяя значения вероятностей по таблице при 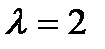 и при m=0,1, 2,3.
и при m=0,1, 2,3.
Р200( 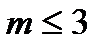 ) = 0.8572;
) = 0.8572;
в){т > 2}- не менее двух деталей вышло из строя .Здесь следует перейти к противоположному событию m<2. Тогда Р200(m>2)=1-Р0,2ОО –P1,200=0.5940.
г)2< m <1 от двух до четырех деталей включительно за время t вышли из строя следует найти Р200(2<m< 4)=Р2,200+Р3,200+Р4,200. Используя, формулу Пуассона опять при 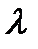 =2 и m=2,3,4 по таблице находим
=2 и m=2,3,4 по таблице находим
Р200 
Задача 6.5.10
Вероятность изделию быть, бракованным равна 0.05. Найти вероятность того, что среди 1000 изделий а) 40 бракованных; б) число бракованных находится впромежутке от 40 до 70 включительно; в) сколько изделий надо взять, чтобы с вероятностью, не менее 0,9 среди них оказалось не менее 50 бракованных?
Решение: Испытание изделий на брак удовлетворяет модели испытаний Бернулли Вероятность для каждого изделия быть бракованным, р=0.05, а набракованным q=0.95. Испытаниям подвергаются n=1000 изделий.
a) m=40; Р 40,1000 находим по формуле Муавра Лапласа. Определим необходимые величины: np=50; npq=47,5, 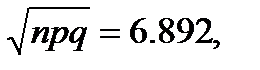
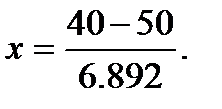
f(-1.45)=f(1.45)=0.1392.Окончательно получаем 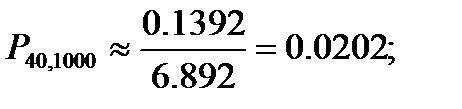
б) Р1000 (40< m < 70) находим по интегральной формуле Муавра –Лапласа при 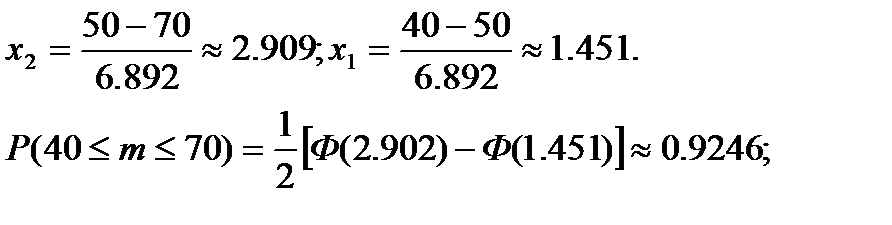
в) необходимо найти число n,удовлетворяющее условию
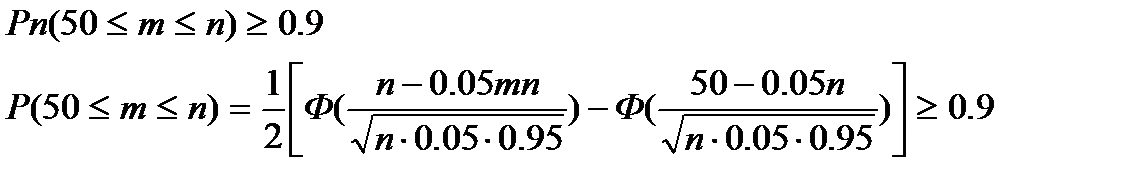
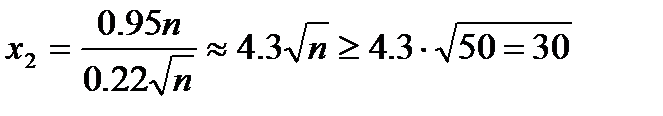
(Очевидно, что 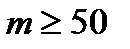 ).Следовательно Ф(x2)=1. Получаем
).Следовательно Ф(x2)=1. Получаем
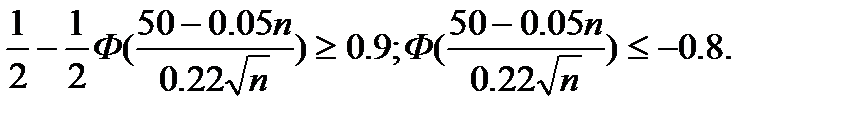
По таблице, что Ф(t)=-0,8 при t=-1,29. Поэтому 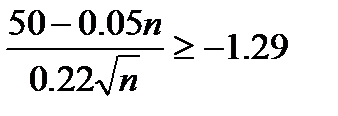 и после упрощения получаем
и после упрощения получаем 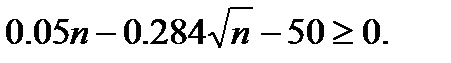 Решив это неравенство, найдем
Решив это неравенство, найдем 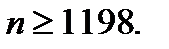 Следует взять менее 1198 изделий.
Следует взять менее 1198 изделий.
Функция распределения случайной величины. Непрерывная случайная величина
Функция распределения F(x) примет значение
F(x)=P(X<x). (6.5.4)
Свойства функции распределения: F(- 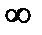 ) = 0; F(+
) = 0; F(+ 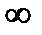 ) = 1. О < F(x) < 1; если х2 >
) = 1. О < F(x) < 1; если х2 > 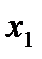 , to F(
, to F( 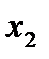 )
) 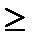 F(
F( 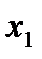 ).
).
Вероятность попадания случайной величины X в промежуток [а;b) определяется формулой
P(a<X<b) = F(b)-F{a). (6.5.5)
Существуют случайные величины, множество значений которых непрерывно заполняют некоторый числовой промежуток.
Если функция F(x) распределения случайной величины X непрерывна и имеет почти всюду (кроме, возможно, конечного числа точек) непрерывную производную, то случайную величину X называют непрерывной,а функцию f(x) = F'(x) называют плотностью вероятности случайной величины X. Имеют место формулы:
а) 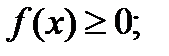 б)
б) 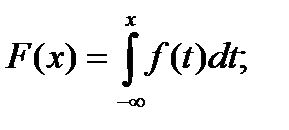
в) 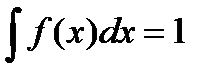 ; г)
; г) 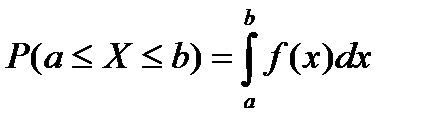 .
.
Вероятность того, что непрерывная случайная величина имеет конкретное значение, равна нулю.
Математическим ожиданием непрерывной случайной величины X называется число M(X), равное
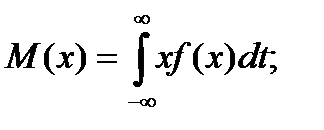 (6.5.6)
(6.5.6)
Дисперсия D(x) непрерывной случайной величины
X определяется по формуле
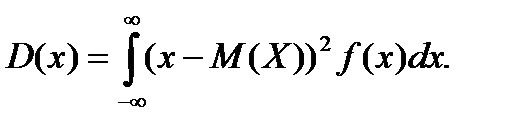 (6.5.7)
(6.5.7)
Задача 6.5.11
Прибор состоит из двух блоков, вероятность безотказной работы каждого из которых в течение времени 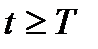 равна 0,5. Найти ряд распределения для числа блоков, работающих, и момент t=T . Найти функцию распределения F(x) ДСВ X
равна 0,5. Найти ряд распределения для числа блоков, работающих, и момент t=T . Найти функцию распределения F(x) ДСВ X
Решение.Обозначим состояние каждого блока через (R) или (О), в зависимости от того, работает он или отказал. Вероятность F(R)=P(O)=1/2. Множество всех исходов опыта Е содержит 4 элемента, вероятность каждого равна ¼, Е = {(0,0); (0,R); (R,0); (R,R)}- Случайная величина X- число работающих блоков к моменту t. Случаю (О О) соответствует значение X=0 (оба блока отказали), 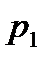 = Р(Х = 0) = 1/4, случаям (О R) и (R О) соответствует значение Х=1 (один блок отказал),
= Р(Х = 0) = 1/4, случаям (О R) и (R О) соответствует значение Х=1 (один блок отказал), 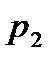 = Р(X = 1)=1/4+1/4=1/2. Случаю (R R) соответствует значение Х=2 (оба блока работают) ,
= Р(X = 1)=1/4+1/4=1/2. Случаю (R R) соответствует значение Х=2 (оба блока работают) , 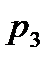 = Р(Х = 2) =1/4.Ряд распределения для случайной величины Х- числа работающих блоков имеет вид
= Р(Х = 2) =1/4.Ряд распределения для случайной величины Х- числа работающих блоков имеет вид
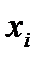 | 0 | 1 | 2 |
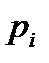 | 1/4 | 1/2 | 1/4 |
Если x 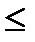 0, то F(x)=0, так как нет ни одного значения X левее нуля.
0, то F(x)=0, так как нет ни одного значения X левее нуля.
Если 0 < x 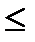 1 ,то в промежуток (-
1 ,то в промежуток (- 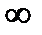 ;0) попадает одно значение Х=0, следовательно, F(x)=P(x=0)=1/4.
;0) попадает одно значение Х=0, следовательно, F(x)=P(x=0)=1/4.
Если 1 < x 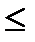 2 ,то в промежуток (-
2 ,то в промежуток (- 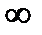 ;х) попадает два значения X =0 и X=1, следовательно, F(x) = Р(Х = 0) + Р(Х = 1) = ¾.
;х) попадает два значения X =0 и X=1, следовательно, F(x) = Р(Х = 0) + Р(Х = 1) = ¾.
Если 2 < x 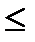
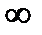 ,то в промежуток (-
,то в промежуток (- 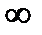 ;x) попадают все значения X, т.е. Х=0, Х=1, Х=2. Следовательно, F(x)=1.
;x) попадают все значения X, т.е. Х=0, Х=1, Х=2. Следовательно, F(x)=1.
Получаем
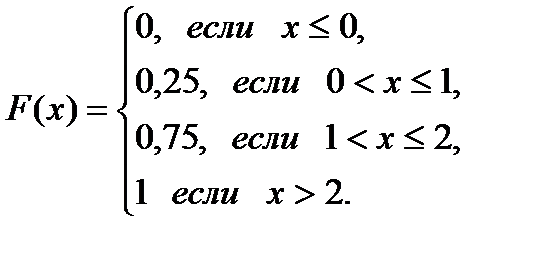
Задача 6.5.12
Составить функцию распределения случайной величины, распределенной по биномиальному закону.
Решение.X принимает значение 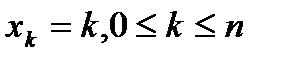 с вероятностями. При
с вероятностями. При 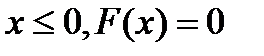 . При
. При 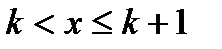 нужно найти сумму значений, попавших в промежуток от -
нужно найти сумму значений, попавших в промежуток от - 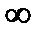 до x, т.е. значения 0,1,2…k.
до x, т.е. значения 0,1,2…k.
Следовательно, 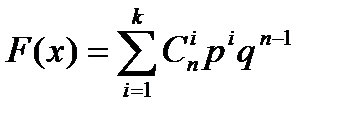 . При x>n, F(x)=1.
. При x>n, F(x)=1.
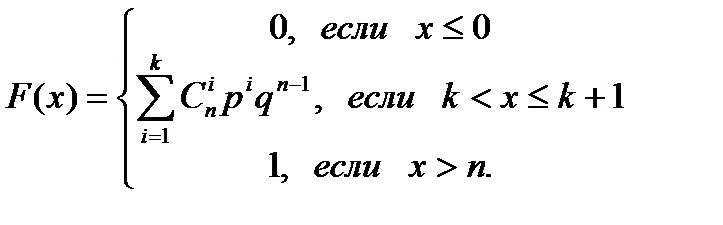
Задача 6.5.13
Случайная величина Х имеет плотность распределения, пропорциональную х при 0 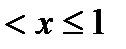 и равную 0 при
и равную 0 при 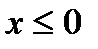 и
и 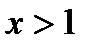 .
.
а) Найти выражение для f(x)
б) Найти М(х), D(x), 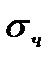 .
.
Решение.а) Выражение плотности распределения имеет вид
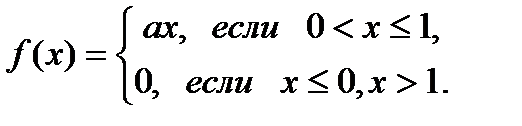
Пользуясь свойством плотности распределения, находим
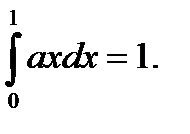
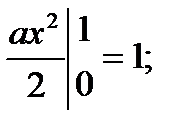 откуда 1/2
откуда 1/2 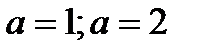
б) Математическое ожидание М(Х)= 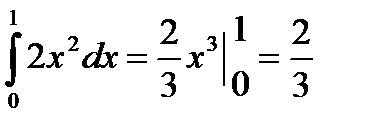
Дисперсия D(X)= 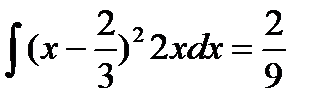
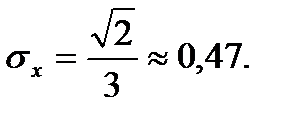
Задача 6.5.14
Задана функция распределения случайной величины X:
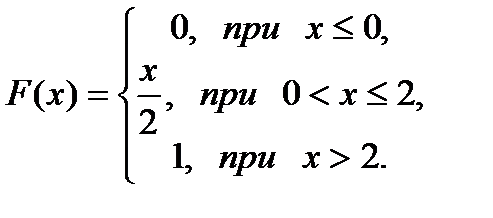
Найти вероятность того, что случайная величина Х примет значение в интервале (1;3).
Решение.Вероятность попадания случайной величины в интервал (1;3) по формуле (1.2) равна P(1<X<3)=F(3)-F(1)=1-1/2=1/2.
Закон больших чисел. Предельные теоремы
Теорема Чебышева 6.5.1Если Х – неотрицательная случайная величина и М(Х) – её математическое ожидание, то для любой А>0 имеет место неравенство
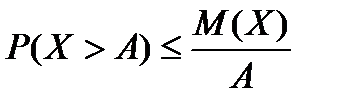 , (6.5.8)
, (6.5.8)
или 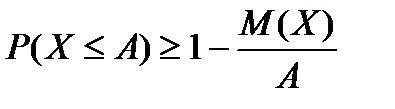 . (6.5.9)
. (6.5.9)
Если случайная величина имеет дисперсию D(X), то для любого 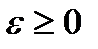 имеет место неравенство Чебышева:
имеет место неравенство Чебышева:
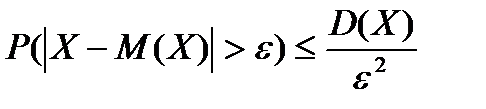 , (6.5.10)
, (6.5.10)
или 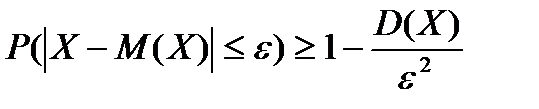 . (6.5.11)
. (6.5.11)
Если 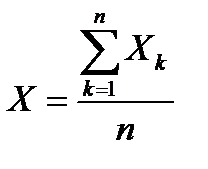 - средняя арифметическая независимых случайных величин
- средняя арифметическая независимых случайных величин 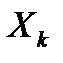 , k=1, … n, каждая из которых имеет
, k=1, … n, каждая из которых имеет 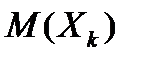 и
и 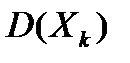 , то неравенство Чебышева принимает вид
, то неравенство Чебышева принимает вид
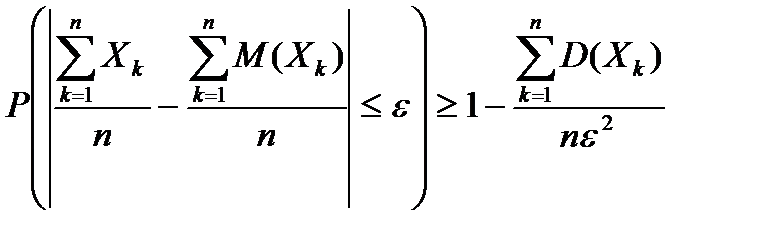 . (6.5.12)
. (6.5.12)
Для случайных величин, одинаково распределённых с 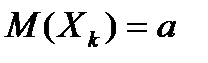 и
и 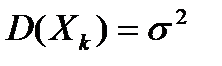 , неравенство (6.5.12) принимает вид
, неравенство (6.5.12) принимает вид
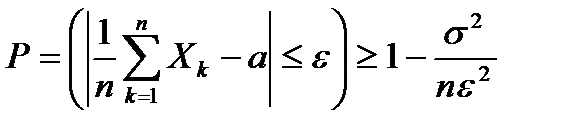 . (6.5.13)
. (6.5.13)
Если дисперсия независимых случайных величин 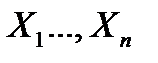 равномерно ограничены числом С, то следствием (6.5.11) является неравенство
равномерно ограничены числом С, то следствием (6.5.11) является неравенство
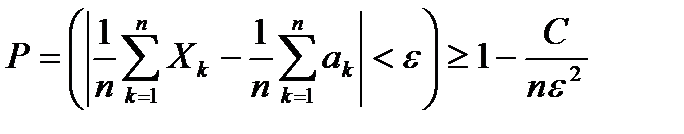 . (6.5.14)
. (6.5.14)
Следствием (6.5.11) является также неравенство Чебышева для случайной величины, распределенной по биноминальному закону:
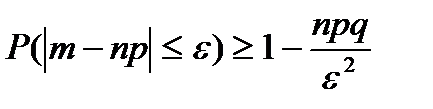 , (6.5.15)
, (6.5.15)
и для случайной величины, равной частности появлений события в n независимых испытаниях:
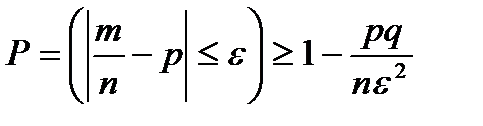 . (6.5.16)
. (6.5.16)
Теорема Ляпунова 6.5.2Пусть дана последовательность независимых случайных величин 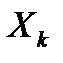 , k=1, … n,…, для каждой из которых существует математическое ожидание
, k=1, … n,…, для каждой из которых существует математическое ожидание 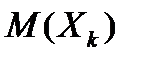 =
= 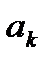 , дисперсия
, дисперсия 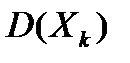 =
= 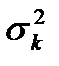 и третий центральный абсолютный момент
и третий центральный абсолютный момент 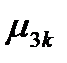 . Если выполняется условие
. Если выполняется условие
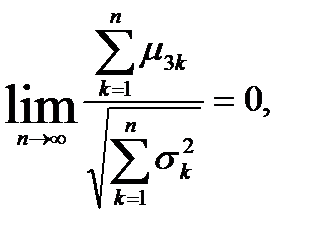 (6.5.17)
(6.5.17)
то случайная величина 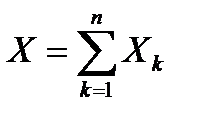 распределена нормально с математическим ожиданием М(Х)=∑
распределена нормально с математическим ожиданием М(Х)=∑ 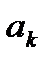 и дисперсией
и дисперсией 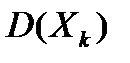 =
= 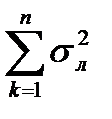 .
.
Теорема Ляпунова относится к группе теорем, объединённых общим названием центральная предельная теорема.Одна из простых формулировок центральной предельной теоремы относится к одинаково распределённым случайным величинам: если 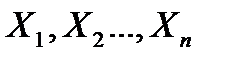 - независимые одинаково распределённые случайные величины с математическими ожиданиями
- независимые одинаково распределённые случайные величины с математическими ожиданиями 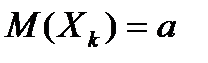 и дисперсиями
и дисперсиями 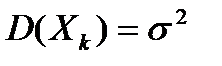 , то при неограниченном увеличении их числа n закон распределения их суммы X приближается к нормальному с параметрами M(X)=na и D(X)=
, то при неограниченном увеличении их числа n закон распределения их суммы X приближается к нормальному с параметрами M(X)=na и D(X)= 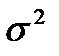 .
.
Теорема Лапласа 6.5.3. Пусть m – частота появлений события A в n независимых испытаниях, а p – вероятность наступления события A в отдельном испытании. При 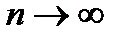 случайная величина
случайная величина 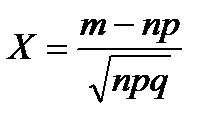 распределена нормально с М(Х)=0 и D(X)=1, то есть
распределена нормально с М(Х)=0 и D(X)=1, то есть
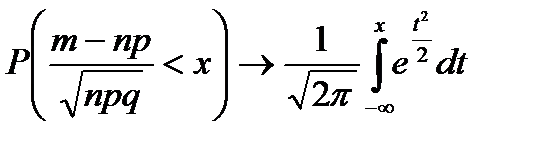 .
.
Приближение формулы Муавра – Лапласа следует из того, что закон распределения случайной величины 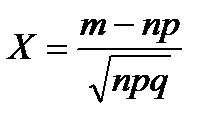 при большом n близок к нормальному с плотностью вероятности
при большом n близок к нормальному с плотностью вероятности 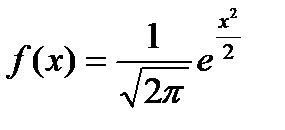 .
.
Задача 6.5.15
Математическое ожидание скорости ветра на аэродроме равно 7 м/с. Оценить вероятность того, что скорость ветра на аэродроме а) не превзойдет 28 м/с : б) будет не менее 35 м/с.
Решение.Случайная величина Х – скорость ветра. а) по условию А – 28 м/с. Применяем неравенство (6.5.12’):
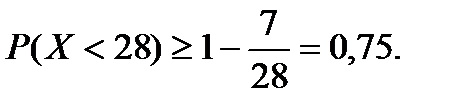
б) По условию А = 35 м/с. Применяем неравенство (6.5.12):
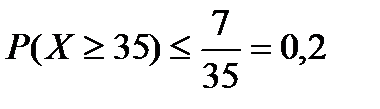 .
.
Задача 6.5.16
Средний вес детали равен 50 г, а дисперсия равна 0,1. Оценить вероятность того, что вес случайно выбранной из партии детали окажется в границах (49,5;50,5).
Решение.Случайная величина Х – вес детали. По условию
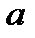 =50 г,
=50 г, 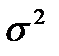 =0,1 и
=0,1 и 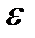 =0,5. Неравенство 49,5<X<50,5 равносильно -0,5<X-50<0,5 , или
=0,5. Неравенство 49,5<X<50,5 равносильно -0,5<X-50<0,5 , или 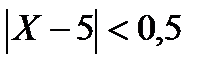 . Поэтому применяем неравенство Чебышева (1.7.2’):
. Поэтому применяем неравенство Чебышева (1.7.2’):
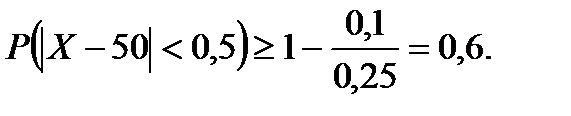
Искомая вероятность не меньше 0,6.
Задача 6.5.17
Сумма всех вкладов в некоторую сберегательную кассу составляет 20000 руб., а вероятность того, что случайно взятый вклад не превышает 100 руб., равна 0,8. Что можно сказать о числе вкладчиков данной сберкассы?
Решение.Пусть Х – размер случайно взятого вклада ,а n – число всех вкладов. Тогда из условия задачи средний размер вклада 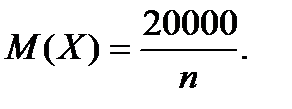 Так как
Так как 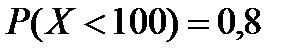 и по неравенству (1.7.1’)
и по неравенству (1.7.1’) 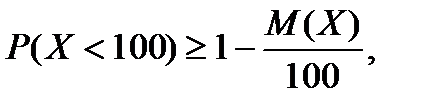 то
то 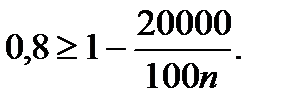 Отсюда
Отсюда 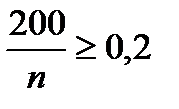 и, следовательно,
и, следовательно, 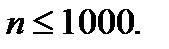
Задача 6.5.18
Ёмкость изготовляемого заводом конденсатора должна быть по техническим условиям равной 2 мкФ с разрешённым допуском 0,1 мкФ. Завод добился средней ёмкости, равной 2 мкФ с дисперсией, равной 0,004 мкФ 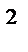 . Какова вероятность изготовления бракованного конденсатора? Расчёт провести по неравенству Чебышева, предположив, что ёмкости конденсаторов распределены по нормальному закону с теми же параметрами.
. Какова вероятность изготовления бракованного конденсатора? Расчёт провести по неравенству Чебышева, предположив, что ёмкости конденсаторов распределены по нормальному закону с теми же параметрами.
Решение.Конденсатор будет бракованным, если отклонение ёмкости конденсатора Х от среднего значения М(Х)=2 мкФ будет по абсолютной величине болеем 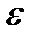 =0,1 мкФ. По неравенству Чебышева (6.5.13 ) имеем
=0,1 мкФ. По неравенству Чебышева (6.5.13 ) имеем
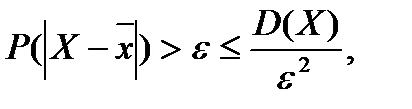 а поэтому вероятность события P
а поэтому вероятность события P 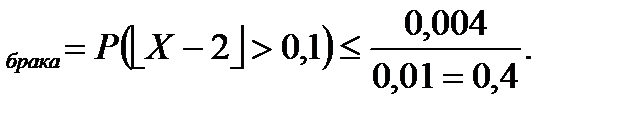
Если же предположить, что значения ёмкости распределены по нормальному закону, то
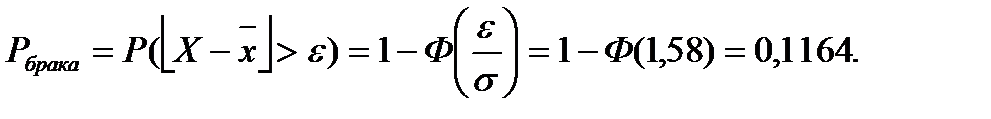
Видим, что, используя значение о нормальном законе распределения, ответ получаем более точным. Неравенство же Чебышева дает грубую оценку, зато оно применимо к случайным величинам, распределенным по любому закону.
Системы случайных величин
Систему двух случайных величин (X,Y) можно изобразить случайно точкой на плоскости.
Событие, состоящее в попадании случайной точки (X;Y) в область D, принято обозначать в виде (X;Y) 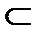 D.
D.
Закон распределения системы непрерывных случайных величин (X,Y) будем задавать с помощью функции плотности вероятности f(x,y).
Вероятность попадания случайной точки (X,Y) в область D определяется равенством
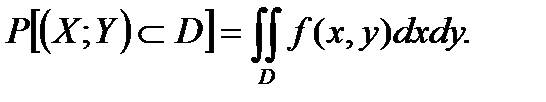
Функция плотности вероятности обладает следующими свойствами:
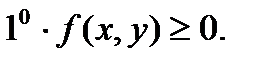
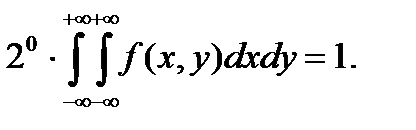
Если все случайные точки (X;Y) принадлежат конечной области D , то последнее условие принимает вид
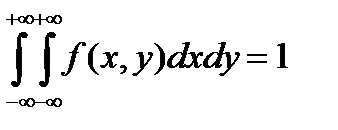 . (6.5.18)
. (6.5.18)
Математическое ожидание дискретных случайных величин X и Y, входящих в систему, определяются по формулам
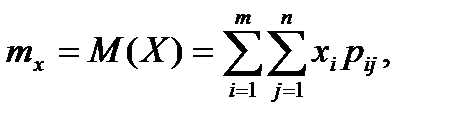
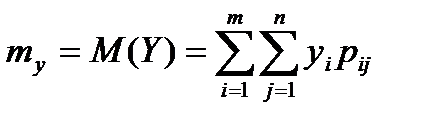 (6.5.19)
(6.5.19)
а математические ожидания непрерывных случайных величии - по формулам
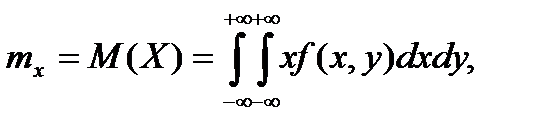 (6.5.20)
(6.5.20)
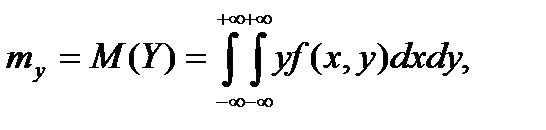 (6.5.21)
(6.5.21)
Точка ( 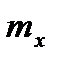 ;
; 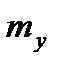 ) называется центром рассеивания системы случайных величин (X,Y).
) называется центром рассеивания системы случайных величин (X,Y).
Математические ожидания 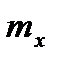 и ту можно найти и проще, если случайные величины X и Y независимы. В этом случае из законов распределения этих случайных величин можно определить математические ожидания
и ту можно найти и проще, если случайные величины X и Y независимы. В этом случае из законов распределения этих случайных величин можно определить математические ожидания 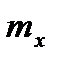 и ту по формуле
и ту по формуле
(6.5.22)
(6.5.23)
Дисперсии дискретных случайных величин X и Y определяются по формулам
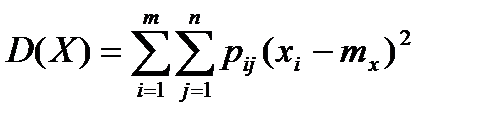 ; (6.5.24)
; (6.5.24)
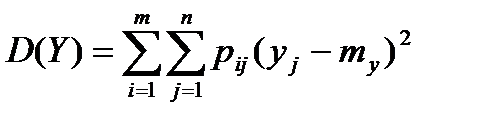 . (6.5.25)
. (6.5.25)
Дисперсии же непрерывных случайных величин X и Y, входящих в систему, находятся по формулам
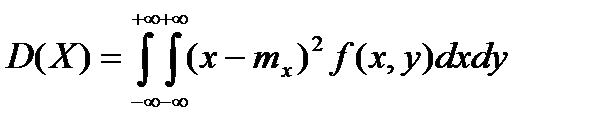 ; (6.5.26)
; (6.5.26)
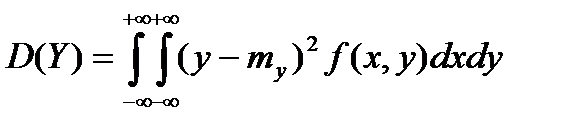 . (6.5.27)
. (6.5.27)
Средние квадратичные отклонения случайных величин X и Y определяются по формулам
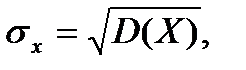
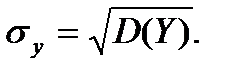 (6.5.28)
(6.5.28)
Для вычисления дисперсий могут быть применены формулы
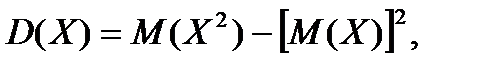
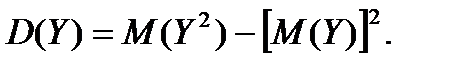 (6.5.29)
(6.5.29)
Важную роль в теории систем случайных величин играет так называемый корреляционный момент (ковариация)
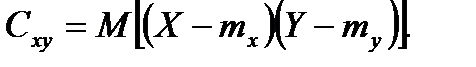 (6.5.30)
(6.5.30)
Для дискретных случайных величин корреляционный момент находится по формуле
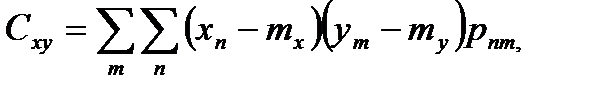 (6.5.31)
(6.5.31)
а для непрерывных – по формуле
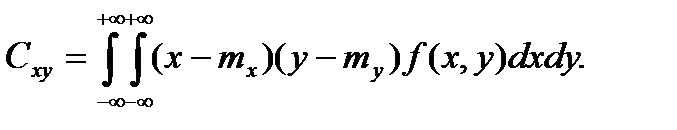 (6.5.32)
(6.5.32)
Корреляционный момент можно также найти по формуле
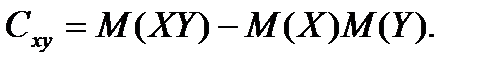 (6.5.33)
(6.5.33)
Здесь
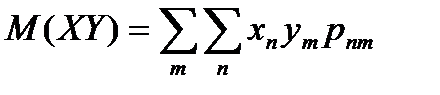
для дискретных величин X и Y и
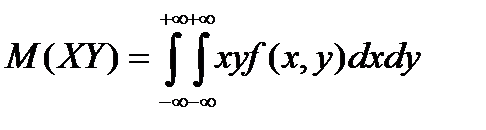 (6.5.34)
(6.5.34)
для непрерывных величин.
Случайные величины X и Y называются независимыми, если вероятность одной из них принимает значение, лежащее в любом промежутке области ее значений, и не зависит от того, какое значение приняла другая величина. В этом случае
M(XY)=M(X)M(Y); 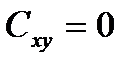
Для характеристики связи между величинами X и Y рассматривается так называемый коэффициент корреляции
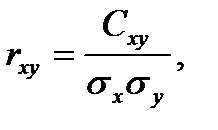 (6.5.35)
(6.5.35)
являющийся безразмерной величиной.
Если случайные величины X и Y независимы, то 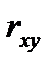 =0. Если же случайные величины X и Y связаны точной линейной зависимостью Y=aX+b, то
=0. Если же случайные величины X и Y связаны точной линейной зависимостью Y=aX+b, то 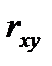 = sgna ,т.е.
= sgna ,т.е. 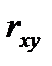 =1 при а > 0 и
=1 при а > 0 и 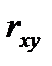 = -1 при а < 0. Вообще же коэффициент корреляции удовлетворяет условию
= -1 при а < 0. Вообще же коэффициент корреляции удовлетворяет условию
-1 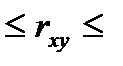 1.
1.
Задача 6.5.19
Дана таблица 6.5.1, определяющая закон распределения системы двух случайных величин (X,Y):
| X y | |||
3  |  | ||
2  | 4  | 2  | |
 | 2  | 5  |
Таблица 6.5.1
Найти: 1) коэффициент  ; 2) математическое ожидание
; 2) математическое ожидание 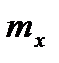 и
и 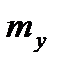 ;3) дисперсии
;3) дисперсии 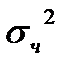 и
и 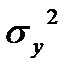 ; 4) коэффициент корреляции
; 4) коэффициент корреляции 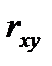 .
.
Решение.
Таблица 6.5.2
| X Y | ∑ | |||
3  |  | 4  | ||
2  | 4  | 2  | 8  | |
 | 2  | 5  | 8  | |
| ∑ | 6  | 7  | 7  | ∑20  =1 =1 |
| X y |  | |||
3  |  | 4  | ||
2  | 4  | 2  | 8  | |
 | 2  | 5  | 8  | |
 | 6  | 7  | 7  |  20 20  =1 =1 |
Таблица 6.5.3
  | -21 | -1 | |
| -12 | 3  |  | |
| -2 | 2  | 4  | 2  |
 | 2  | 5  |
Найдём  из условий (6.5.1):
из условий (6.5.1):
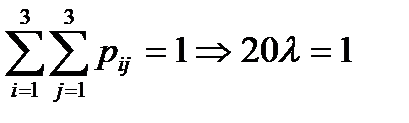
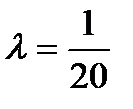
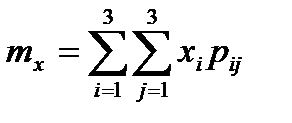
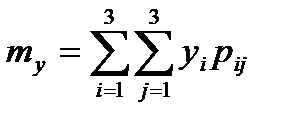
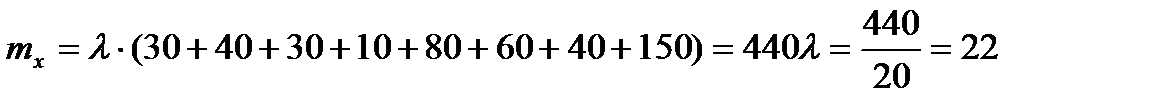
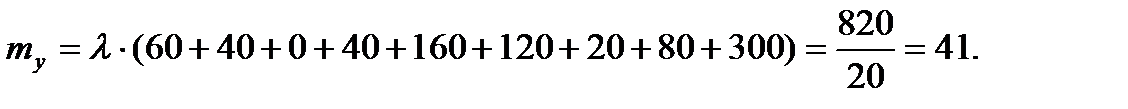
Вычислим дисперсии по формулам:
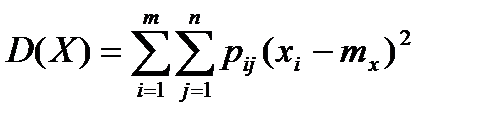 или
или 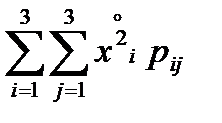 ,
,
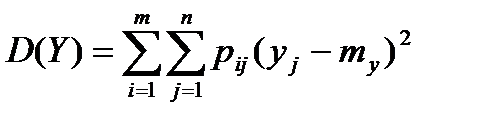 или
или 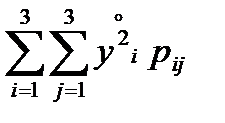 ,
,
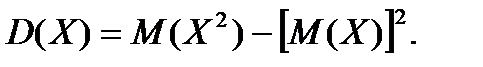
Вычислим 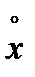 и
и 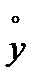 и составим таблицу 1.8.3
и составим таблицу 1.8.3
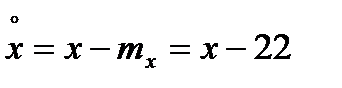
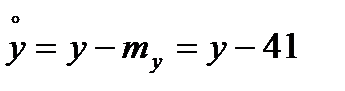
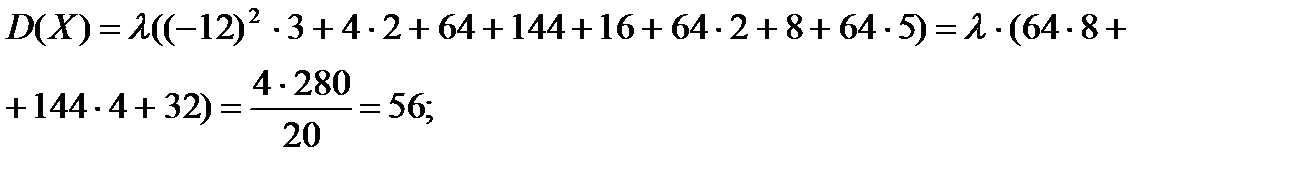
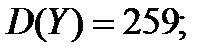
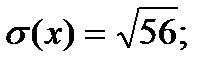
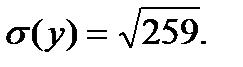
Определим ковариацию по формуле
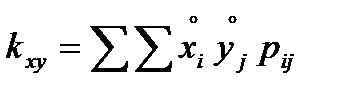
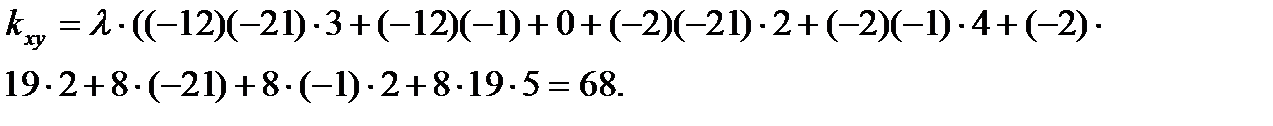
Вычислим коэффициент корреляции: 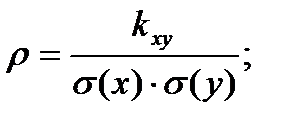
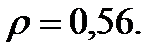
Математическая статистика
Вариационные ряды
Данная тема подробно изучается в курсе статистики. Однако ее основные вопросы будут неоднократно использоваться в дальнейшем. Поэтому их необходимо повторить перед ознакомлением с последующими темами. Кроме того, при изучении таких абстрактных понятий, как распределение дискретной случайной величины, математическое ожидание и дисперсия случайной величины, существенную помощь может оказать аналогия с распределением признака в виде вариационного ряда.
Основные формулы
Вариационный ряд (дискретный)
Таблица 6.6.1
| x1 | x1 | x2 | … | x1 | … | xm | Всего |
| n1 | n1 | n2 | … | n1 | … | nm | n |
Средняя арифметическая дисперсия:
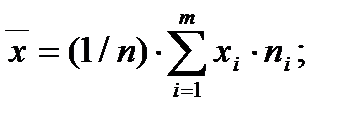
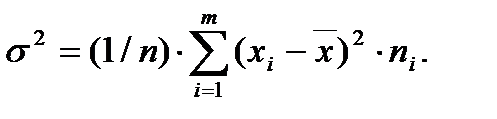
Формулы для упрощенных вычислений:
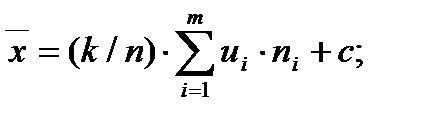
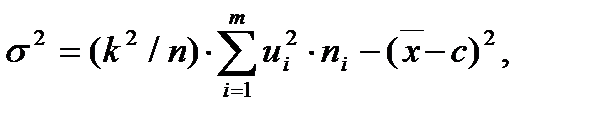
где 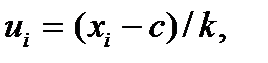 k и c –произвольные числа.
k и c –произвольные числа.
Выборочный метод. Общие вопросы.
Выборочный метод широко применяется на практике. Однако значение этой темы значительно шире, поскольку концепция выборки лежит в основе методологии математической статистики. Соотношение между характеристиками выборочной и генеральной совокупностей есть соотношение между опытными данными (результат наблюдений) и теоретической моделью. Основная идея выборки (выборочного наблюдения) заключается в следующем: определить неизвестные характеристики генеральной совокупности (генеральную), долю признака , генеральную среднюю 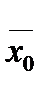 и генеральную дисперсию
и генеральную дисперсию 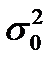 с помощью данных выборочного распределения.
с помощью данных выборочного распределения.
Рассматривается вероятность
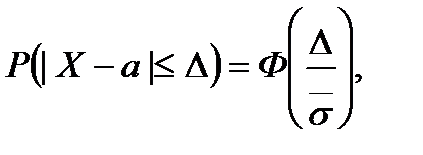
где X-выборочная доля () или выборочная средняя (xВ);
a-их математические ожидания (генеральная доля или генеральная средняя 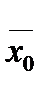 );
);
-предельная ошибка выборки;
P-доверительная вероятность;
X-, X+-доверительные границы;
средняя квадратическая ошибка.
