Раздел 11. Элементы математической статистики
1. Выборочный метод описания и анализа статистических данных.
2. Статистический вариационный ряд.
3. Интервальные статистические ряды.
4. Графическое представление статистических распределений выборки (полигон, гистограмма).
5. Эмпирическая функция распределения; её основные свойства.
6. Основные числовые характеристики выборки.
7. Начальные и центральные моменты k-го порядка, их использование в статистике.
8. Точечные оценки неизвестных параметров распределения.
9. Интервальные оценки параметров распределения.
10. Доверительная вероятность, доверительный интервал.
11. Статистическая гипотеза. Критерий согласия Пирсона.
13. Корреляционная зависимость.
14. Линейное уравнение регрессии; определение его параметров методом наименьших квадратов.
15. Выборочный коэффициент корреляции; его свойства. Коэффициент детерминации.
Перечень рекомендуемой литературы
Учебники
1. Белько И.В., Кузьмич К.К. Высшая математика для экономистов. Часть 1-3. – Мн.: Новое знание, 2006.
2. Белько И.В., Свирид Г.П. Теория вероятностей и математическая статистика. – Мн.: Новое знание, 2002.
3. Герасимович А.И., Рысюк Н.А. Математический анализ. Ч.1.-Мн.: Выш. школа, 1989.
4. Герасимович А.И., Кеда Н.П., Сугак М.Б. Математический анализ.Ч.2.-Мн.: Выш. школа, 1990.
5. Гурский Е.И. Основы линейной алгебры и аналитической геометрии. -Мн.: Выш. школа, 1982.
6. Красс М.С. Математика в экономике. – М.: ИД ФБК – ПРЕСС, 2005.
7. Мацкевич И.П., Свирид Г.П. Высшая математика. Теория вероятностей и математическая статистика. – Мн.: Выш. школа, 1993.
8. Пискунов Н.С. Дифференциальное и интегральное исчисление. В 2 ч. -М.: Наука, 1987. Ч.1.
9. Пискунов Н.С. Дифференциальное и интегральное исчисление. В 2 ч. -М.: Наука, 1987. Ч.2.
10. Письменный Д. Конспект лекций по высшей математике. 1часть.-М., Айрис Пресс,2004
11. Письменный Д. Конспект лекций по высшей математике. 2часть.-М., Айрис Пресс,2004
Задачники
12. Гурский Е.И. Руководство к решению задач по высшей математике. В 2ч. -Мн.: Выш. школа, 1989. Ч.1.
13. Гурский Е.И. Руководство к решению задач по высшей математике. В 2 ч. -Мн.: Выш. школа, 1990. Ч.2.
14. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. В 2 ч., ч.1. -М., Высш. школа, 1986, 1997, 1999
15. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. В 2 ч., Ч.2.-М., Высш. школа, 1986, 1997, 1999
16. Сухая Т.А., Бубнов В.Ф. Задачи по высшей математике. В 2 ч., ч.1-Мн.: Выш. школа, 1993.
17. Сухая Т.А., Бубнов В.Ф. Задачи по высшей математике. В 2 ч., ч.2.-Мн.: Выш. школа, 1993.
18. Индивидуальные задания по высшей математике (под ред. Рябушко А.П.). В 3 ч. -Мн.: Выш. школа, 2000.
19. Рябушко А.П. Индивидуальные задания по высшей математике. Мн.: Выш. школа, 2006
Контрольная работа №1
Задания 1-10. При условном делении экономики на три отрасли задана матрица коэффициентов прямых затрат А и вектор конечной продукции Y. Требуется:
1. Записать уравнение линейного межотраслевого баланса в координатной форме.
2. Найти плановые объемы выпуска валовой продукции отраслей. Систему линейных алгебраических уравнений решить методом Гаусса. Решение системы записать в неправильных дробях.
3. Выполнить проверку результата.
4. Записать приближенный ответ с точностью до сотых.
| 1. | А = 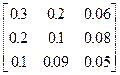 , Y = , Y = 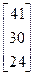 | 2. | А = 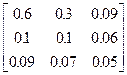 , Y = , Y = 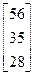 |
| 3. | А = 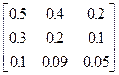 , Y = , Y = 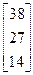 | 4. | А = 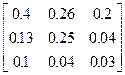 , Y = , Y = 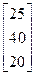 |
| 5. | А = 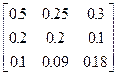 , Y = , Y = 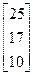 | 6. | А = 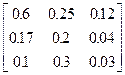 , Y = , Y = 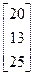 |
| 7. | А = 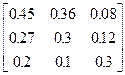 , Y = , Y = 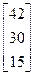 | 8. | А = 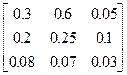 , Y = , Y = 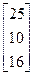 |
| 9. | А = 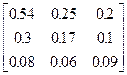 , Y = , Y = 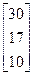 | 10. | А = 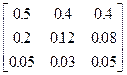 , Y = , Y = 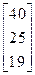 |
Задания 11-20.Даны векторы
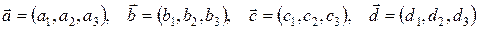 в некотором базисе.
в некотором базисе.
Показать, что векторы 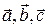 образуют базис и найти координаты вектора
образуют базис и найти координаты вектора 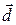 в этом базисе. Систему линейных уравнений решить по формулам Крамера.
в этом базисе. Систему линейных уравнений решить по формулам Крамера.
11. 
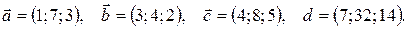
12. 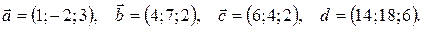
13. 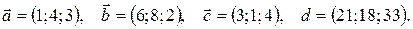
14. 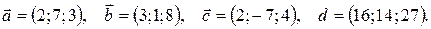
15. 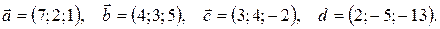
16. 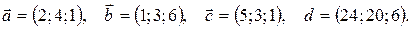
17. 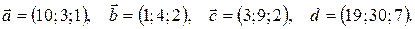
18. 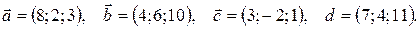
19. 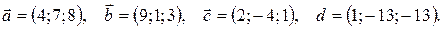
20. 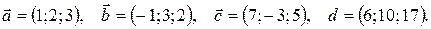
Задания 21-30. Даны координаты вершин пирамиды 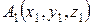 ,
, 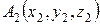 ,
, 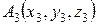 ,
, 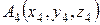 . Найти: 1) площадь грани
. Найти: 1) площадь грани 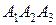 ;
;
2) объем пирамиды; 3) уравнения прямой 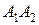 ; 4) уравнение плоскости
; 4) уравнение плоскости 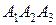 ; 5) уравнения высоты
; 5) уравнения высоты 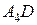 , опущенной из вершины
, опущенной из вершины 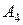 на грань
на грань 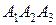 ; 6) длину высоты
; 6) длину высоты 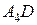 ; 7) координаты точки пересечения высоты
; 7) координаты точки пересечения высоты 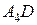 с плоскостью
с плоскостью 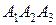 .
.
21. 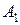 (3;1;4),
(3;1;4), 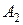 (-1;6;1),
(-1;6;1), 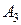 (-1;1;6),
(-1;1;6), 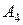 (0;4;-1).
(0;4;-1).
22. 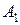 (3;-1;2),
(3;-1;2), 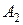 (-1;0;1),
(-1;0;1), 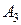 (1;7;3),
(1;7;3), 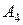 (8;5;8).
(8;5;8).
23. 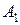 (3;5;4),
(3;5;4), 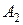 (5;8;3),
(5;8;3), 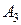 (1;2;-2),
(1;2;-2), 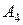 (-1;0;2).
(-1;0;2).
24. 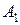 (2;4;3),
(2;4;3), 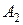 (1;1;5),
(1;1;5), 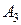 (4;9;3),
(4;9;3), 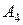 (3;6;7).
(3;6;7).
25. 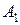 (9;5;5),
(9;5;5), 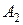 (-3;7;1),
(-3;7;1), 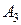 (5;7;8),
(5;7;8), 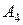 (6;9;2).
(6;9;2).
26. 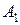 (0;7;1),
(0;7;1), 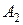 (2;-1;5),
(2;-1;5), 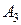 (1;6;3),
(1;6;3), 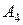 (3;-9;8).
(3;-9;8).
27. 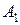 (5;5;4),
(5;5;4), 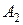 (1;-1;4),
(1;-1;4), 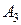 (3;5;1),
(3;5;1), 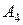 (5;8;-1).
(5;8;-1).
28. 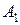 (6;1;1),
(6;1;1), 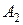 (4;6;6),
(4;6;6), 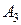 (4;2;0),
(4;2;0), 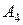 (1;2;6).
(1;2;6).
29. 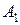 (7;5;3),
(7;5;3), 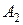 (9;4;4),
(9;4;4), 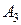 (4;5;7),
(4;5;7), 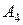 (7;9;6).
(7;9;6).
30. 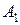 (6;8;2),
(6;8;2), 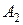 (5;4;7),
(5;4;7), 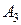 (2;4;7),
(2;4;7), 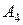 (7;3;7).
(7;3;7).
| 31. | На прямой 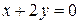 найти точку, равноудаленную от начала координат и от прямой найти точку, равноудаленную от начала координат и от прямой 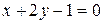 . Сделать чертеж. . Сделать чертеж. |
| 32. | Найти проекцию точки 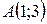 на прямую, проходящую через точку на прямую, проходящую через точку 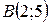 под углом 300 к оси Ох. Сделать чертеж. под углом 300 к оси Ох. Сделать чертеж. |
| 33. | Написать уравнение прямой, параллельной прямой 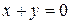 и отсекаю щей от координатных осей треугольник площадью 2 кв.ед. Сделать чертеж. и отсекаю щей от координатных осей треугольник площадью 2 кв.ед. Сделать чертеж. |
| 34. | Вычислить величину меньшего угла между прямыми 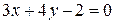 и и 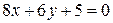 . Доказать, что точка . Доказать, что точка 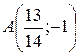 лежит на биссектрисе этого угла. Сделать чертеж. лежит на биссектрисе этого угла. Сделать чертеж. |
| 35. | Даны сторона прямоугольника 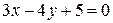 и две его вершины и две его вершины 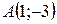 и и 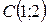 . Найти уравнения остальных сторон. Сделать чертеж. . Найти уравнения остальных сторон. Сделать чертеж. |
| 36. | Даны уравнение одной из сторон квадрата 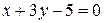 и точка и точка 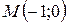 пересечения его диагоналей. Составить уравнения остальных трех сторон квадрата. Сделать чертеж. пересечения его диагоналей. Составить уравнения остальных трех сторон квадрата. Сделать чертеж. |
| 37. | Написать уравнение прямой, проходящей через точку пересечения прямых 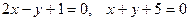 и пересекающей ось Ох под углом 300. Сделать чертеж. и пересекающей ось Ох под углом 300. Сделать чертеж. |
| 38. | Найти точку, симметричную точке 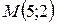 относительно прямой, проходящей через точки относительно прямой, проходящей через точки 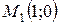 и и 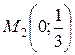 . Сделать чертеж. . Сделать чертеж. |
| 39. | Через начало координат проведена прямая на одинаковом расстоянии от точек 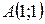 и и 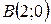 . Написать уравнение этой прямой. Сделать чертеж. . Написать уравнение этой прямой. Сделать чертеж. |
| 40. | Даны две вершины 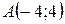 и и 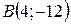 треугольника АВС и точка треугольника АВС и точка 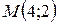 пересечения его высот. Найти вершину С. Сделать чертеж. пересечения его высот. Найти вершину С. Сделать чертеж. |
Задания 41-50.Вычислить пределы функций.
| 41. | |
1. 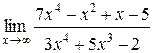 | 2. 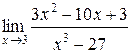 |
3. 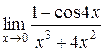 | 4. 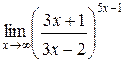 |
5. 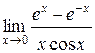 | |
| 42. | |
1. 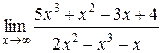 | 2. 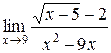 |
3. 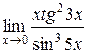 | 4. 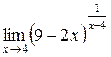 |
5. 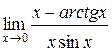 | |
| 43. | |
1. 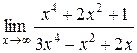 | 2. 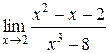 |
3. 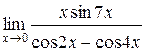 | 4. 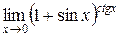 |
5. 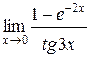 | |
| 44. | |
1. 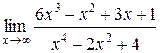 | 2. 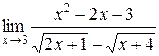 |
3. 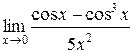 | 4. 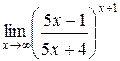 |
5. 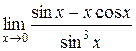 | |
| 45. | |
1. 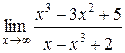 | 2. 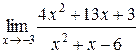 |
3. 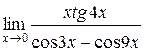 | 4. 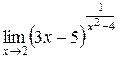 |
5. 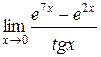 | |
| 46. | |
1. 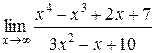 | 2. 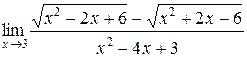 |
3. 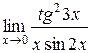 | 4. 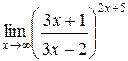 |
5. 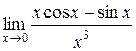 | |
| 47. | |
1. 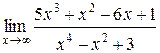 | 2. 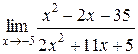 |
3. 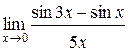 | 4. 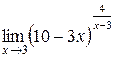 |
5. 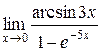 | |
| 48. | |
1. 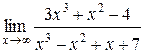 | 2. 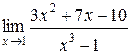 |
3. 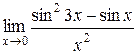 | 4. 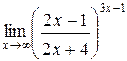 |
5. 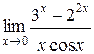 | |
| 49. | |
1. 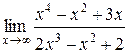 | 2. 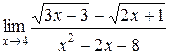 |
3. 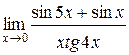 | 4. 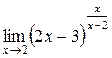 |
5. 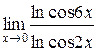 | |
| 50. | |
1. 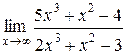 | 2. 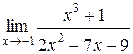 |
3. 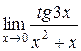 | 4. 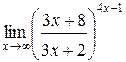 |
5. 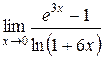 |
Задания 51-60. Найти производные 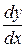 следующих функций.
следующих функций.
| 51. | ||
1. 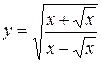 ; ; | 2. 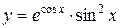 ; ; | 3. 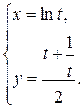 |
| 52. | ||
1. 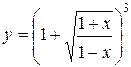 ; ; | 2. 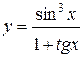 | 3. 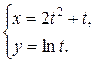 |
| 53. | ||
1. 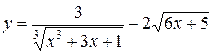 ; ; | 2. 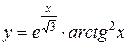 ; ; | 3. 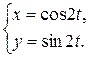 |
| 54. | ||
1. 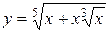 ; ; | 2. 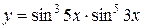 ; ; | 3. 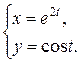 |
| 55. | ||
1. 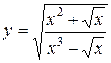 ; ; | 2. 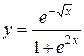 ; ; | 3. 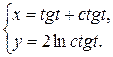 |
1. 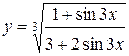 ; ; | 2. 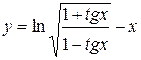 ; ; | 3. 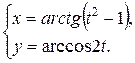 |
| 57. | ||
1. 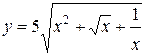 ; ; | 2. 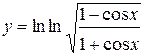 ; ; | 3. 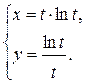 |
| 58. | ||
1. 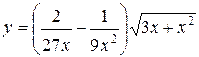 ; ; | 2. 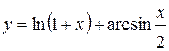 ; ; | 3. 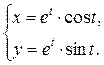 |
| 59. | ||
1. 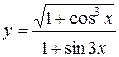 ; ; | 2. 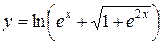 ; ; | 3. 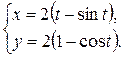 |
| 60. | ||
1. 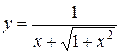 ; ; | 2. 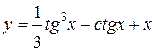 ; ; | 3. 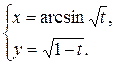 |
Задания 61-70. Исследовать методами дифференциального исчисления функцию 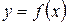 и, используя результаты исследования, построить ее график.
и, используя результаты исследования, построить ее график.
61. 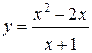 | 62. 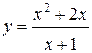 |
63. 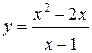 | 64. 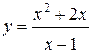 |
65. 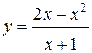 | 66. 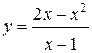 |
67. 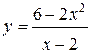 | 68. 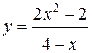 |
69. 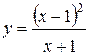 | 70. 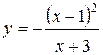 |
Контрольная работа № 2
Задания 71-80.Даны функция трех переменных 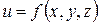 , точка
, точка 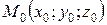 и вектор
и вектор 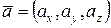 . Найти: 1) градиент функции
. Найти: 1) градиент функции 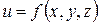 в точке
в точке 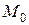 ; 2) производную функции
; 2) производную функции 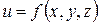 в точке
в точке 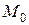 по направлению вектора
по направлению вектора 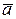 .
.
| 71. | 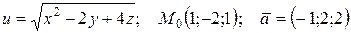 . . |
| 72. | 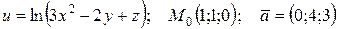 . . |
| 73. | 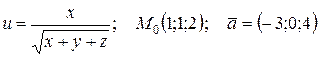 . . |
| 74. | 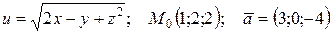 . . |
| 75. | 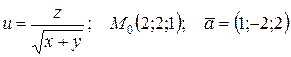 . . |
| 76. | 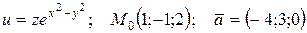 . . |
| 77. | 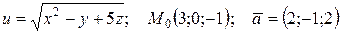 . . |
| 78. | 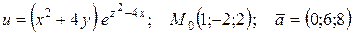 . . |
| 79. | 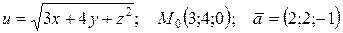 . . |
| 80. | 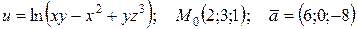 . . |
Задания 81-90.Производятся два вида товаров, объемы производства которых х и у, цены на эти товары 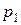 и
и 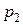 , соответственно, затраты на производство задаются функцией издержек
, соответственно, затраты на производство задаются функцией издержек 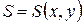 . Определить при каких объемах производства данных товаров прибыль будет максимальной; найти ее максимальное значение.
. Определить при каких объемах производства данных товаров прибыль будет максимальной; найти ее максимальное значение.
| № задания | 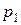 | 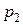 | 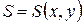 |
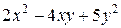 | |||
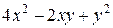 | |||
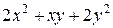 | |||
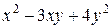 | |||
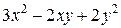 | |||
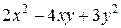 | |||
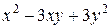 | |||
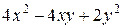 | |||
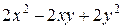 | |||
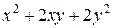 |
Задания 91-100.Найти неопределенные интегралы. В пунктах 1, 2 выполнить проверку дифференцированием.
| 91. | |
1. 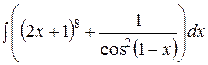 | 2. 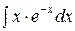 |
3. 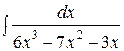 | 4. 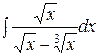 |
| 92. | |
1. 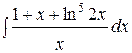 | 2. 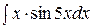 |
3. 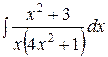 | 4. 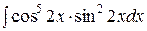 |
| 93. | |
1. 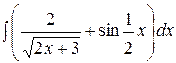 | 2. 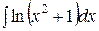 |
3. 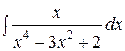 | 4. 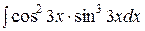 |
| 94. | |
1. 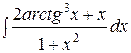 | 2. 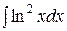 |
3. 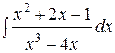 | 4. 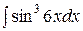 |
| 95. | |
1. 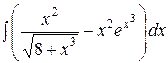 | 2. 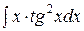 |
3. 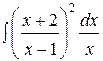 | 4. 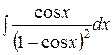 |
| 96. | |
1. 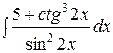 | 2. 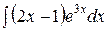 |
3. 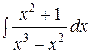 | 4. 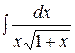 |
| 97. | |
1. 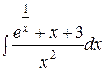 | 2. 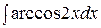 |
3. 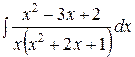 | 4. 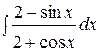 |
| 98. | |
1. 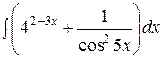 | 2. 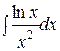 |
3. 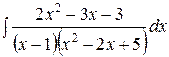 | 4. 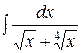 |
| 99. | |
1. 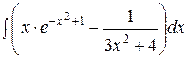 | 2. 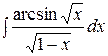 |
3. 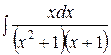 | 4. 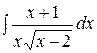 |
| 100. | |
1. 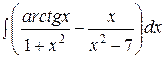 | 2. 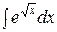 |
3. 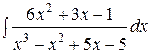 | 4. 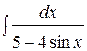 |
Задания 101-105.Сменная производительность труда рабочего описывается функцией 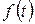 , где
, где 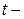 время в часах,
время в часах, 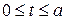 . Определить объем выпуска продукции в течение времени Т бригадой из n человек.
. Определить объем выпуска продукции в течение времени Т бригадой из n человек.
| Номер задания | Функция 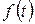 | a | T | n |
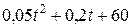 | ||||
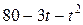 | ||||
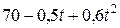 | ||||
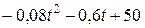 | ||||
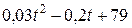 |
Задания 106-110.Известно, что спрос на некоторый товар описывается функцией 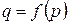 , а предложение данного товара характеризуется функцией
, а предложение данного товара характеризуется функцией 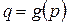 . Найти величину излишка потребителя при покупке данного товара.
. Найти величину излишка потребителя при покупке данного товара.
| Номер задания | 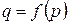 | 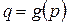 |
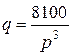 | 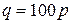 | |
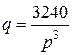 | 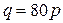 | |
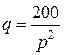 | 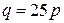 | |
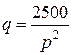 | 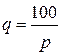 | |
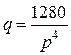 | 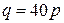 |
Задания 111-120. Найти частное решение дифференциального уравнения первого порядка, удовлетворяющее условию 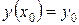 .
.
111. 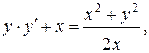 | 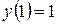 . . |
112. 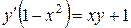 , , | 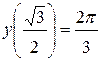 . . |
113. 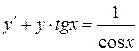 , , | 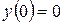 . . |
114. 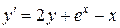 , , | 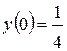 . . |
115. 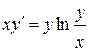 , , | 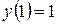 . . |
116. 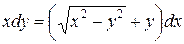 , , | 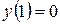 . . |
117. 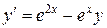 , , | 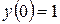 . . |
118. 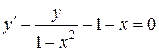 , , | 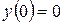 . . |
119. 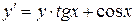 , , | 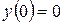 . . |
120. 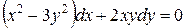 , , | 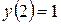 . . |
Задания 121-130. Найти общее решение дифференциального уравнения.
121. 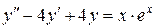 . . | 122. | 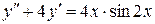 . . |
123. 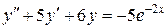 . . | 124. | 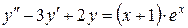 . . |
125. 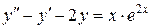 . . | 126. | 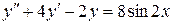 . . |
127. 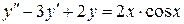 . . | 128. | 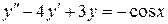 . . |
129. 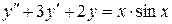 . . | 130. | 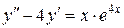 . . |
Контрольная работа № 3
Задания 131-140. Исследовать числовой ряд на сходимость.
131. 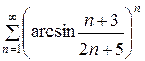 . . | 132. 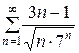 . . |
133. 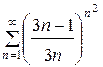 . . | 134. 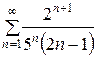 . . |
135. 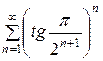 . . | 136. 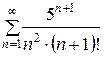 . . |
137. 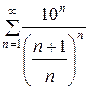 . . | 138. 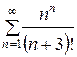 . . |
139. 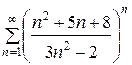 . . | 140. 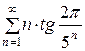 . . |
Задания 141-150.Найти область сходимости степенного ряда.
141. 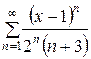 . . | 142. 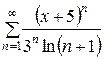 . . |
143. 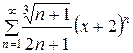 . . | 144. 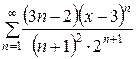 . . |
145. 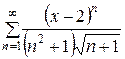 . . | 146. 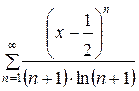 . . |
147. 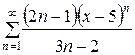 . . | 148. 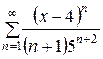 . . |
149. 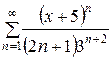 . . | 150. 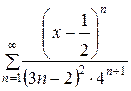 . . |
151. В течение года три фирмы могут обанкротиться независимо друг от друга с вероятностями 0,2; 0,3; 0,5. Найти вероятность того, что в конце года 1)обанкротятся ровно две фирмы; 2) хотя бы одна фирма.
152. Вероятность аудиторской проверки в течение года для Беларусбанка равна 0,8, а для Приорбанка – 0,9. Найти вероятность того, что в течение года будут проверены 1) оба банка; 2) хотя бы один банк.
153. Вероятность того, что потребитель увидит рекламу по каждому из трех телеканалов соответственно равна 0,4; 0,6; 0,7. Какова вероятность того, что потребитель увидит рекламу 1) только по одному из каналов; 2) по всем трем каналам.
154. Вероятность получения заказа в текущем году для первой строительной фирмы равна 0,95, для второй – 0,8, для третьей – 0,5. Найти вероятность того, что в текущем году 1) ни одна фирма не получит заказа; 2) две фирмы получат заказ.
155. Надежность первой компании в течение времени t оценивается на уровне 95%, второй – 70%, третьей – 80%. Найти вероятность того, что в течение времени t 1) все три компании не станут банкротами; 2) хотя бы две компании станут банкротами.
156. Вероятность того, что в течение недели покупатель посетит гипермаркет А, равна 0,85, а гипермаркет В – 0,9. Какова вероятность того, что в течение недели: 1) покупатель посетит оба магазина; 2) только один из них.
157. Экзаменационный билет содержит три вопроса. Вероятность того, что студент ответит на первый, второй и третий вопрос, соответственно, равна 0,92; 0,8 и 0,75. Найти вероятность того, что студент сдаст экзамен, если для этого необходимо ответить 1) на все вопросы; 2) по крайней мере на два вопроса.
158. Вероятности того, что сальдо внешней торговли будет положительным для трех стран соответственно равны 0,74; 0,83 и 0,9. Найти вероятности событий: 1) только две страны будут иметь положительное сальдо; 2) все страны будут иметь отрицательное сальдо.
159. Строительная отрасль выпускает акции трех видов А, В и С. Вероятности того, что акции через месяц поднимутся в цене соответственно равны 0,85; 0,9; 0,93. Какова вероятность того, что через месяц поднимутся в цене 1) акции только одного вида; 2) акции всех видов.
160. Предприятие состоит из трех независимо работающих подразделений. Предполагается, что вероятность их рентабельной работы за два месяца соответственно равна 0,65; 0,7; 0,82. Найти вероятность того, что в течение двух месяцев рентабельным будет 1) хотя бы одно из подразделений; 2) ровно два подразделения.
161. В бухгалтерии банка имеются два списка должников. В первом – фамилии 10 мужчин и 12 женщин, во втором – 8 мужчин и 4 женщин. Одна фамилия случайно переносится из первого списка во второй. Затем фамилия одного из должников случайно выбирается из второго списка. Найти вероятность того, что это будет фамилия мужчины.
162. Вероятность того, что новый товар будет пользоваться спросом на рынке, если конкурент не выпустит аналогичный, равна 0,91, а при наличии конкурирующего – 0,32. Вероятность выпуска конкурентом товара равна 0,45. Найти вероятность того, что товар будет пользоваться спросом на рынке.
163. Лизинговая компания предоставляет в аренду на определенных условиях дорогостоящее оборудование с вероятностью 0,9, если экономическая ситуация в стране не будет ухудшаться в течение времени t. Если же экономическая ситуация будет ухудшаться, то эта вероятность равна 0,65. Экономист-консультант полагает, что в течение времени t с вероятностью 0,72 ситуация в стране будет становиться хуже. Чему равна вероятность того, что лизинговая компания предоставит оборудование в аренду?
164. Отдел маркетинга полагает, что в ближайшее время ожидается рост спроса на услуги данной строительной фирмы с вероятностью 0,7. Фирма, занимающаяся прогнозом рыночной ситуации, подтверждает предположение о росте спроса. Положительный прогноз фирмы сбывается на 90%, а отрицательный – на 80%. Найти вероятность того, что рост спроса действительно произойдет.
165. Три фирмы поставляют товар в данный регион в соотношении 2:3:5. Среди продукции первой фирмы высококачественные изделия составляют 85%, у второй – 90%, у третьей – 80%. Взятый наугад товар оказался отличного качества. Найти вероятность того, что он изготовлен третьей фирмой.
166. Курс евро повышается в течение полугода с вероятностью 0,7, остается неизменным с вероятностью 0,2 и понижается с вероятностью 0,1. При повышении курса предприятие надеется получить прибыль с вероятностью 0,2, при неизменном курсе – с вероятностью 0,5, при понижении курса – с вероятностью 0,8. Найти вероятность того, что предприятие получит прибыль.
167. На заводе строительного оборудования первый цех выпускает 25% всех изделий, второй – 45%, третий – 30% . В их продукции брак составляет соответственно 3%, 2%, 4%. Какова вероятность того, что случайно выбранное изделие является дефектным?
168. У студента S есть три любимых места для прогулок, которые он посещает с одинаковой вероятностью. Вероятность того, что он встретит своего друга в первом месте, равна  , во втором
, во втором 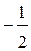 , в третьем
, в третьем 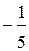 . Известно, что встреча произошла. Какова вероятность того, что студент S выбрал первое место?
. Известно, что встреча произошла. Какова вероятность того, что студент S выбрал первое место?
169. Вероятность того, что коэффициент Джини G, который показывает равномерность распределения доходов среди населения страны, будет находиться в области 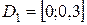 равна 0,07, в области
равна 0,07, в области 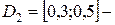 0,8, в области
0,8, в области 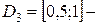 0,13. Вероятности социальной нестабильности общества для коэффициента G из областей
0,13. Вероятности социальной нестабильности общества для коэффициента G из областей 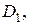
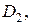
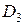 соответственно равны 0,015; 0,08; 0,6. Найти вероятность того, что данная страна социально стабильна.
соответственно равны 0,015; 0,08; 0,6. Найти вероятность того, что данная страна социально стабильна.
170. Имеются две неотличимые по внешнему виду игральные кости: обычная и фальшивая, при случайном подбросе которой «шестерка» выпадает с вероятностью 1/3, «единица» - с вероятностью 1/9, а остальные цифры выпадают с одинаковой вероятностью. Подброшена наудачу выбранная кость и в результате выпала «четверка». Найти вероятность того, что была подброшена обычная игральная кость.
Задания 171-180.Непрерывная случайная величина (СВ) Х задана функцией распределения 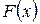 . Найти:
. Найти:
1) коэффициент А;
2) плотность распределения вероятностей 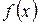 ;
;
3) математическое ожидание СВ Х;
4) вероятность события 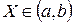 .
.
| 171. | 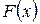 = = 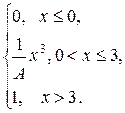 |  . . |
| 172. | 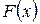 = = 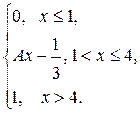 | 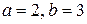 . . |
| 173. | 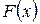 = = 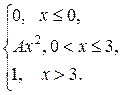 | 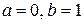 . . |
| 174. | 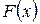 = = 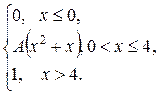 | 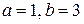 . . |
| 175. | 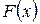 = = 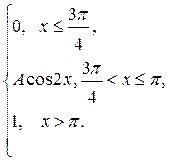 | 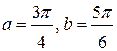 . . |
| 176. | 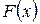 = = 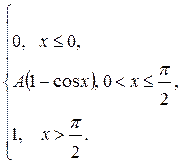 | 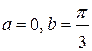 . . |
| 177. | 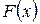 = = 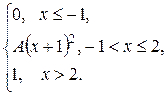 | 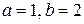 . . |
| 178. | 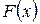 = = 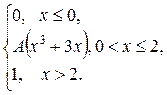 | 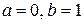 . . |
| 179. | 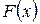 = = 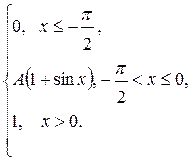 | 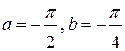 . . |
| 180. | 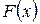 = = 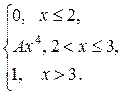 | 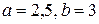 . . |
Задания 181-190.
Зависимость выпуска валовой продукции (СВ Y) от стоимости основных фондов (СВ Х) 50 предприятий представлена корреляционной таблицей.
Требуется:
1. Найти уравнение прямой линии регрессии Y на Х.
2. Найти уравнение прямой линии регрессии Х на Y.
3. Построить графики полученных прямых.
4. Оценить тесноту корреляционной связи, используя выборочный коэффициент корреляции.
| 181. | Х Y | 0,8 | 2,4 | 4,0 | 5,6 | 7,2 | mi |
| 0,7 | |||||||
| 2,1 | |||||||
| 3,5 | |||||||
| 4,9 | |||||||
| 6,3 | |||||||
| mj |
| 182. | Х Y | 0,7 | 2,1 | 3,5 | 4,9 | 6,3 | mi |
| 0,4 | |||||||
| 1,2 | |||||||
| 2,0 | |||||||
| 2,8 | |||||||
| 3,6 | |||||||
| mj |
| 183. | Х Y | 0,8 | 2,0 | 3,2 | 4,4 | 5,6 | mi |
| 0.6 | |||||||
| 1,4 | |||||||
| 2,2 | |||||||
| 3,0 | |||||||
| 3,8 | |||||||
| mj |
| 184. | Х Y | 1,2 | 2,4 | 3,6 | 4,8 | 6,0 | mi |
| 1,8 | |||||||
| 3,6 | |||||||
| 5,4 | |||||||
| 7,2 | |||||||
| 8,0 | |||||||
| mj |
