Дерева і ліс

Особливий інтерес представляють зв'язкові ацикличні графи, називані деревами. Дерево на безлічі 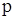вершин завжди містить 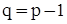ребер, тобто мінімальну кількість ребер, необхідну для того, щоб граф був зв’язним. Дійсно, дві вершини зв'язуються одним ребром, і для зв'язку кожної наступної вершини з попередніми потрібно ребро, отже, для зв'язку 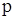вершин необхідно і достатньо 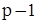ребер.

При додаванні в дерево ребра утвориться цикл, а при видаленні хоча б одного ребра дерево розпадається на компоненти, кожна з який являє собою також дерево або ізольовану вершину. Незв'язний граф, компоненти якого є деревами, називається лісом (ліс із 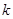дерев, що містить 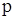вершин, має в точності 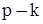ребер). Сказане ілюструється на прикладі дерева (мал. 3.9,а), що перетворюється в циклічний граф додаванням ребра (мал. 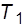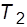3.9,б) і розпадається на ліс із двох дерев і при видаленні ребра (мал. 3.9, в).

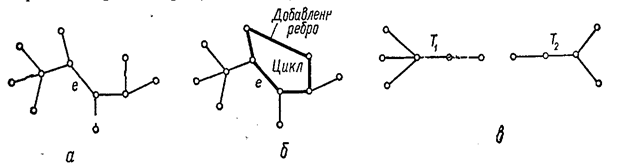
Мал. 3.9. Дерево (а), утворення циклу при введенні додаткового ребра (б) і ліс, що утвориться після видалення ребра 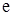(в).

Звичайно дерева вважаються істотно різними, якщо вони не ізоморфні. На мал. 3.10 показані всі можливі різні дерева із шістьма вершинами. Зі збільшенням числа вершин кількість різних дерев різко зростає (наприклад, при 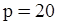їх нараховується біля мільйона). Серед різних дерев виділяються два важливі окремі випадки: послідовне дерево, що представляє собою простий ланцюг, і зоряне дерево, у якому одна з вершин (центр) суміжна з всіма іншими вершинами.

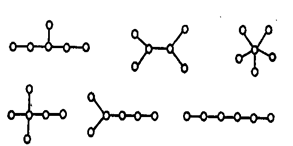
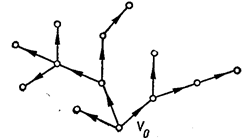
Мал. 3.10. Істотно різні дерева із шістьма вершинами.

Мал. 11. Прадерево з коренем .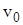

Розглядаються також дерева з орієнтованими ребрами (дугами). Орієнтоване дерево називається прадеревом із коренем 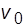, якщо існує шлях між вершиною 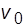і будь-якою іншою його вершиною (мал. 3.11). Ясно, що прадерево має єдиний корінь.

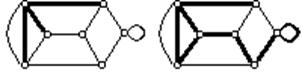
Дотепер розглядалися дерева як мінімальні зв’язні графи на безлічі 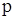вершин. Важливе значення має й інша точка зору, коли дерева або ліс є частинами деякого графа, тобто утворюються з його ребер. Будь-яка зв'язкова сукупність ребер, що не містить контурів, разом із інцидентними їм вершинами утворює дерево графа (мал. 3.12,а). Якщо таке дерево є суграфом (містить усі вершини графа), то воно називається покриваючим деревом, або кістяком (мал. 3.12,б). Так як петля являє собою найпростіший цикл, що перебуває з єдиного ребра, то вона не може входити до складу будь-якого дерева графа. Ребра графа, що належать його дереву, називають гілками. Якщо дерево покриває граф, то множина ребер графа розбивається на дві підмножини: підмножина гілок і підмножина ребер доповнення дерева, називаних хордами. При цьому зв'язковий 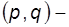граф містить 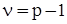гілок і 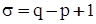хорд. Якщо граф незв'язний, то сукупність кістяків 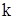його компонент утворить покриваючий ліс. У цьому випадку 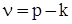і .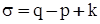

а б

Мал. 3.12. Дерево як частина графа (виділено жирними лініями):

а — дерево; б — кістяк ( дерево , що покриває ,).

Дерева грають важливу роль у різних прикладних завданнях, коли, наприклад, мова йде про зв'язок яких-небудь об'єктів мінімальним числом каналів (ліній зв'язку, доріг, комунікацій) із визначеними властивостями. За допомогою дерева визначається система координат при моделюванні ланцюгів і систем різної фізичної природи. Дерева використовуються в якості моделей при розгляді ієрархічних систем об'єктів, структурних формул органічних сполук і т.п.

ПЛАНАРНОСТЬ

Граф називають плоским (планарным), якщо існує ізоморфний йому граф (геометрична реалізація), що може бути зображений на площині без перетинання ребер. Наприклад, хоча в одному з графів на мал. 10 ребра перетинаються, ізоморфні йому не мають перетинань, отже, він плоский.

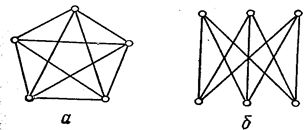
Мал. 3.13. Графи Понтрягина — Куратовского:

а — повний п'ятикутник; б — двочастковий граф.

На мал. 3.13 показані два неплоских графи, що грають фундаментальну роль у теорії планарности і називані графами Понтрягіна - Куратовського. Повний п'ятикутник (мал. 3.13,а) являє собою простий неплоский граф із мінімальним числом вершин (повний граф із чотирма вершинами — плоский, а видалення з п'ятикутника хоча б одного ребра також перетворює його в плоский граф). Двочастковий граф (мал. 3.13,б) є моделлю відомого завдання про три будинки і три колодязя: чи можна прокласти від будинків до кожного колодязя дороги так, щоб вони не перетиналися (ворогуючі сусіди повинні мати можливість користуватися всіма колодязями, але не хочуть зустрічатися на дорогах)?

Властивості планарности не порушуються, якщо деяке ребро розбити на два введенням нової вершини другого ступеня або замінити два ребра, які інцидентні вершині другого ступеня, одним ребром, видалив цю вершину. Два графи називають гомеоморфними (ізоморфними з точністю до вершин другого ступеня), якщо після видалення з них вершин другого ступеня й об'єднання інцидентних цим вершинам ребер, вони виявляються ізоморфними (мал. 3.14). Очевидно, граф, гомеоморфний плоскому графу, також плоский.

Строго доводиться, що граф є плоским тоді і тільки тоді, коли він не містить підграф, гомеоморфний одному з графів Понтрягина—Куратовского.

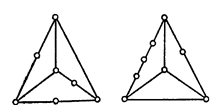
Мал. 3.14. Гомеоморфні графи.

Планарність є істотною властивістю графів, що моделюють комунікації і зв'язкі між об'єктами на площині (дороги між населеними пунктами, водопровідні і газопровідні мережі, лінії передач електроенергії…). Плоскими графами представляються різні карти, із якими, зокрема, зв'язана відома проблема чотирьох фарб: чи завжди можна розфарбувати області, на які плоский граф поділяє поверхню, так, щоб ніякі дві суміжні області не були пофарбовані в однаковий колір і щоб при цьому було використано не більш чотирьох кольорів? Доведено, що для такого розфарбування в будь-якому випадку досить п'ятьох фарб, але ніхто ще не привів приклада, коли п'ять фарб дійсно необхідні. Проблема залишається невирішеної, незважаючи на величезні зусилля багатьох видатних математиків, що штурмують її більш сторіччя.