Гіпотеза про однорідність вибірки

Перевірка вибірки на однорідність – перший етап математичної обробки результатів спостережень. Задача зводиться до перевірки гіпотези 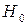: вибірка однорідна, при 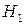: вибірка обтяжена промахами.

Дані експерименту розставляють в порядку зростання: 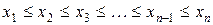. На промах перевіряються крайні ліві або крайні праві значення даного ряду.

При різних об’ємах вибірки для аналізу на промах величини 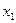використовують статистики 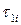, , 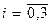а для 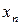відповідно статистики 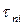, , 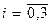які обчислюються за формулами:

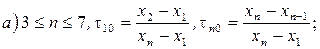
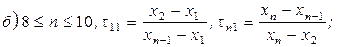
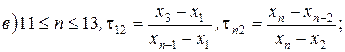
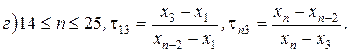
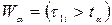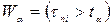Критична область , або , де 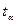знаходять з таблиці 11 у додатку.

Приклад 4.7. При експертній оцінці вагомості фактору „Характер бізнесу клієнта”, який впливає на внутрішньогосподарський ризик, групою з 20 експертів отримано наступні результати:

8,5,20,8,5,18,8,5,10,8,15,8,5,10,35,5,10,5,10,12.

Перевірити вибірку на однорідність для рівня значущості .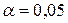

Розв’язок. Запишемо одержані результати в порядку зростання:

5,5,5,5,5,5,8,8,8,8,8,10,10,10,10,12,15,18,20,35.

Крайню справа величину 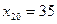перевіряємо на промах. Знаходимо:

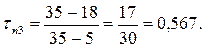
За таблицею 10 у додатку знаходимо 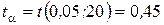. Оскільки 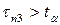, то значення 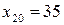вважаємо промахом.

Розв’язок даної задачі дає можливість керівнику експертної групи зробити висновок про оцінювання вагомості даного фактору кожним експертом. Зокрема експертом, який дав оцінку .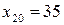

У випадку 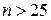розраховують 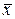і 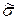. Якщо значення 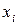попадає в проміжок 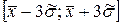, то воно не вважається промахом. В іншому випадку його вважають промахом.

Критерій знаків

Нехай 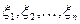і 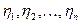- n пар випадкових величин, для яких різниці 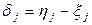можна подати у вигляді 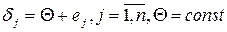, а випадкові величини 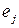: 1) незалежні; 2) неперервно розподілені; 3) симетрично розподілені відносно нуля (симетричність розподілів 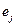означає, що розподіли 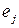та - 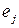збігаються).

Зауважимо, що розподіли випадкових величин 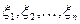та 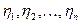неперервні, але невідомі (і вони можуть бути, взагалі кажучи, різними як і розподіли випадкових величин ).

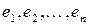Щодо невідомого параметра 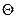висувається гіпотеза 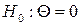. Альтернативними до неї є ; ; .

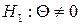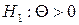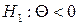Справджується чи ні гіпотеза 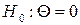, випадкові величини 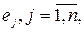неперервно й симетрично розподілені відносно нуля і незалежні. Звідси випливає, що випадкова величина, яка дорівнює кількості випадкових величин 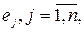що набули додатних значень має біноміальний розподіл із параметрами 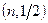і тому кількість даних величин серед 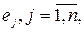, близька до половини наявних, тобто до .

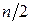Позначимо через 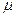кількість додатних різниць серед 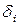. Тоді при перевірці гіпотези 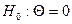її природно відхиляти, якщо кількість додатних різниць 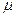істотно відрізняється від 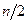і не відхиляти в іншому випадку.

Критична точка 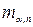визначається як мінімальне число m , для якого 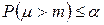, де 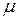- біноміально розподілена випадкова величина з параметрами n та 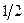. Для заданого рівня значущості 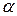значення 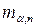знаходять за таблицею 12 у додатку.

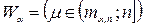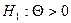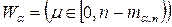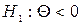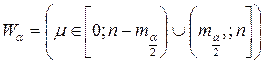Критична область при ; при ; при .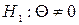

Якщо зняти вимогу про неперервність розподілів випадкових величин 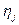і 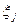, то різниці 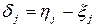, 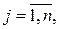можуть набувати нульових значень з ненульовою ймовірністю. В даному випадку критерій знаків можна застосувати до відмінних від нуля різниць, відкинувши нульові.

Приклад 4.8 Групою з 20 експертів проводилася оцінка вагомості факторів „Характер бізнесу клієнта” і „Професійність і чесність адміністрації” та отримано наступні результати:

8, 5, 20, 8, 5, 18, 8, 5, 10, 8, 15, 8, 5, 10, 35, 5, 10, 5, 10, 12.

4, 5, 20, 5, 3, 6, 10,15,10, 9, 8, 40, 8, 5, 10, 20, 18, 20, 10, 20.

Для рівня значущості 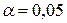перевірити нульову гіпотезу 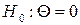про співпадання оцінок експертів при альтернативній гіпотезі 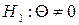про їх відмінність.

Розв’язок. Позначимо через 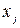- оцінки першого фактору, 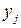– другого, а 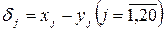. Тоді різниці 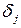будуть мати наступні знаки:

+, 0, 0, +, +, +, -, -, 0, -, +, -, -, +, +, -, -, -, 0, -.

Кількість різниць відмінних від нуля 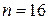, а кількість додатних різниць 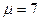. Тоді з таблиці 12 у додатку для 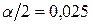і 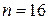знаходимо, що область прийняття гіпотези 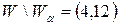. Таким чином гіпотеза 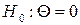приймається, тобто нема істотної різниці в оцінках експертів.

Часто при перевірці гіпотези 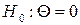користуються критерієм Фішера. Зокрема, при альтернативній гіпотезі 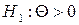статистика 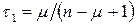, число ступенів свободи 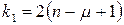, , 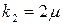критична область .

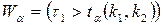При альтернативній гіпотезі , , , , .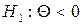

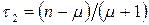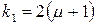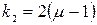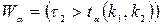При альтернативній гіпотезі 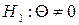гіпотеза 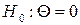відхиляється, якщо виконується одна з нерівностей: 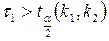або .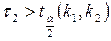

Зокрема для прикладу 4.8 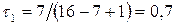, , 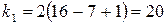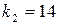. За таблицею 8 у додатку 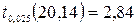. Оскільки, 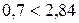, то гіпотеза 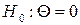приймається.

Критерій серій

Даний критерій застосовується для перевірки гіпотези 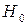, в якій стверджується, що елементи вибірки одержані випадковим чином і незалежні. Нехай 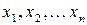– вибірка результатів спостережень, а 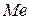медіана, обчислена на основі результатів спостережень. Кожному елементу вибірки ставиться у відповідність знак „+” або „-” в залежності від того, чи його значення більше або менше за медіану (нульові значення різниць не враховуються). Таким чином, всій вибірці поставлено у відповідність певний набір знаків. Позначимо через 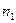число знаків „+”, а 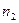– число знаків „-” в одержаному наборі. Серією в цьому наборі називається будь – яка послідовність, яка складається з однакових знаків і обмежена протилежними знаками, або знаходиться на початку чи в кінці набору.

Наприклад, в наборі: +,-,+,+,+,-,-,-,-,-,+,+ міститься 5 серій, а , .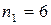

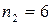Статистикою критерію серій є число серій N. Критична область 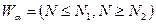. Значення 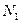і 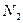задаються таблицею 13 у додатку.

При великих об’ємах вибірки, коли аб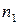о , або 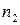, або обидва значення 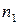і 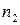більші 20 для перевірки гіпотези 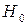можна використати статистику 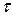, точкова оцінка якої 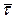обчислюється за формулою

.

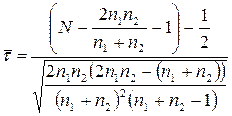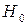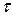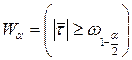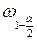При умові, що вірна гіпотеза , статистика має приблизно нормальний розподіл N(0,1). В цьому випадку критична область , де знаходять за таблицею 2а у додатку.

Приклад 4.9 Розподіл середньомісячної зарплати в 1999р. по регіонах України представляється у вигляді ряду:168, 129, 118, 209, 220, 134, 130, 215, 140, 191, 137, 184, 152, 169, 183, 173, 135, 150, 112, 184, 143, 127, 146, 123, 141, 303, 187. Чи можна для рівня значущості 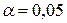вважати отримані результати випадковими?

Розв’язок. Знайдемо оцінку медіани отриманих результатів. Для цього представимо їх у виді рангованого ряду:

112,118,123,127,129,130,134,135,137,140,141,143,146,150,152,168,169,173,183,184,187,191,209,215,202,303.

Для нього Me=150, а відповідна послідовність знаків:

+, -, -, +, +, -, -, +, -, +, -, +, +, +, +, +, -, -, +, -, -, -, -, -, +, +, де 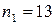, , 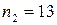число серій N=13. За таблицею 13 додатку при 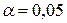знаходимо 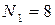, 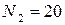.Таким чином, гіпотеза 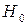приймається. Отримані результати можна вважати випадковими.

4.4.5. Перевірка гіпотези про однорідність двох вибірок. Критерій Вілкоксона

Нехай 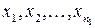і 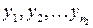– дві незалежні вибірки. Перевірка гіпотези про однорідність двох вибірок в припущенні, що 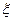і 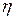– неперервні випадкові величини, зводиться до перевірки нульової гіпотези 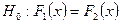, яка полягає в тому, що при всіх значеннях x функції розподілу обох вибірок рівні між собою.

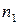
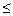
Припустимо, що 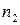(в протилежному випадку вибірки можна поміняти місцями).

Для даного рівня значущості 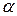перевірку нульової гіпотези 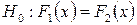проводять за схемою:

1. Записують варіанти обох вибірок в зростаючому порядку у виді ряду і знаходять в ньому величину 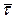- суму порядкових номерів варіант першої вибірки в цьому ряді.

2. Критична область 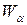визначається альтернативною гіпотезою .

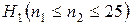а) 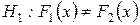, 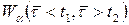. З таблиці критичних точок розподілу Вілкоксона (таблиця 14 у додатку) знаходять , .

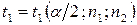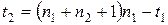б) 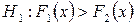, , 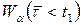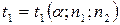знаходять з таблиці 14 у додатку.

в) , , .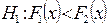

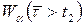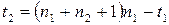Зауваження 4.7. Якщо декілька варіантів однієї вибірки однакові, то в спільному ряді їх нумерують послідовно ніби вони є різними числами.

Зауваження 4.8. Якщо співпадають варіанти різних вибірок, то їм усім присвоюють порядковий номер, який дорівнює середньому арифметичному тих номерів, які б мали ці варіанти якби були різними.

Приклад. 4.10. При експертній оцінці вагомості факторів, що впливають на внутрішньогосподарський ризик двома експертами отримано наступні результати

І 1 8 15 10 8 9 11 9 8 4 2 6 5 5.

ІІ 11 15 16 10 3 5 13 8 3 7 8 2 1 9.

Для рівня значущості 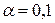перевірити нульову гіпотезу 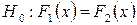про однорідність оцінок обох експертів при альтернативній гіпотезі .

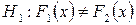Розв’язок. Розмістимо отримані результати в порядку зростання:

1,2,2,3,3,4,5,5,5,6,7,8,8,8,8,8,9,9,9,10,10,11,13,15,15,16.

Пронумеруємо елементи цього ряду, враховуючи зауваження 4.7. і 4.8.

2,5

2,5

					20,5	20,5			24,5	24,5

Обчислимо суму рангів першої вибірки

.

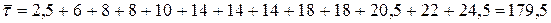Оскільки альтернативна гіпотеза 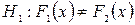, то критична область двостороння. Для рівня значущості 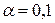і чисел ступенів свободи 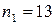і 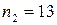за таблицею 13 у додатку знаходимо 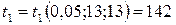. Тоді .

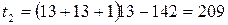З того що 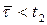, випливає, що нульова гіпотеза приймається, тобто нема суттєвої розбіжності в оцінюванні обох експертів.

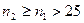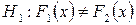Якщо і , то 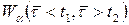, , 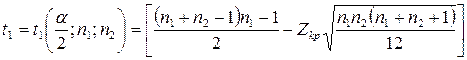(4.15)

де 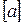- ціла частина числа 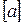, 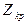– розв’язок рівняння , .

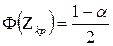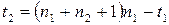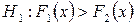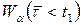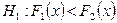Якщо , то ; , то ,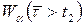

де 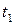визначається за формулою (4.15) в якій 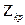є розв’язком рівняння .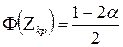