Граф. топологиялық матрицалар

Электр тізбегінің барлық тармақтарын жай сызықпен белгілеп, шын токтардың бағыты белгіленген күйдегі схеманың сұлбасы граф деп аталады.

Жай сызықпен белгіленген схеманың тармақтары граф тармақтары деп аталады. Әрбір екі тармақтың шекарасындағы нүкте граф түйіні деп аталады. Әр тармақтың өз бағыты болады. Подграф дегеніміз графтың бір тармағы немесе графтың кез келген бір түйіні.

Топологиялық матрицала

Бейнені анықтаудың нақты программасы болмағандықтан тізбектің топологиясының суретін есептеуіш машинаға беру қиындық туғызады. Сондықтан тізбек топологиясын ЭЕМ–ге топологиялық матрица деп аталатын матрица түрінде енгізеді. Мұндай матрицаларды 3 түрге бөледі: түйіндік матрица, контурлы матрица, қисындық матрица.

Түйіндік матрица – Кирхгофтың бірінші заңына құрылған теңдеулер коэффиценттерінің таблицасы. Матрицаның i жолы m түйіннің санымен, j бағаны n тармақтың санымен сипатталады. a_ij – элементтері, i-жол саны, j-баған саны.I=1 : (m-1); j=1 : n.a_ij=1; Егер түйін мен тармақ байланыста болса, түйіннен тармақ шықса, теңдік орындалады.a_ij=-1; Егер түйін мен тармақ байланыста болса, түйінге тармақ кірсе, теңдік орындалады. a_ij=0; Егер түйін мен тармақ байланыста болмаса орындалатын теңдік. Матрицаның бағанындағы элементтер қосындысы нөлге тең болады, себебі ол элементтердің біреуі 1, басқасы -1, 0.

Контурлы матрица – Кирхгофтың екінші заңына құрылған теңдеулердің коэффиценттерінің таблицасы. Контурлы В матрицаның жолы контур санымен, ал бағаны схема тармағының санымен сипатталады. В матрицасының элементтерін b_ij деп белгілейік.

b_ij=1; Егер контурға тармақ кірсе және олардың тағыттары бірдей болса, теңдік орындалады.b_ij=-1; Егер контурда тармақ болса, бағыттары қарсы болса, теңдік орындалады.b_ij=0; Егер контурдың құрамында тармақ болмаса орындалатын теңдік. Басты контурға жазылған В матрицасы бас контур матрицасы деп аталады. Сондықтан контурдың бағытын белгілеу үшін байланыс тармақтарының бағыттарын 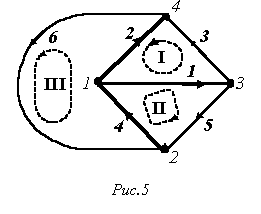алады.

2-1-4 тармақтарының көмегімен алынған талдардан В матрицасының коэффиценттерін аламыз.

Қисындық матрица – қисындар үшін бірінші Кирхгоф заңынан құралған теңдеулердің коэффиценттерінің таблицасы. Жолдары қисындар санымен, бағандары графтың тармақтар санымен сипатталады. Бұл матрицаны Q матрицасы деп белгілейік. Оның элементтері q_ij болсын.

Басты қисындардан құралған матрица басты қисын матрицасы деп аталады. Матрицаның жолдар саны тәуелсіз қисындар санына тең.

q_ij=1; Егер тармақ қисын құрамына енсе, бағыттары бірдей болса, теңдік орындалады.

q_ij=-1; Егер бағыттары қарама қарсы болса, теңдік орындалады.

q_ij=0; Егер тармақ қисын құрамына кірмесе орындалатын теңдік.

Ом заңы.

1827 жылы неміс физигі Г. Ом бірнеше тәжірибе өткізіп, электр тогының негізгі заңын шығарды: «Гальваникалық тізбектің ток шамасы, кернеуге тура пропорционал және кедергіге кері пропорционал».

1 I R 2

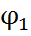
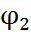
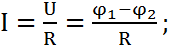Тізбек бөлігі үшін Ом заңы

Толық тізбек үшін Ом заңы былай анықталады:

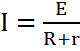, мұндағы 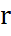- ішкі кедергі.

ЭҚК-сі бар тізбек саласының Ом заңы

Резистор және ЭҚК-сы бар тізбек саласын қарастырайық:

a R b E I c

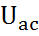
Бұл жағдайда Ом заңы орындалады: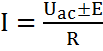

Кирхгоф заңдары.

1) Кирхгоф заңдары тармақталған электр тізбектегі ток пен кернеудің байланысын орнатады. Кирхгофтың бірінші заңының негізі – зарядтың сақталу заңы болып табылады: тізбектің кез келген түйініндегі токтардың I_i алгебралық қосындысы нөлге тең:

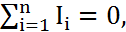(1)

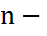түйіндегі токтар саны.

I₁ I₂

I₃

I₅ I₄

Мысалы, жоғарыдағы суреттегі электр тізбегінің түйініне бірінші заң бойынша теңдеуді мына түрде жазуға болады:

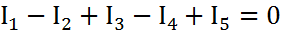
Түйінге бағытталған токтарды оң деп аламыз. Кирхгофтың екінші заңы былайша тұжырымдалады: күрделі электр тізбектегі кез келген тұйықталған контурда, контур кедергісіндегі барлық кернеу шығындарын алгебралық қосындысы, осы контурдағы қорек көзі ЭҚК-нің алгебралық қосындыларына тең, яғни:

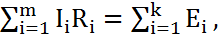(2)

m – тұйықталған контурдағы тармақтар саны, I_i, R_i – і тармағының тогы мен кедергісі, k – ЭҚК саны.

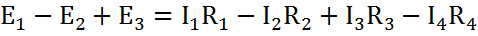
Белгілердегі ескерту:

1) ЭҚК оң, егер оның бағыты таңдап алынған контурдың аралау бағытымен сәйкес болса;

2) Резистордағы кернеудің шығыны ток бағыты аралау бағытымен сәйкес болса оң болады.

6,Қарапайым және күрделі тұрақты тоқтың сызықты тізбектерін талдау әдістері.

Контурлы ток әдісі.

Контурлық токтар әдісі біріктіріліп шешілетін теңдеулердің санын K=n-m-n_тк­­+1 шамасына дейін азайтуға мүмкіндік береді және Кирхгофтың екінші заңын қолдануға негізделген .

Әуелі n_тк­­=0 , яғни ток көзі болмаған жағдайда , тізбектің схемасын есептеу үшін қолданылатын әдістің мәніне тоқталайық:

1) K=n-m+1 контурларды және әрқайсысы тиісті контурдың барлық элементтері арқылы жүретін , контурлық токтардың оң бағытын таңдаймыз .

Планарлық схема үшін(яғни тармақтары бірін-бірі кеспейтін жазықтықтағы кескіннің мүмкіндігі), К тәуелсіз контурларды бөліп алудың жеткілікті шарты , олардың әр қайсысына тек осы контурға тән болатын кем дегенде бір тармақ болуы керек ;

2)Кирхгофтың екінші заңы бойынша, К тәуелсіз контурлар үшін теідеулер құрамыз . Ол теңдеулерді біріктіріп шешкенде контурлардағы барлық контурлық токтар анықталады ;

3)әрбір тармақтың тогын Кирхгофтың бірінші заңы бойынша , тармақтарға тиісті контурлық токтарды алгебралық қосындылау арқылы анықтаймыз .

R1

R2

E1

E2

E4

E3

R5

R4

R3

R6

I1

I2

I4

I5

I3

I6

I11

I22

I33

Мысал ретінде жоғарыдағы суретті келтірейік . Онда n=6 тармақ, m=4 түйін және K=n-m+1=6-4+1=3 контур бар суретте көрсетілгендей 1-3 тәуелсіз контурларды және олардағы I₁₁, I₂₂ , I₃₃ токтардың оң бағытын анықтаймыз. Тармақтағы токтан ерекше олардың әрқайсысындағы токты контурдың нөмірі арқылы екі іиндекспен белгілейміз. Кирхгофтың екінші заңы бойынша теңдеу құрамыз:

1-контур

(R₁+R₄+R₆)I₁₁- R₆I₂₂ +R₄I₃₃= E₁-E₄

2-контур)

-R₆I₁₁ +(R₂+R₅+R₆)I₂₂ +R₅I₃₃= E₂ (1)

3-контур

R₄I₁₁ +R₅I₂₂+(R₃+R₄+R₅)I₃₃ = E₃-E₄

(1) теңдеулер жүйесінен ауыстыру әдісі немесе ЭЕМ-да сандық әдісті пайдалану арқылы I₁₁, I₂₂ , I₃₃ токтарын анықтайды. Тармақтағы токтарды (суреттегі) Кирхгофтың бірінші заңы бойынша табамыз:

I₁=I₁₁ , I₂=I₂₂, I₃=I₃₃, I₄=-I₁₁-I₃₃, I₅=I₂₂+I₃₃,

I₆=I₁₁-I₂₂

Беттесу әдісі.

ЭҚК көздері бар сызықты электрлік тізбектердегі контурлық токтар контурлық ЭҚК сызықты функциясы болып келеді. Шынымен, (1.20) –дан j контурының контурлық тогы үшін жалпы өрнегі мынадай

,

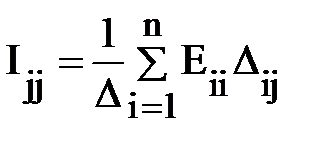мұндағы E_ii – тармақтың ЭҚК кіретін контурлық ЭҚК.

Контурларды j тармағы j контурына кіргендей етіп қабылдаймыз. Онда осы тармақтын тогы сәйкес келетін контурлық токқа тең болады. Егер контурлық ЭҚК тармақтардағы ЭҚК арқылы шығарсақ, онда

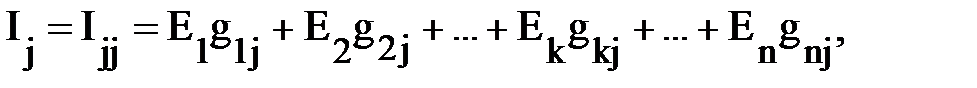
мұндағы E₁, E₂,…E_n – тармақтардағы ЭҚК;

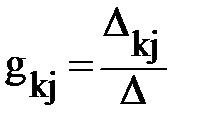өткізгіштіктердің өлшеміне ие.

(1.42) теңдеуіне сәйкес j тармағының тогы тізбектің әр ЭҚК жекелеп тудырылған токтардың алгебралық қосындысына тең. Бұл беттесу принципі тек қана сызықты тізбектер үшін орындалады.

Беттесу әдісі бойынша есептеу алгоритмі:

- басқа қорек көздердің ішкі кедергілерін қалдырып өздерін схемадан алып тастайды да жекелеп әр ЭҚК (ток) көзінен тармақтардағы токтарды (құрама токтарды) кезектеп есептейді;

- тармақтардағы токтар құрама токтардың алгебралық қосындысы сияқты анықталады;

Екі түйін әдісі.

Параллель қосылған кезде екі түйін арасында бірнеше тармақ орналасады, осы кезде барлық тармақтардағы кернеу бірдей болады .

b

I2

I3

r1

r2

r3

r4

r5

E2

UJ

Uab

I1

a

E1

J

φ_b = 0 – базистік түйін деп аламыз, ал "а" түйінінің φ_а потенциалы белгісіз болады. φ_а потенциалын анықтау үшін теңдеу келесідей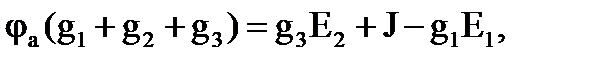

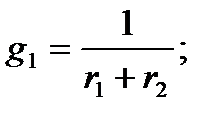
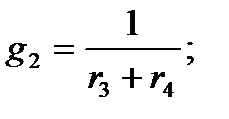
мұндағы 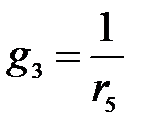- тармақтардың өткізгіштіктері.Схеманың екі түйіні арасындағы кернеу келесі формула бойынша анықталады

.

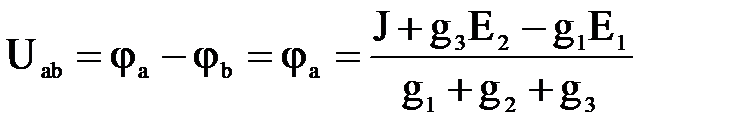U_ab кернеуінің мәнін біліп Ом заңы бойынша тармақтардағы токтарды анықтаймыз (токтардың оң бағыты ерікті алынады)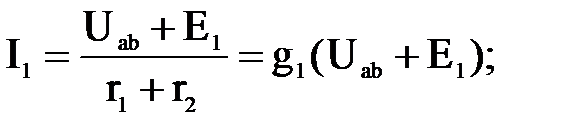

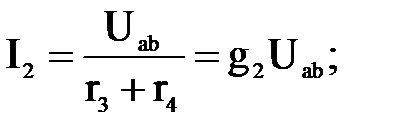
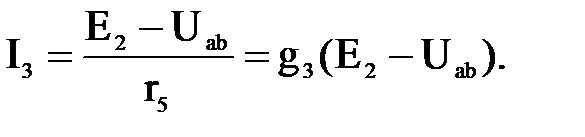
Осы формулаларға U_ab кернеу мен ЭҚК «плюс» таңбасымен кіреді, егер олардың бағыттары тармақтардағы токтармен сәйкес келсе. U_J = φ_a – φ_b = U_ab