Соединение фаз генератора и приемника треугольником

Вторым основополагающим способом соединения является соединение типа «треугольник-треугольник» (рис.4.6).

Для соединения треугольником существует следующее соотношение:

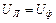93(4.4)

Установим взаимосвязь между фазными и линейными токами:

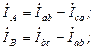
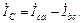
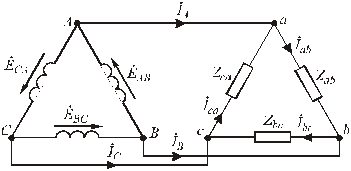
Рис.4.6. Соединение «треугольник-треугольник»

Построим векторную диаграмму токов и напряжений приемника (рис.4.7).

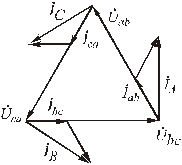
Рис.4.7. Векторная диаграмма трехфазной цепи при соединении приемников «треугольником» при симметричной нагрузке

Рассмотрев любой треугольник токов, можно аналогично напряжениям при соединении звездой, сделать вывод (только для симметричной нагрузки):

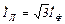94(4.5)

Помимо вышеназванных существуют и комбинированные способы соединения: «звезда-треугольник», «треугольник-звезда».

Режимы работы трехфазных цепей

4.3.1. Соединение «звезда-звезда» с нулевым проводом и без нулевого провода

Поскольку трехфазные цепи являются совокупностью однофазных цепей, то для их расчета используются все рассмотренные методы, в том числе и комплексный метод расчета. А значит, расчет трехфазных цепей можно иллюстрировать построением векторных диаграмм токов нагрузки и топографических диаграмм напряжений.

Наиболее рациональным методом расчета цепи может считаться метод двух узлов. Для выбранных положительных направлений напря­жений и токов на схеме (рис.4.8), составим соответствующую систему уравнений для расчета токов:

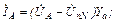
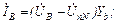95(4.6)

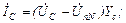
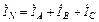; 96(4.7)

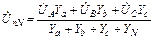; 97(4.8)

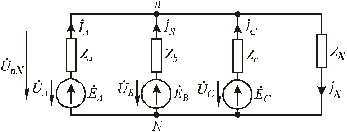
Рис.4.8. Соединение фаз генератора и приемника
по схеме «четырехпроводная звезда»

Симметричная нагрузка

Нагрузка считается симметричной, если комплексные сопротивления ее фаз равны: Z_a = Z_b = Z_c.

а) четырехпроводная звезда

Для простоты в качестве сопротивлений фаз нагрузки будем рассматривать активные сопротивления (Z_a = Z_b = Z_c = Z_ф = R_ф). Наличие нулевого провода делает одинаковыми потенциалы узлов N и n (Y_N = ¥), значит U_nN = 0. При этом фазные токи равны, а фазные напряжения на нагрузке будут полностью повторять фазные напряжения генератора. Для фазы А:

.

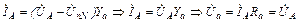Аналогично для фаз В и С:

;

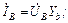
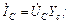
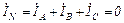Исходя из сказанного, построим топографическую диаграмму фазных напряжений и векторную диаграмму токов (рис.4.9).

в) трехпроводная звезда

Z_N = ¥; Y_N = 0;

.

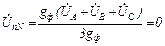Поэтому, как и в четырехпроводной схеме, фазы приемника работают независимо друг от друга и нулевой провод не нужен. Диаграмма в данном случае будет абсолютно той же самой.

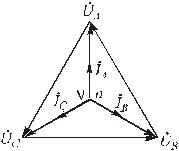
Рис.4.9. Векторная диаграмма для симметричной нагрузки
в трех- и четырехпроводной схеме

Несимметричная нагрузка

Пусть R_a ¹ R_b = R_c;

а) четырехпроводная звезда

;

;

;

;

.

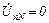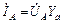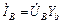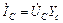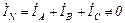На векторно-топографической диаграмме токов и напряжений (рис.4.10) показано сложение токов.

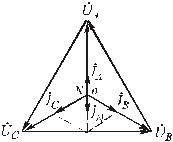
Рис.4.10. Векторно-топографическая диаграмма для несимметричной нагрузки

Б) трехпроводная звезда

Из-за неравенства проводимостей ветвей 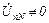, то есть между точками n и N появляется некоторая разность потенциалов, так называемое смещение нейтрали. При этом фазные напряжения на нагрузках уже не будут повторять систему фазных напряжений генератора. Поэтому задача сводится к задаче определения положения точки n на комплексной плоскости относительно N. Для его определения можно воспользоваться формулой узлового напряжения и теоретически ее рассчитать. Однако можно это сделать, основываясь на экспериментальных данных, суть которых состоит в следующем: производят измерения реальных значений напряжений на фазах нагрузки; в выбранном масштабе для напряжений проводят дуги окружностей радиусами, равными измеренным фазным напряжениям, из точек A, B, C. Точка пересечения этих трех дуг и даст искомое местоположение точки n внутри треугольника, ограниченного линейными напряжениями (рис.4.11).

Соединив точки n и N отрезком, получим смещение нейтрали. По найденным фазным напряжениям приемника направляем векторы токов. Должно выполняться равенство:

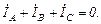
По результатам выполненных построений можно сделать главный вывод: если заведомо известно, что нагрузка несимметрич­на или может таковою стать, необходимо использовать четырехпроводную схему.

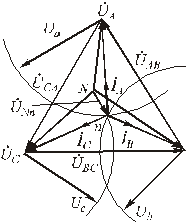
Рис.4.11. Определение смещения нулевой точки

Обрыв фазы

R_a = ¥; R_b = R_c;