Геометричні характеристики поперечного перерізу
Здатність матеріала чинити опір деформаціям залежить від його фізичних та геометричних характеристик.
До геометричних характеристик тіла відноситься його довжина та параметри поперечного перерізу. До параметрів, що характеризують поперечний переріз належать:
- площа поперечного перерізу;
- статичний момент площі;
- момент інерції
Розглянемо довільну конфігурацію поперечного перерізу тіла (рис.22) Виділимо елемент площі 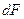 з координатами
з координатами 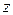 ,
, 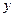 . Добуток елемента площі
. Добуток елемента площі 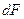 на відстань від центра ваги цієї площі до осі, називається статичним моментом площі цього елемента відносно розглядуваної вісі.
на відстань від центра ваги цієї площі до осі, називається статичним моментом площі цього елемента відносно розглядуваної вісі.
 Рис.22 Рис.22 | 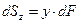 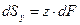 Підсумувавши такі добутки по всій площі фігури отримаємо статичні моменти поперечного перерізу відносно осей Підсумувавши такі добутки по всій площі фігури отримаємо статичні моменти поперечного перерізу відносно осей 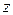 та та 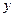 . . 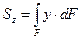 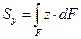 |
Статичні моменти площі поперечного перерізу відносно центральних осей (осей, що проходять через центр ваги) дорівнюють нулю.
Якщо по аналогії із статичним моментом, елементи площі будемо множити на квадрат відстані до розглядуваної осі то отримаємо визначення момента інерції елемента площі.
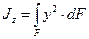
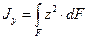
Приклад
Визначимо статичні моменти та моменти інерції заданої площі поперечного перерізу тіла у вигляді прямокутника відносно осей 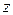 та
та 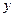 (розміри задані в сантиметрах).
(розміри задані в сантиметрах).
 | Статичні моменти площі: 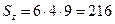 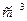 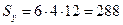 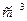 Моменти інерції: Моменти інерції: 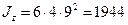 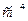 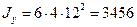 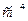 |
Внутрішні зусилля
Між сусідніми точками тіла (кристалами, молекулами, атомами) завжди виникають певні сили взаємодії (внутрішні сили). Дія зовнішніх сил призводит до виникнення додаткових внутрішніх зусиль, які намагаются зберегти тіло як єдине ціле, і протидіють всякому намаганню змінити розташування точок тіла (деформуванню тіла). Зовнішні сили навпаки, завжди намагаються викликати деформацію тіла, змінити взаємне розташування точок.
Для виявлення та подальшого обчислення внутрішніх зусиль широкого застосування набув метод перерізів. Розглянемо тіло що знаходится в рівновазі під дією зовнішніх сил та реакцій вязей. У місці де ми хочемо визначити внутрішні зусилля уявно проведемо поперечний переріз (рис.23). Внаслідок цього тіло розділиться на 2 частини А і В. При цьому сам переріз буде мати 2 сторони: одну, що належить частині А, і другу що належить частині В (рис.24).
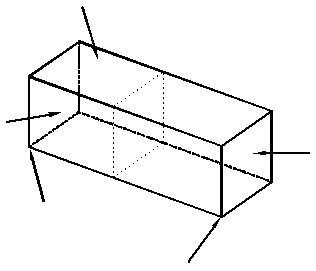
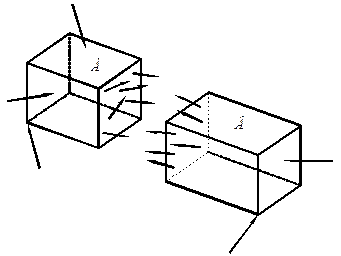
Рис.23 Рис.24
В кожній точці з обох сторін перерізу будуть діяти сили взаємодії. Причому внутрішні сили, що будуть діяти в поперечному перерізі на стороні А у відповідності з 3 законом Ньютона рівні за величиною і протилежні за напрямком внутрішнім силам діючим в поперечному перерізі на стороні В.
Напрямок внутрішніх зусиль може бути довільним. Для проведення розрахунів будь-яке довільно спрямоване внутрішнє зусилля може бути представленим дією 2 складових цього зусилля. Напрямок 1 складової буде співпадати з напрямком нормалі до поперечного перерізу. 2 складову спрямуємо вздовж вісі перпендикулярної до нормалі (рис.25).
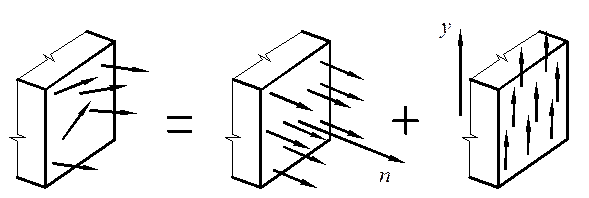
Рис.25
Сумма перших складових діючих на одиничній площі перерізу називаєтся нормальним напруженням 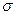 . Сума других складових діючих на одиничній площі перерізу називаєтся дотичним напруженням
. Сума других складових діючих на одиничній площі перерізу називаєтся дотичним напруженням 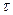 . Напруження вимірюються в паскалях (
. Напруження вимірюються в паскалях ( 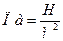 ).
).
В загальному випадку завантаження важко визначити закон розподілу внутрішніх зусиль в поперечному перерізі. Однак користуючись рівняннями рівноваги можна визначити їх рівнодіючі сили. Таким чином дія внутрішніх зусиль на поперечний переріз тіла може бути представленою дією 3 сил, що прикладені в центрі ваги поперечного перерізу (рис.26):
- повздовжньої сили N,
- поперечної сили Q,
- згинального момента M.
Повздовжня сила N спрямована вздовж осі стержня і викликає його повздовжню деформацію (стиск або розтяг). Вона дорівнює сумі проекцій всіх внутрішніх зусиль, діючих в перерізі на нормаль до перерізу.
Поперечна сила Q спрямована поперек осі стержня і являє собою суму проекцій всіх внутрішніх зусиль діючих в перерізі на нормаль до перерізу.
Згинальний момент являє собою суму моментів всіх внутрішніх зусиль відносно центральної вісі перерізу.

Рис.26
Зусилля N,Q,M, що прикладені в поперечному перерізі частини тіла А дорівнюють аналогічним зусиллям прикладеним в поперечному перерізі частини тіла В, але з протилежними напрямками.
Практичне обчислення N, Q та M виконується виходячи з рівнянь рівноваги. Зусилля N чисельно дорівнює алгебраїчній сумі на вісь стержня (на рис. 26 вісь x) всіх зовнішніх сил, що діють в частині тіла А або в частині тіла В. Аналогічно для визначення сили Q беруть суму проекцій всіх сил на вісь ортогональну до вісі стержня (на рис. 26 вісь y).
Якщо в поперечних перерізах стержня виникають лише повздовжні сили N, а Q та M дорівнюють нулю, то в межах поперечного перерізу в усіх точках нормальні напруження будуть однаковими, а дотичні напруження дорівнюватимуть нулю.
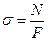 ,
,
де F - площа поперечного перерізу тіла.
Якщо в поперечних перерізах тіла виникають лише деформації згину ( 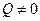 ,
, 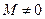 , а
, а 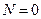 ) нормальні і дотичні напруження будуть визначатися за формулами:
) нормальні і дотичні напруження будуть визначатися за формулами:
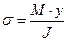 ,
, 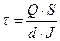
де y – координата вздовж осі y, що визначає розташування точки визначення напруження;
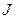 - момент інерції площі поперечного перерізу відносно центральної осі поперечного перерізу навколо якої діє момент М (на рис.26 - вісь z);
- момент інерції площі поперечного перерізу відносно центральної осі поперечного перерізу навколо якої діє момент М (на рис.26 - вісь z);
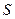 - статичний момент площі частини поперечного перерізу, яка знаходиться вище координати y
- статичний момент площі частини поперечного перерізу, яка знаходиться вище координати y
d – ширина поперечного перерізу в місці визначення напруження
Види деформацій
Внаслідок дії на конструкції різного виду навантажень, вони деформуються, тобто змінюють свою первісну форму. Розрізняють наступні види деформацій:
- розтягу та стиску;
- зсуву або зрізу;
- кручення;
- згину.
Деформації розтягу або стиску виникають, наприклад, у випадку, коли до стержня вздовж його вісі прикладені протилежно спрямовані сили (рис.27,а). При цьому відбувається поступове переміщення перерізів вздовж осі стержня. При розтязі його довжина збільшується, при стиску – зменшується. Відношення величини приросту або укорочення довжини стержня до його початкової довжини називають відносною повздовжньою деформацією стержня:
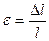
Розтяг (стиск) матеріала в одному напрямку супроводжується зменшенням (збільшенням) розмірів по іншим напрямкам, перпендикулярним напрямку розтягу (стиску) (рис.27,б). Відносна поперечна деформація буде визначатися за формулою:
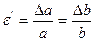 .
.
Відношення відносної поперечної деформації до повздовжньої визначає коефіцієнт лінійної деформації (коефіцієнт Пуасона):
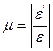 .
.
Для різних матеріалів коефіцієнт Пуасона змінюється в межах : 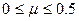 .
.
В умовах розтягу або стиску зв'язок між напруженнями та деформаціями описується на основі закону Гука:
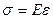 ,
,
де Е 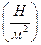 – модуль пружності, що характеризує фізичні властивості матеріала.
– модуль пружності, що характеризує фізичні властивості матеріала.
Для ізотропних матеріалів, параметри Е та 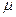 повністю характеризують їх пружні властивості.
повністю характеризують їх пружні властивості.
В будівництві деформацій стиску та розтягу зазнають колони, стержні ферм т.і. конструкції.

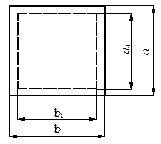
а б
Рис. 27
Зсув, або зріз, виникає, коли зовнішні сили зміщують два паралельних плоских переріза стержня одне відносно іншого при незмінній відстані між ними. Величина зсуву 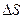 називається абсолютним зсувом (рис.28). Відношення абсолютного зсуву до відстані між поверхнями що зміщуються (тангенс кута
називається абсолютним зсувом (рис.28). Відношення абсолютного зсуву до відстані між поверхнями що зміщуються (тангенс кута 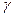 ) називають відносним зсувом. Внаслідок малості кута
) називають відносним зсувом. Внаслідок малості кута 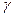 можна вважати:
можна вважати:
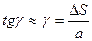
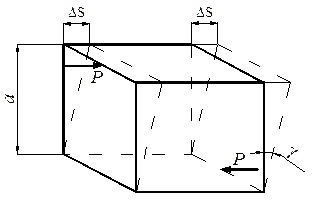
Рис.28
Кручення виникає при дії на стержень зовнішніх сил, утворюючих момент відносно його вісі (рис.29). Деформація кручення супроводжується повертанням поперечних перерізів стержня один відносно іншого навколо його вісі. Кут повертання одного перерізу стержня відносно іншого, які знаходяться на відстані 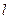 , називають кутом закручування на відстані
, називають кутом закручування на відстані 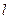 . Відношення кута закручування
. Відношення кута закручування 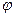 до довжини
до довжини 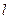 називають відносним кутом закручування:
називають відносним кутом закручування:
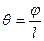
.

Рис.29
Деформації згину полягають у зміні кривизни осі стержня (рис.30). В прямих стержнях переміщення точок, що спрямовані перпендикулярно до початкового положення вісі називають прогинами 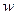 . Найбільша величина прогину позначається
. Найбільша величина прогину позначається 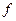 . Кути повороту перерізів відносно своїх початкових положень позначають
. Кути повороту перерізів відносно своїх початкових положень позначають 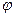 . На згин працюють перекриття будівель.
. На згин працюють перекриття будівель.
В багатьох випадках деформації конструкцій являють собою сполучення вищеназваних видів деформацій

Рис.30
