Сила – постоянная величина

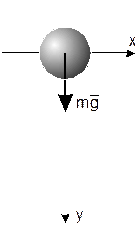Тело массой m падает без начальной скорости с некоторой высоты. Определить какое расстояние пройдет тело через t секунд.

Решение.

, , ,

, , , ,

,

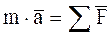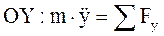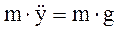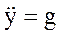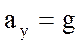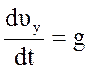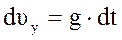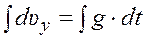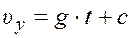
При t = 0: , ,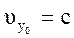

,

,

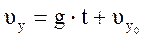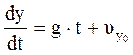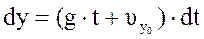
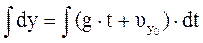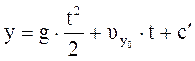
При t = 0, , ,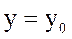

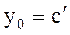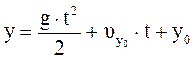
При ,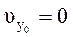

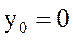
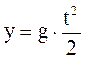
Сила зависит от расстояния.

Материальная точка массой m = 20 кг отталкивают от некоторого неподвижного центра с силой обратно пропорциональной кубу расстояния и направленной вдоль оси X 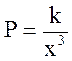. При этом 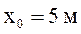, , 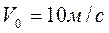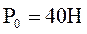. Определить закон движения .

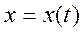Решение.

Найдем коэффициент пропорциональности из начального условия:

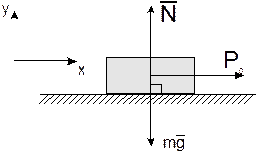
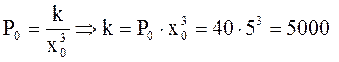Н/м³

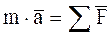
ОХ: ,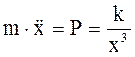

;

,

,

,

,

, .

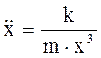
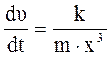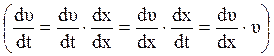
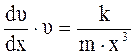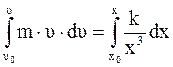
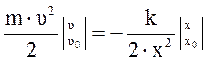
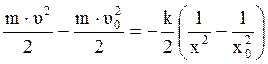
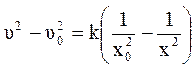
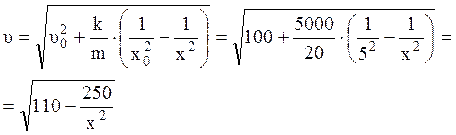
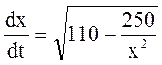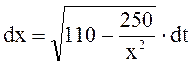
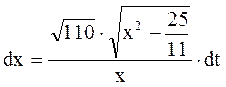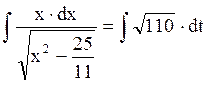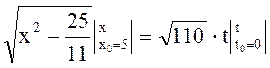
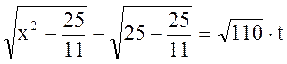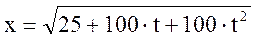Сила зависит от скорости.

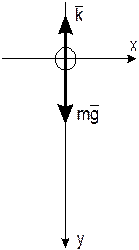Тело массой m падает с некоторой высоты. Точка начала движения совпадает с началом отсчета 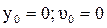. Сопротивление воздуха задано функцией 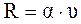, где 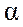- коэффициент пропорциональности 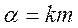. Определить скорость и закон движения тела.

Решение.

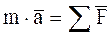
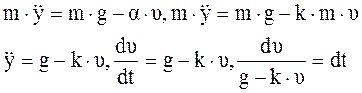
Вводим новый коэффициент:

,

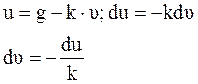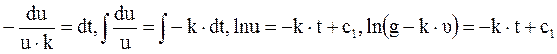
При :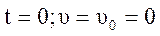

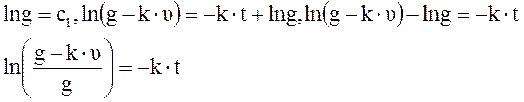
Потенцируем правую и левую часть уравнения

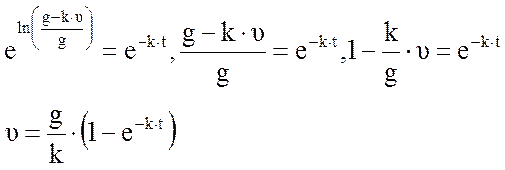
При времени 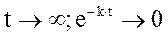и скорость, таким образом, при долгом падении стремится к постоянной величине: .

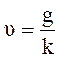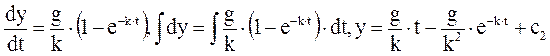
При :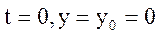

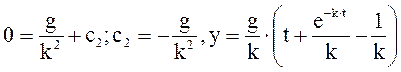
Сила зависит от времени.

Тело массой m из состояния покоя начинает двигаться под действием силы 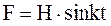. Сила F параллельна оси ОХ. Определить закон движения тела.

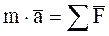, ОХ: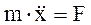

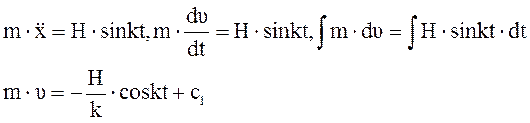
При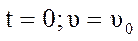

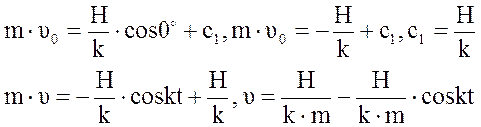
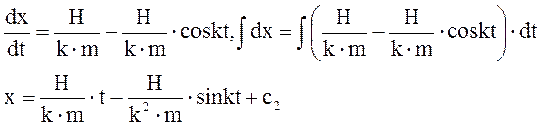
При t = 0, x = x₀:

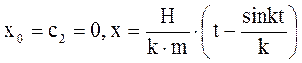
3.2.3. КОЛЕБАНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ

1. Основные понятия

Колебания являются одним из наиболее распространенных видов движения и имеет широкое распространение в природе и технике. Несмотря на различную физическую природу, основные законы электромагнитных и звуковых колебаний те же, что и для механических колебаний. Изучение их объединяется в общей теории колебаний, представляющей в настоящее время самостоятельную, обширную и сложную отрасль механики. Ниже мы будем рассматривать лишь простейшие случаи прямолинейного колебательного движения материальной точки.

Общим признаком всех колебательных движений является их многократная повторяемость через определенные промежутки времени. Колебательное движение материальной точки происходит при условии наличия восстанавливающей силы.

Восстанавливающая сила – это сила, стремящаяся вернуть точку в положение равновесия.

Данная сила чаще всего зависит от величины отклонения точки от положения равновесия и направлена к положению равновесия. Проведем через некоторую точку M и положение равновесия O прямую Ox, приняв положение равновесия за начало системы отсчета (рис.3.5).

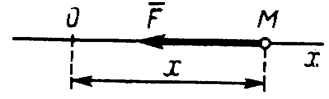
Рис.3.5

Тогда проекция восстанавливающей силы на ось Ox может быть найдена из выражения F_x=-c·x,

где c – коэффициент пропорциональности.

Кроме восстанавливающей силы при колебании на точку может действовать также возмущающая сила, т.е. такая сила, которая зависит от времени. Обычно в качестве возмущающей силы рассматривают силу, проекция которой на ось Ox определяется следующим выражением:

,

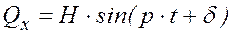где H, p и δ – некоторые постоянные величины.

Наконец, еще одной силой, которую обычно могут рассматривать при колебаниях, является сила сопротивления. Обычно эту силу рассматривают как функцию скорости точки и называют силой вязкого трения. При этом ее проекция на ось Ox определяется из выражения

,

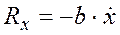где b – коэффициент пропорциональности.

В зависимости от наличия восстанавливающей силы, возмущающей силы или силы сопротивления колебания материальной точки классифицируются следующим образом.

1) свободные колебания

2) свободные колебания при вязком сопротивлении (затухающие колебания)

3) вынужденные колебания