Дәріс сабағы. Сызықтық алгебралық теңдеулер жүйесі
Кері матрица. Анықтама.А матрицасының кері матрицасы деп, 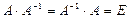 теңдіктерін қанағаттандыратын
теңдіктерін қанағаттандыратын 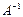 матрицасын айтады, мұндағы Е-бірлік матрица.
матрицасын айтады, мұндағы Е-бірлік матрица.
Анықтауышы нөлге тең емес квадрат матрицаны ерекше емес (нұқсансыз) матрица деп, ал анықтауышы нөлге тең матрицаны ерекше (нұсқанды) матрица деп атайды. Элементтері А матрицасының 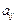 элементтеріне сәйкес
элементтеріне сәйкес 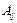 алгебралық толықтауыштары болып келген матрица тіркелген матрица деп аталады.
алгебралық толықтауыштары болып келген матрица тіркелген матрица деп аталады.
Теорема.Ерекше емес квадрат матрицаның бір ғана кері матрицасы болады.
Кері матрица мына формуламен анықталады:
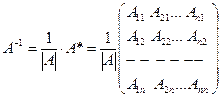 , мұндағы А*- транспонирленген тіркелген матрица.
, мұндағы А*- транспонирленген тіркелген матрица.
Кері матрицаның қасиеттері:
1. 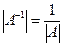 ; 2.
; 2. 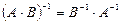 ; 3.
; 3. 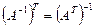 ;
;
4. 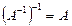 ; 5.
; 5. 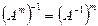 .
.
Сызықтық алгебралық теңдеулер жүйесі. Бізге 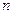 белгісізі бар
белгісізі бар 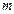 сызықты теңдеулер жүйесі берілсін делік (белгісіздер саны
сызықты теңдеулер жүйесі берілсін делік (белгісіздер саны 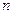 -ге, ал сызықты теңдеулер саны
-ге, ал сызықты теңдеулер саны 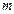 -ге тең):
-ге тең):
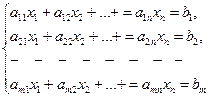 ,
,
мұндағы 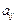 - кез келген нақты сандар, олар осы жүйенің коэффициенттері,
- кез келген нақты сандар, олар осы жүйенің коэффициенттері, 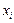 - белгісіз шамалар, ал
- белгісіз шамалар, ал 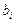 - бос мүшелер деп аталады,
- бос мүшелер деп аталады, 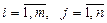 .
.
Берілген сызықты теңдеулер жүйесінің коэффициенттерінен анықталған мына матрица
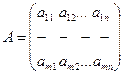
берілген жүйенің негізгі матрицасы деп аталады, ал оның анықтауышы: 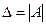 - осы жүйенің анықтауышы деп аталады. Сызықты теңдеулер жүйесінің бос мүшелерін А матрицасының
- осы жүйенің анықтауышы деп аталады. Сызықты теңдеулер жүйесінің бос мүшелерін А матрицасының 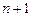 -нші тік жолы етіп алсақ, онда шығатын матрицаны жүйенің кеңейтілген матрицасы деп атайды:
-нші тік жолы етіп алсақ, онда шығатын матрицаны жүйенің кеңейтілген матрицасы деп атайды: 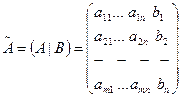 ,
, 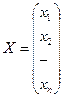 - жүйенің тік жолды белгісіздер матрицасы, ал
- жүйенің тік жолды белгісіздер матрицасы, ал 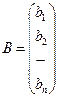 - жүйенің тік жолды бос мүшелер матрицасы. Бос мүшелердің кем дегенде біреуі нөлге тең болмаған жағдайда жүйе біртекті емес деп, ал бос мүшелердің бәрі нөлге тең болса, біртекті жүйе деп аталады.
- жүйенің тік жолды бос мүшелер матрицасы. Бос мүшелердің кем дегенде біреуі нөлге тең болмаған жағдайда жүйе біртекті емес деп, ал бос мүшелердің бәрі нөлге тең болса, біртекті жүйе деп аталады.
Жүйенің барлық теңдеуін тепе-теңдікке айналдыратын 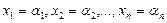 сандары жүйенің шешімі деп аталады. Шешімі бар жүйені үйлесімді, шешімі жоқ жүйені үйлесімсіз деп атайды. Бір ғана шешімі бар жүйені анықталған, ал кем дегенде екі шешімі бар жүйені анықталмаған жүйе деп атайды. Егер
сандары жүйенің шешімі деп аталады. Шешімі бар жүйені үйлесімді, шешімі жоқ жүйені үйлесімсіз деп атайды. Бір ғана шешімі бар жүйені анықталған, ал кем дегенде екі шешімі бар жүйені анықталмаған жүйе деп атайды. Егер 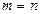 болса, онда жүйе квадратты жүйе деп аталады.
болса, онда жүйе квадратты жүйе деп аталады.
Жүйені шешу әдістері.
Крамер теоремасы (әдісі).Егер біртекті емес квадратты сызықты теңдеулер жүйесінің негізгі матрицасының анықтауышы нөлге тең болмаса, онда ол – анықталған жүйе. Шешімі Крамер формуласымен табылады: 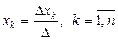 , мұндағы
, мұндағы 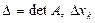 -негізгі матрица анықтауышының
-негізгі матрица анықтауышының 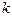 -ншы тік жолының элементтерін жүйенің бос мүшелерімен алмастырғанда шығатын анықтауыш.
-ншы тік жолының элементтерін жүйенің бос мүшелерімен алмастырғанда шығатын анықтауыш.
Мысал. 1) 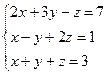 теңдеулер жүйесін шешіңіз. Шешуі:
теңдеулер жүйесін шешіңіз. Шешуі: 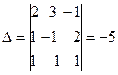
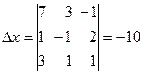
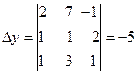
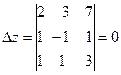
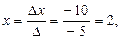
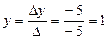
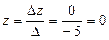
Жауабы: 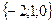 .
.
Матрицалық әдіс. Сызықты алгебралық біртекті емес квадратты теңдеулер жүйесінің негізгі матрицасы ерекше емес болса, онда оны кері матрица әдісімен шешуге болады.
Жүйенің матрицалық теңдеуі: 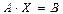 . Сол жағынан теңдеуді
. Сол жағынан теңдеуді 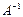 - ге көбейтсек:
- ге көбейтсек: 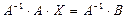 . Бұдан:
. Бұдан: 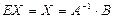 . Осы формуламен Х-матрица –шешімді табу кері матрица әдісі деп аталады.
. Осы формуламен Х-матрица –шешімді табу кері матрица әдісі деп аталады.
Мысал. Жүйені шешіңіз: 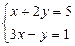 Шешуі:
Шешуі: 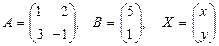
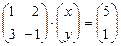 .
. 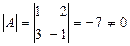
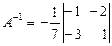
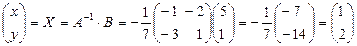
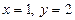 .
.
Гаусс әдісі (элементар түрлендіру әдісі).Бұл әдіспен квадратты емес 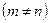 жүйелерді де шешуге болады. Берілген жүйенің
жүйелерді де шешуге болады. Берілген жүйенің 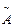 - кеңейтілген матрицасына элементар түрлендірулер жасау арқылы оған эквивалентті трапеция тәріздес немесе үшбұрышты матрица аламыз. Осы алынған матрицаға сәйкес жүйені шешсек, берілген жүйенің шешімдері табылады.
- кеңейтілген матрицасына элементар түрлендірулер жасау арқылы оған эквивалентті трапеция тәріздес немесе үшбұрышты матрица аламыз. Осы алынған матрицаға сәйкес жүйені шешсек, берілген жүйенің шешімдері табылады.
Егер үшбұрышты матрица шықса, онда жүйенің бір ғана шешімі болады (үйлесімді, анықталған), ал, егер трапеция тәріздес матрица шықса, онда жүйенің шексіз көп шешімі болады (үйлесімді, анықталмаған).
Берілген жүйені зерттеу деп оның шешімінің бар-жоғын анықтауды айтады.
Кронекер-Капелли теоремасы (жүйенің үйлесімділік критерийі). Біртекті емес сызықты теңдеулер жүйесі үйлесімді болуы үшін жүйенің негізгі және кеңейтілген матрицаларының рангілері тең болуы, яғни 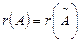 болуы қажетті және жеткілікті.
болуы қажетті және жеткілікті.
Салдарлар:
1. Егер 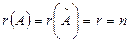 болса, онда жүйенің тек бір ғана шешімі бар (
болса, онда жүйенің тек бір ғана шешімі бар ( 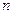 -белгісіздер саны);
-белгісіздер саны);
2. Егер 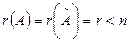 болса, онда жүйенің шексіз көп шешімі бар және ол шешімдер саны
болса, онда жүйенің шексіз көп шешімі бар және ол шешімдер саны 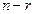 болатын еркін тұрақтыларға (параметрлерге) байланысты;
болатын еркін тұрақтыларға (параметрлерге) байланысты;
3. 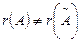 болса, жүйенің шешімі жоқ.
болса, жүйенің шешімі жоқ.
Мысал.Жүйені зерттеп,оның шешімін табыңыз: 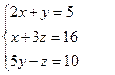
Шешуі. 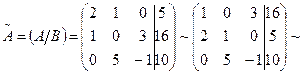
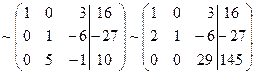
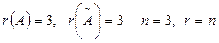 .
.
Ендеше, жүйенің бір ғана шешімі бар.
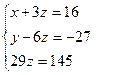
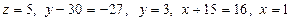
Біртекті сызықтық алгебралық теңдеулер жүйесі:
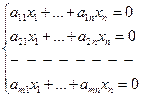 әрқашанда үйлесімді
әрқашанда үйлесімді 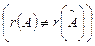 , оның нөлдік (тривиаль) шешімі бар:
, оның нөлдік (тривиаль) шешімі бар: 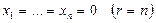 , өйткені оның белгісіздерінің нөлге тең мәндері жүйені әр уақытта да қанағаттандырады. Қандай жағдайда нөлдік емес шешімі болады?
, өйткені оның белгісіздерінің нөлге тең мәндері жүйені әр уақытта да қанағаттандырады. Қандай жағдайда нөлдік емес шешімі болады?
Теорема.Біртекті жүйенің нөлдік емес шешімдері болуы үшін негізгі матрицасының рангісі белгісіздердің санынан кіші болуы 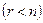 (яғни, негізгі матрицасының анықтауышы
(яғни, негізгі матрицасының анықтауышы 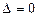 болуы) қажетті және жеткілікті.
болуы) қажетті және жеткілікті.
Біртекті теңдеулер жүйесінің шешімдерінің сызықты комбинациясы да оның шешімі болады. Жүйенің барлық сызықты тәуелсіз шешімдер жүйесін оның іргелі (фундаментальді) шешімдер жүйесі деп атайды. Егер 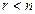 және
және 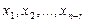 біртекті жүйенің іргелі шешімдері болса, онда оның жалпы шешімі мына формуламен өрнектеледі:
біртекті жүйенің іргелі шешімдері болса, онда оның жалпы шешімі мына формуламен өрнектеледі: 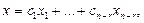 мұндағы
мұндағы 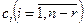 - кез келген сандар.
- кез келген сандар.
Мысалдар.
1. 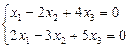 жүйені шешіңіз. Шешуі.
жүйені шешіңіз. Шешуі. 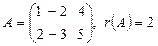 , өйткені
, өйткені
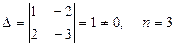 .
. 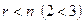 , сондықтан жүйенің шексіз көп шешімі бар.
, сондықтан жүйенің шексіз көп шешімі бар.
Шешімдерді Крамер әдісімен табамыз:
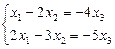 ,
, 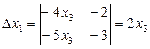 ,
, 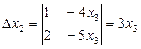
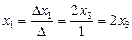 ,
, 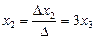 .
. 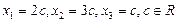 - жалпы шешімдері.
- жалпы шешімдері.
Егер 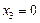 десек, онда бір іргелі шешімді аламыз:
десек, онда бір іргелі шешімді аламыз: 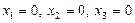 . Егер
. Егер 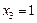 десек, онда екінші іргелі шешімді табамыз:
десек, онда екінші іргелі шешімді табамыз: 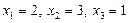 , т.с.с.
, т.с.с.
2. 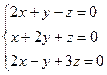 жүйені шешіңіз. Шешуі.
жүйені шешіңіз. Шешуі. 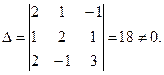
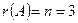
Сондықтан, тек жалғыз нөлдік шешімі болады: 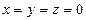 .
.
Бақылау сұрақтары:
1. Сызықты алгебралық теңдеулер жүйесін шешудің қандай әдістері бар?
2. Үйлесімді немесе үйлесімсіз жүйелер деп қандай жүйелерді айтамыз?
3. Қандай жағдайда біртекті сызықты алгебралық теңдеулер жүйесінің нөлдік емес шешімдері болады?
Негізгі әдебиет: [5], 3 тарау, § 3.1-3.6 (101-124 беттер).
Қосымша әдебиет: [17], 1 тарау, § 1.3, 1.4, 1.6, 1.9 (14-18, 21-26, 38-40 беттер).
