Статистический ряд. Гистограмма

При большом числе наблюдений (порядка сотен) простая статистическая совокупность перестает быть удобной формой записи статистического материала - она становится слишком громоздкой и мало наглядной. Для придания ему большей компактности и наглядности статистический материал должен быть подвергнут дополнительной обработке - строится так называемый «статистический ряд». Предположим, что в нашем распоряжении результаты наблюдений непрерывной случайной величины Х, оформленные в виде простой статистической совокупности. Разделим весь диапазон наблюдённых значений на интервалы или «разряды» и подсчитаем количество значений N_i, приходящееся на каждый i-й разряд. Это число разделим на общее число наблюдений N и найдем частоту, соответствующую данному разряду:

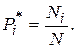
Если разделить частоту на длину соответствующего интервала, то получим статистическую плотность

,

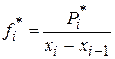являющейся аналогом математической плотности распределения f(x).

Если случайная величина дискретна и целочисленна, то в качестве разрядов обычно принимаются возможные значения этой величины. В этом случае N_i - число реализаций, в которой X=i. Плотность f(x) и 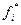для дискретной случайной величины не определяется.

Статистический ряд обычно представляется в виде следующей таблицы:

N интерв.			…	I	…	k
Интервал	x0,x1	x1,x2	…	xi-1,xi	…	xk-1,xk
Число случаев	N1	N2		Ni		Nk
Частота	P1*	P2*	…	Pi*	…	Pk*
Плотость			…		…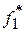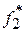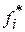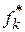

Статистический ряд часто также оформляется графически в виде так называемой гистограммы. Гистограмма строится следующим образом. По оси абсцисс откладываются разряды, и на каждом из разрядов как их основании строится прямоугольник, площадь которого равна частоте данного разряда. Для построения гистограммы нужно частоту каждого разряда разделить на его длину и полученное число взять в качестве высоты прямоугольника. В случае равных по длине разрядов высоты прямоугольников пропорциональны соответствующим частотам.

Из способа построения гистограммы следует, что полная площадь её равна единице.

Пример.1. Приведем гистограмму для длительностей простоя станков с числовым программным управлением (ЧПУ) T_В в связи с восстановлением отказов, построенную по данным статистического ряда, приведенного в ниже следующей таблице. Объем выборки N=193 достаточно большой, поэтому данные приведены в табл.2.3 в сгруппированном виде. Длина интервала 30 мин. Число интервалов k=15.

Таблица 2.3

Статистический ряд простоев станков с ЧПУ

N инт.	Интервал, мин	Число случаев	Частота	Плотность, 1/мин
	0; 30		0.295	0.0098
	30; 60		0.368	0.0122
	60; 90		0.088	0.0029
	90; 120		0.057	0.0019
	120; 150		0.031	0.0010
	150; 180		0.026	0.0009
	180; 210		0.016	0.0005
	210; 240		0.021	0.0007
	240; 270		0.016	0.0005
	270; 300		0.021	0.0007
	300; 330		0.010	0.0003
	330; 360		0.026	0.0009
	360; 390		0.016	0.0005
	390; 420		0.005	0.0002
	420; 450		0.004	0.0002

По данным таблицы построен полигон распределения (рис.2.2) и гистограмма (рис.2.3).

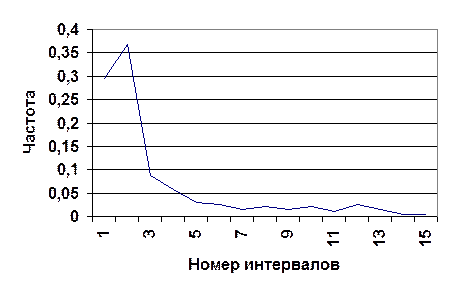
Рис.2.2.Полигон распределения

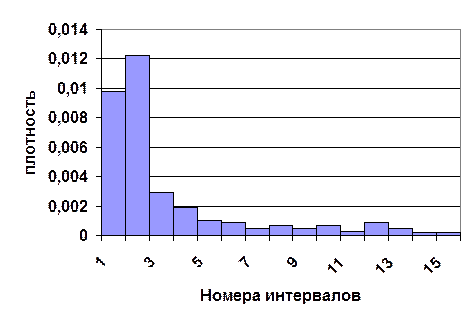
Рис.2.3. Гистограмма статистического распределения.

Очевидно, что при увеличении числа опытов можно выбирать всё более и более мелкие разряды; при этом гистограмма будет всё более приближаться к некоторой кривой, ограничивающей площадь, равную единице. Нетрудно убедиться, что эта кривая представляет собой график плотности распределения величины T_в.

Пользуясь данными статистического ряда, можно приближённо построить и статистическую функцию распределения величины T_в . Построение точной статистической функции распределения с несколькими сотнями скачков во всех наблюденных значениях трудоёмко и себя не оправдывает. Для практики обычно достаточно встроить статистическую функцию распределения по нескольким точкам. В качестве этих точек удобно взять границы разрядов, которые фигурируют в статистическом ряде. В этом случае

.

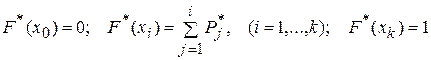Соединяя полученные точки ломаной линией или плавной кривой, получим приближённый график статистической функции распределения. На рис.2.4 приведен такой график статистической функции распределения, построенный по данным табл.2.3.

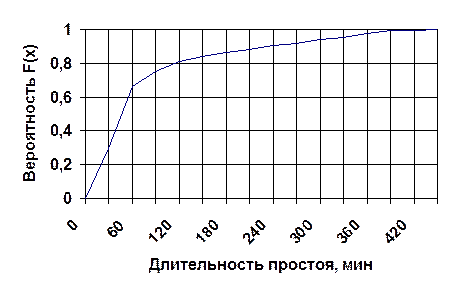
Рис.2.3.График статистической функции распределения.

Если случайная величина дискретна, то в каждом значении X=i, функция распределения 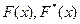терпит скачек на величину 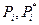соответственно.

2.3.Числовые характеристики распределения

Аналогом математического ожидания в статистике является среднее арифметическое наблюдённых значений случайной величины или статистическое среднее:

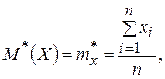
где n – число опытов. Согласно закону больших чисел при неограниченном увеличении числа опытов статистическое среднее приближается к математическому ожиданию. Подобные аналогии существуют для всех числовых характеристик. Будем обозначать их теми же буквами со звёздочкой.

Статистическая дисперсия:

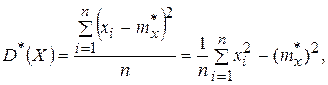
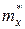- статистическое среднее.

Аналогично определяются статистические начальные и центральные моменты любых порядков:

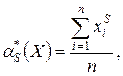
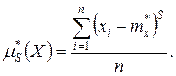
Если число опытов слишком велико и приходится разбивать их на разряды, то получим приближённые формулы:

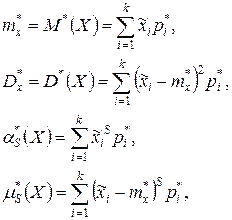
где 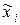- представитель i-го разряда, 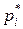- частота i-го разряда, k – число разрядов.

2.4.Оценка параметров распределения

При обработке статистического материала часто приходится решать вопрос о том, как подобрать для данного статистического ряда теоретическую кривую распределения. Такая задача называется задачей выравнивания статистических рядов и состоит в подборе теоретической плавной кривой распределения, наилучшим образом описывающей данное распределение.

Наиболее часто применяется метод наименьших квадратов, при котором сумма квадратов отклонений обращается в минимум. Часто вид случайной функции известен заранее, и нужно лишь определить параметры этой функции. Для решения этой задачи часто применяют различные методы оценки параметров.

Чаще всего используют следующие методы:

· метод моментов;

· метод максимального правдоподобия.

Метод моментов.

Согласно методу моментов параметры распределения выбираются таким образом, чтобы моменты статистического распределения совпадали с соответствующими моментами предполагаемого закона распределения. Если предполагаемый закон распределения случайной величины X имеет один параметр, то он оценивается в результате решения уравнения

.

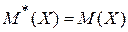Если число параметров 2, то приравниваются первые два момента, в результате получаем систему из следующих двух уравнений для оценки неизвестных параметров распределения:

,

.

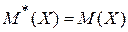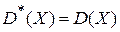Если параметров 3, то приравниваются первые три момента и решают систему уже из трех уравнений и так далее.

Проиллюстрируем применения этого метода на конкретных примерах.

Пример 1.В результате наблюдений за работой станка были получены следующие значения наработки до отказа: 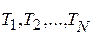. Известно, что наработка на отказ подчиняется показательному распределению с плотностью

.

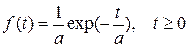Для этого распределения 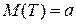, а .

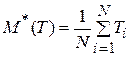Таким образом, получаем следующую формулу для оценки параметра a показательного распределения по опытным данным:

.

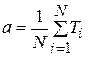Пример 2.В результате контроля размера X партии из N деталей были получены значения 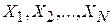. Требуется оценить по этой выборке параметры распределения, в предположении его нормальности. Плотность нормального распределения имеет вид:

.

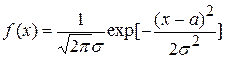Это распределение имеет два параметра 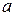и 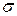, поэтому для их оценки имеем два уравнения, полученные отмеченным выше приравниванием математических ожиданий и дисперсий:

.
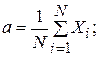
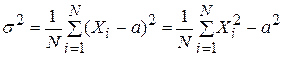