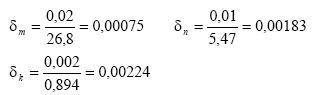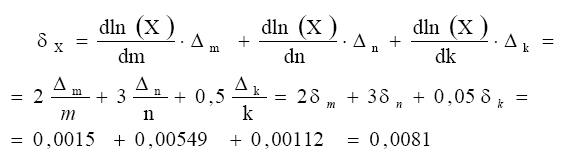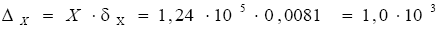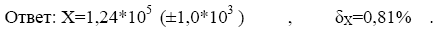Абсолютная и относительная погрешности

Если А - точное значение некоторой величины, a a - известное приближение к нему, то абсолютной погрешностью приближения a числа А называют некоторую величину Δ(a) удовлетворяющую условию:

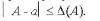
Относительной погрешностью называют некоторую величину δ(А), для которой выполняется условие:

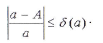
Относительную погрешность часто выражают в процентах.

Информацию о том, что а является приближенным значением числа А с абсолютной погрешностью Δ(а), принято записывать в виде:

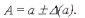
Числа а и Δ(а) записываются с одинаковым количеством знаков после запятой.

Информацию о том, что а является приближенным значением числа А с относительной погрешностью δ(а), записывают в виде:

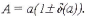
Число δ_α, заведомо не меньшее относительной погрешности называют предельной относительной погрешностью, т.е.

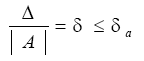
Т.к. на практике A≈ α, то приближенно можно принять, что

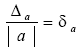
Погрешность функции

Пусть искомая величина Y является функцией параметров a₁, а₂, …, a_n; т.е. Y = Y(a), и известна область G в пространстве переменных a₁, а₂, …, a_n, которой принадлежат параметры. Необходимо получить приближение y к Y и оценить его погрешность.

Если у - приближённое значение величины Y, то предельной абсолютной погрешностью А(у) называют наилучшую при имеющейся информации оценку погрешности величины у:

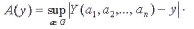
Предельной относительной погрешностью δ(у) называют величину

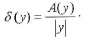
Если задана дифференцируемая функция нескольких независимых переменных 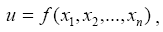то предельная абсолютная погрешность этой функции вызываемая погрешностями аргументов 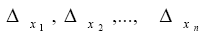оценивается величиной

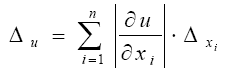
Для оценки предельной относительной погрешности функции имеют место выражения

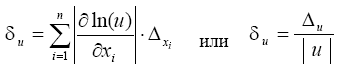
Пример. Оценить абсолютную и относительную погрешности функции 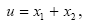считая абсолютные предельные погрешности аргументов известными.

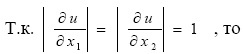
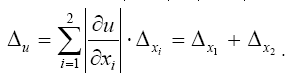
Таким образом, предельная абсолютная погрешность суммы приближенных чисел равна сумме предельных абсолютных погрешностей этих чисел.

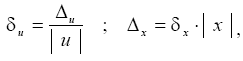тогда если слагаемые одного знака, получаем

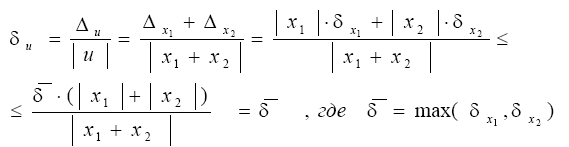
Т.о., если слагаемые одного знака, то предельная относительная погрешность их суммы не превышает наибольшей из предельных относительных погрешностей слагаемых.

Если слагаемые разных знаков, то предельная относительная погрешность суммы вычисляется по формуле

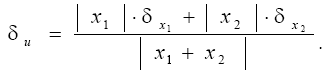
Пример. Оценить абсолютную погрешность функции 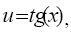считая абсолютную предельную погрешность аргумента известной.

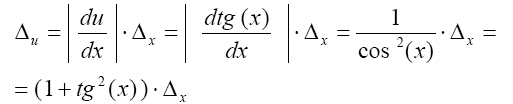
Таким образом, абсолютная погрешность тангенса всегда больше абсолютной погрешности аргумента.

Пример. Вычислить и определить погрешность результата

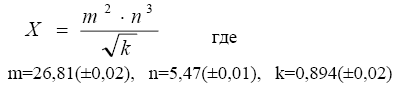
Решение: Произведем вычисления

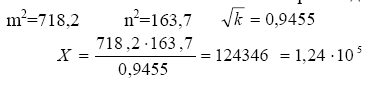
Определим относительные погрешности аргументов