Предмет теории вероятности. Случайные события. Действия над случайными событиями

Марк Аврелий в своих «Размышлениях» писал о двух возможностях: либо мир является огромным хаосом, либо в нем царствует закономерность. И ошибался. Случайное и необходимое выступают вместе. Фундаментальность случайного не приводит к беспорядочности нашего мира.

Наблюдаемые нами события (явления) можно подразделить на следующие три вида: достоверные, невозможные и случайные. Многие явления окружающего мира не всегда находят объяснения в рамках детерминированных законов, поскольку носят случайный (заранее непредсказуемый) характер. Каждое случайное событие есть следствие действия очень многих случайных причин. Невозможно учесть влияние на результат всех этих причин, поскольку число их велико и законы их действия неизвестны. Для математического описания таких явлений удобно считать, что неопределенные факторы имеют случайную природу.

Однако достаточно большое число однородных случайных событий независимо от их конкретной природы подчиняется определенным закономерностям, а именно вероятностным, т.е. хотя для таких событий отсутствует детерминированная регулярность, но имеет место статистическая регулярность, проявляющаяся при рассмотрении массовых явлений.

Теория вероятностей не ставит перед собой задачу предсказать, произойдет единственное событие или нет.

Предметом теории вероятностей является изучение вероятностных закономерностей массовых однородных случайных величин.

Теория вероятностей служит также для обоснования математической и прикладной статистики.

Зарождение теории вероятностей и формирование первых понятий этой ветви математики произошло в середине XVII века, когда Паскаль, Ферма, Бернулли попытались осуществить анализ задач связанных с азартными играми новыми методами.

Общепринятый сегодня аксиоматический подход к вероят­ности был разработан академиком А.Н. Колмогоровым в 1933 г.

Случайным (стохастическим) экспериментом или испытанием называется осуществление какого-либо комплекса условий, который можно практически или мысленно воспроизвести сколь угодно большое число раз.

Явления, происходящие при реализации этого комплекса условий, называются элементарными исходами. Считается, что при проведении случайного эксперимента реализуется только один из возможных элементарных исходов.

Если монету подбросить один раз, то элементарными исходами можно считать выпадение герба (Г) или цифры (Ц). Если случайным экспериментом считать троекратное подбрасывание монеты, то элементарными исходами можно считать следующие: ГГГ, ГГЦ, ГЦГ, ЦГГ, ГЦЦ, ЦГЦ, ЦЦГ, ЦЦЦ.

Между понятиями теории множеств и теории вероятностей устанавливается соответствие. Так, пространством элементарныхисходов называется множество всех элементарных исходов.

Обозначим пространство элементарных исходов буквой W (омега большая); i-й элементарный исход будем обозначать w_i (w– омега малая). Если пространство элементарных исходов содержит n элементарных исходов, то

W=(w₁,w₂ ,...,w_n ).

Для троекратного подбрасывания монеты

W=(ГГГ, ГГЦ, ..., ЦЦЦ).

Если случайный эксперимент – подбрасывание игральной кости, то W=(1, 2, 3, 4, 5, 6).

ЕслиW конечно или счетно, то случайным событиемилипростособытиемназывается любое подмножествоW.Множество называется счетным, если между ним и множеством N натуральных чисел можно установить взаимно-однозначное соответствие.

Приведем примеры событий. Пусть бросается игральная кость, и элементарным исходом считается выпавшее число очков: W=(1, 2, 3, 4, 5, 6). A – событие, заключающееся в том, что выпало четное число очков: А=(2, 4, 6); B –событие, заключающееся в том, что выпало число очков, не меньшее трёх: B=(3, 4, 5, 6).

Говорят, что те исходы, из которых состоит событие А, благоприятствуют событию А.

События удобно изображать в виде рисунка, который называется диаграммой Венна. На рис. 3 пространство элементарных исходов W изображено в виде прямоугольника, а множество элементарных исходов, благоприятствующих событию A, заключено в эллипс.

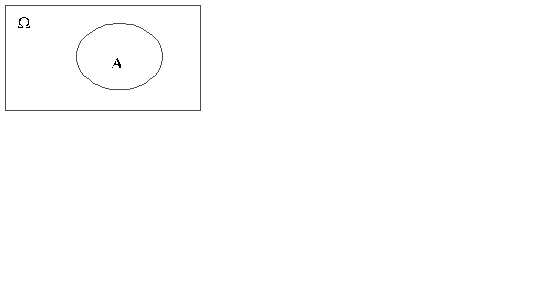
Рис. 3.

Суммой (объединением) двух событийАиB(обозначается A B или А+В) называется событие, состоящее из всех элементарных исходов, влекущих событие А или событие B (рис. 4). Событие A B происходит, если происходит по крайней мере одно из событий А или B.

Пример объединения событий. Пусть два стрелка стреляют в мишень одновременно, и событие А состоит в том, что в мишень попадает 1-й стрелок, а событие B – в том, что в мишень попадает 2-й. Событие A B означает, что мишень поражена, или, иначе, что в мишень попал хотя бы один из стрелков.

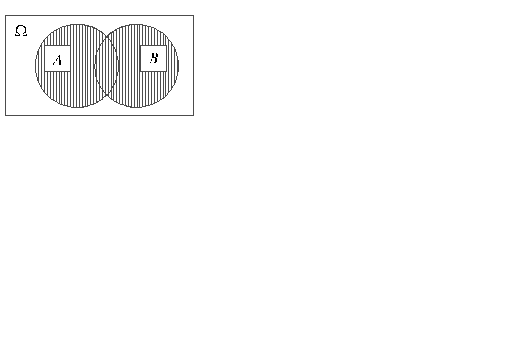
Рис. 4.

Произведением (пересечением) событий А и B называется событие, обозначаемое A∩B или AB,состоящее из всех тех элементарных исходов, из которых следуют оба события А и B. На рис. 5 пересечение множеств, соответствующих событиям А и B, изображено в виде заштрихованной области.

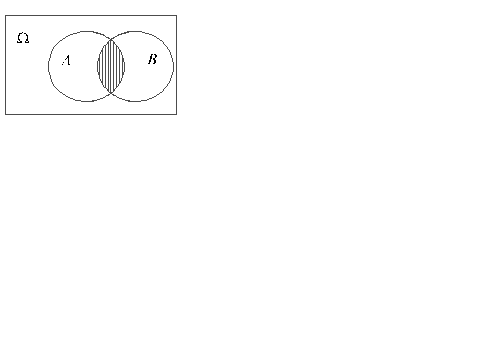
Рис. 5.

В условиях приведенного выше примера событие A∩B заключается в том, что в мишень попали оба стрелка.

Разностью А\B или А–B событий А и B называется событие, состоящее из всех исходов события А, не благоприятствующих событию B. Диаграмма Венна разности событий А и Bизображена на рис. 6. В условиях рассмотренного выше примера событиеА\B заключается в том, что первый стрелок попал в мишень, а второй промахнулся.

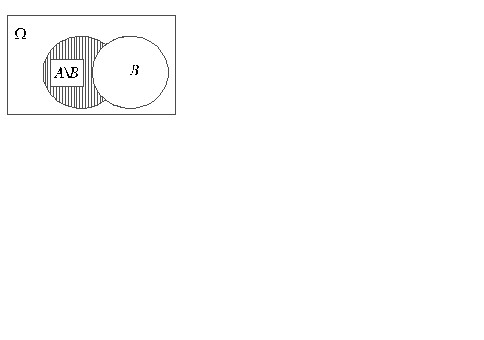
Рис. 6.

СобытиеW называется достоверным, еслионо обязательно происходит в результате случайного эксперимента.

Пустое множество Æ называется невозможнымсобытием.

Событие 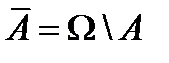называется противоположным событию А или дополнением событияА.

События А и B называются несовместными, если нет исходов, принадлежащих иА и B, то есть A∩B = Æ. На рис. 7 изображены несовместные события А и B.

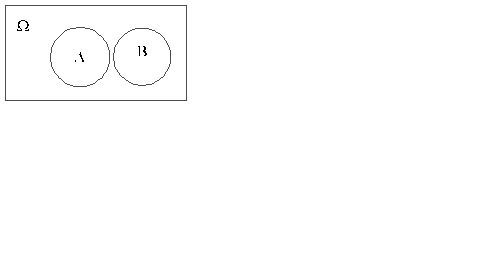
Рис. 7.

Непосредственно из введенных определений следуют равенства:

; ; ; .

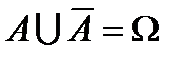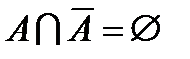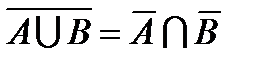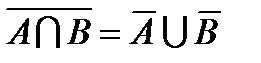На случайные события распространяются свойства множеств. Поэтому можно не делать различия между событиями и соответствующими им множествами.