Теорема Остроградского - Гаусса и ее применение для расчета электростатических полей

В.Г. Лапин

ФИЗИКА

Часть III. Электричество и магнетизм

Утверждено редакционно-издательским

советом университета

в качестве учебного пособия

Нижний Новгород - 2016

ББК 22.3

Л 24

Лапин В.Г. Физика. Часть III. Электричество и магнетизм. Учебное пособие. – Н.Новгород: Нижегород. гос. архит.-строит. ун-т, 2016. – 54 с.

ISBN 5-87941-315-2

В учебном пособии представлен теоретический материал по разделу «Электричество и магнетизм», примеры решения задач с использованием основных законов, составлены варианты контрольных заданий.

ББК 22.3

ISBN 5-87941-315-2 © Лапин В.Г., 2016

© ННГАСУ, 2016

ВВЕДЕНИЕ

Существует две формы существования материи – вещество и поле.

Вещество – это такая форма, когда материя локализована и можно выделить определенный материальный вещественный объект.

Известно, что все материальные объекты взаимодействуют друг с другом. Векторной характеристикой воздействия материальных тел, как мы знаем из механики, является сила.

Физическое поле – форма материи, обеспечивающая передачу воздействия (силового) от одного объекта к другому. В классической модели «физического поля» предполагается, что оно не имеет границ и непрерывно заполняет все пространство.

Известны 4 фундаментальных физических взаимодействия и соответствующие им поля:

- гравитационное;

- электромагнитное;

- сильное;

- слабое.

Электромагнитным называется поле, существующее вокруг «заряженных», т.е. имеющих электрический заряд, объектов. К электромагнитному взаимодействию относятся, в частности, силы упругости и трения, с которыми наиболее часто приходится иметь дело в обыденной практике.

Изложению законов электромагнитного взаимодействия посвящено данное учебное пособие.

ЭЛЕКТРОСТАТИКА

Электрический заряд

Притяжение или отталкивание наэлектризованных тел объясняется существованием электрических зарядов. Электрическим зарядом называется характеристика материального объекта, определяющая его способность создавать электромагнитное поле и взаимодействовать с электромагнитным полем. Заряженные объекты часто коротко называют просто «зарядами».

Основные свойства электрического заряда:

1. Заряд аддитивен, т.е. суммируется : .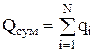

2. Заряд сохраняется: 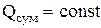, если через границы нет потоков зарядов (электрического тока). Это свойство является фундаментальным физическим законом сохранения электрического заряда. Согласно этому закону любые природные процессы не изменяют алгебраическую сумму зарядов, участвующих в них.

3. Заряд инвариантен: 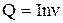. Результат измерения заряда одинаков в любой инерциальной системе отсчета, включая и движущуюся.

4. Заряд дискретен, т.е.:

1) имеется минимальный заряд q_min = e, такой по величине заряд имеет электрон e = 1,6×10^-19 Кл.

Есть определенные теоретические предположения, что существуют частицы, обладающие еще меньшим зарядом и называемые кварками. У них ;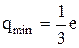

2) любой заряд кратен элементарному:

Q = N×e, где N = ±1, ±2, ±3, …

5. Наличие зарядов двух “сортов” (положительного и отрицательного).

Закон Кулона

Простейшей и наиболее широко применяемой моделью является точечный заряд. Точечный заряд есть материальная точка, имеющая электрический заряд. Эта модель применяется для описания реальных заряженных объектов, размерами которых можно пренебречь в условиях данной задачи.

Сила взаимодействия двух неподвижных точечных зарядов Q₁ и Q₂ называется силой Кулона, а формула, описывающая эту силу – законом Кулона (он был получен экспериментально, и в классической физике рассматривается как постулат):

,

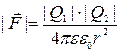где 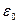– диэлектрическая (электрическая) постоянная, равная 8.85×10^-12 Ф/м; r – расстояние между зарядами;

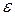–относительная диэлектрическая проницаемость среды, показывающая во сколько раз сила взаимодействия зарядов в среде меньше, чем в вакууме.

Сила направлена по прямой, соединяющей заряды, и для одноименных зарядов является силой отталкивания.

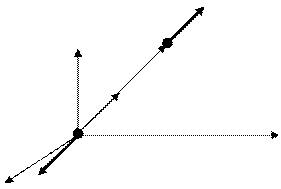
Y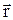

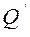
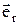
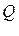X

Z

Рис. 2.1

Удобно использовать 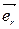единичный вектор, направленный по радиус-вектору. Вспомним, что единичный вектор имеет единичный модуль:

.

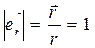Тогда 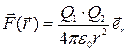- формула силы Кулона взаимодействия между точечными зарядами (закон Кулона в векторном виде) 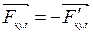(рис.2.1).

Электростатическое поле

Электростатическое взаимодействие передается на расстояние. Это объясняется наличием электростатического поля (ЭСП). Источниками ЭСП являются заряды (заряженные частицы). Обозначим Q – точечный заряд – источник поля. Электростатическое поле воздействует на другие (пробные) заряды. Обозначим соответствующий точечный заряд, как 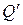. Между ними действует электростатическая сила.

Электростатическим называется поле, создаваемое неподвижными зарядами и действующее на неподвижные заряды. Какая величина может характеризовать электростатическое поле заряда Q? Ясно, что сила, действующая на пробный заряд, зависит от его величины ( ):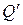

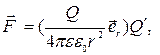
а следовательно не может являться характеристикой электрического поля заряда Q, которое может определяться величиной заряда, создающего поле, расстоянием до точки наблюдения и свойствами среды.

Можно догадаться, что характеристикой электрического поля заряда Q может быть величина, равная отношению силы, действующей на пробный заряд 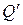, к величине (алгебраической) этого заряда:

.

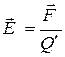Величина 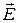, представляет собой силу, действующую на единичный пробный заряд, помещенный в данную точку поля,называетсянапряженностью электрического поля. Напряженность является силовой характеристикой поля, поскольку, если 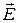известно, легко вычислить силу действующую на любой заряд 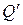, помещенный в поле:

.

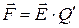Для получения характеристики 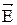, поля точечного заряда, возьмем закон Кулона, как это сделано на рис.3.1 и получим:

.

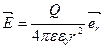Электростатическое поле удовлетворяет принципу суперпозиции: напряженность суммарного поля, создаваемого в данной точке А системой точечных зарядов, равна сумме векторов напряженности полей, созданных каждым точечным зарядом системы.

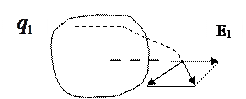А

Е12

Е2

Рис.3.1

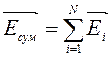Математическая запись принципа суперпозиции для электростатического поля:

Удобным графическим изображением поля являются линии поля или силовые линии.

Линия поля есть геометрическое место точек, в каждой из которых вектор напряженности направлен по касательной к линии поля.

Линии электростатического поля начинаются на положительных зарядах и заканчиваются на отрицательных (или уходят в бесконечность). Расстояние между соседними силовыми линиями или их «густота» расположения в пространстве показывает величину напряженности поля в данной окрестности. Обычно уславливаются проводить силовые линии с такой густотой, чтобы число их, пересекающих площадку площадью 1 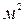, расположенную перпендикулярно линиям поля, равнялось Е.

§ 4. Поток вектора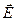

Следующая очень важная дополнительная характеристика электрического поля получила название «поток». Сначала рассмотрим «элементарный поток».

Элементарным потоком вектора напряженности электрического поля через элементарную площадку ds называется скалярное произведение вектора 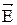на вектор нормали и на величину площадки ds.

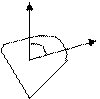
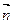
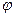
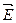
Рис.4.1

.

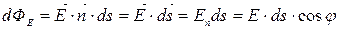Элементарной площадкой называется часть поверхности настолько малая, что по всей этой площадке можно считать, что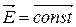(не меняется по величине, не меняется по направлению).

Если проводить силовые линии с определенной ранее густотой, то поток вектора 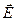через площадку будет численно равен числу силовых линий, пронизывающих данную площадку. При этом силовые линии, пронизывающие площадку в направлении нормали, учитываются со знаком плюс, а против нормали – со знаком минус.

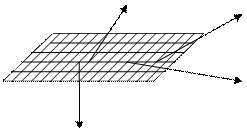
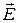
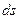
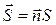
Рис.4.2

Поток через любую поверхность можно вычислить суммированием (интегрированием):

.

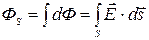Теорема Остроградского - Гаусса и ее применение для расчета электростатических полей

Закон Гаусса - один из фундаментальных законов электродинамики – является одним из фундаментальных законов электродинамики называемых уравнениями Максвелла.

Формула закона:

.

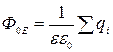Поток вектора напряженности электрического поля через любую замкнутую поверхность (S₀) пропорционален суммарному заряду (åq_i) находящемуся внутри объема V(S₀), ограниченного поверхностью интегрирования S₀.

Запись в расшифрованном виде с использованием локальных характеристик:

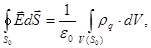
где нули говорят о замкнутости поверхности.

Физический смысл: источником электрического поля являются заряды.

Введено обозначение объемная плотность заряда:

,

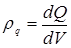где dV – элементарный объем; dQ – элементарный заряд.

Нетрудно доказать теорему Гаусса для точечного заряда. При этом замкнутую поверхность для простоты расчетов можно взять в виде сферы радиуса r, концентрической с зарядом. Это удобно, потому что во всех точках 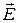направлен по нормали к поверхности и имеет одно и тоже значение:

.

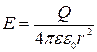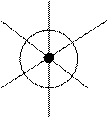
Q,S

Рис.5.1

В этом случае, при вычислении потока постоянное поле можно вынести за знак интеграла, и остается интеграл от элементов поверхности, равный площади выбранной сферической поверхности:

.

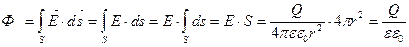Таким образом, справедливость теоремы Гаусса для точечного заряда и сферической поверхности нами доказана. Это доказательство можно обобщить и для любой системы зарядов, и любой замкнутой поверхности.

Теорема Остроградского – Гаусса позволяет определить напряженность электростатического поля любого пространственно-распределенного заряда. В общем случае для этого потребуется использование специальных математических методов решения. Однако для симметричных распределений зарядов удается определить напряженность поля элементарными методами.

В качестве примера определим напряженность поля бесконечной, равномерно заряженной плоскости. Плоскость характеризуется поверхностной плотностью заряда s (заряд, приходящийся на единицу поверхности).

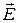
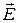
S 1

S А

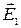
S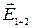

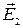
а) в)

Рис.5.2

Схема применения закона Гаусса для вычисления напряженности поля:

1. В случае бесконечной плоскости нетрудно догадаться, что вектор 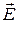должен быть перпендикулярным плоскости. Действительно, на рисунке справа изображено суммарное поле двух точечных зарядов плоскости, расположенных симметрично относительно точки наблюдения А. Как видим, вектор 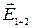перпендикулярен плоскости. В случае бесконечной плоскости для каждого точечного заряда найдется симметричный. Суммируя поля точечных зарядов плоскости симметричными парами, в результате получим поле, перпендикулярное плоскости.

2. Выбираем замкнутую поверхность S₀ в виде прямого цилиндра, пересекающего нашу плоскость в направлении нормали. Такая поверхность удобна для вычисления потока, поскольку через боковую поверхность поток вектора напряженности равен нулю и отличен от нуля лишь через два основания площадью S каждое. Вычисляем (исходя из определения потока):

Ф_0Е = .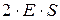

3. Вычисляем суммарный заряд åq_i в объеме, ограниченном поверхностью. На рисунке это заряд заштрихованной части плоскости, площадью S , поэтому:

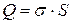
4. Подставляем поток и заряд в закон Остроградского-Гаусса:

.

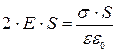5. Из полученного соотношения находим напряженность поля:

.

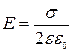Видим, что поле не зависит от расстояния до плоскости, т.е. является однородным.

Потенциал

Напряженность – векторная характеристика электрического поля. Потенции-ал – дополнительная скалярная характеристика поля. Такую характеристику можно вводить только для потенциальных полей, полей, у которых работа сил поля по перемещению объекта по замкнутой траектории равна нулю, а работа по перемещению не зависит от формы пути, по которому произошло перемещение, а зависит только от координат начальной точки 1 и конечной точки 2.

Потенциалом называется скалярная характеристика поля, численно равная работе сил поля по перемещению “пробного” (единичного и положительного) заряда из данной точки, имеющей радиус-вектор , в другую, заранее выбранную точку, имеющую радиус-вектор , в которой потенциал принимается за ноль ( ).

В некоторых случаях .

Элементарная работа сил поля имеет вид (используем сведения, полученные в механике):

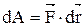= F×dr×cosj.

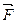
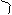
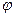
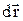
Рис.6.1

Сила в электрическом поле 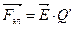, следовательно .

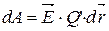И для элементарного приращения потенциала получим:

.

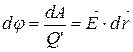Суммируя (интегрируя), получим значение потенциала в точке с координатой 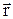, если за начало отсчета принять потенциал точки :

.

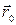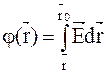Мы получили уравнение связи дополнительной характеристики – потенциала с основной характеристикой – напряженностью.

Задача: получить уравнение обратной связи, т.е. Е через j. Используем выражение для dj 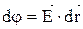и получим:

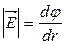
производная по координатам (быстрота изменения в пространстве). Но остается вопрос о направлении поля в пространстве.

Для более точной записи связи потенциала и напряженности используем векторный оператор 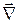, оператор набла, состоящий из трех компонентов:

,

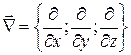где 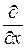; ; 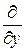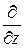– частные производные по координатам (отличаются от обычных производных тем, что вводятся для функции многих переменных и при вычислении производной по одной координате другие координаты надо считать постоянными);

j – скалярная функция трех переменных j(x,y,z). Векторный оператор 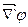для потенциала имеет вид:

,

,

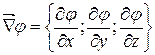Каждая компонента представляет собой составляющие напряженности по трем осям координат 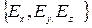. В векторном виде это запишется в виде:

.

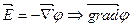Уравнение связи 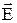и j (grad читается как «градиент»).

По определению потенциал связан с работой по перемещению единичного заряда, следовательно, умножив потенциал на величину пробного заряда, мы получим работу по перемещению этого заряда, т.е. получим потенциальную энергию данного заряда в данной точке электрического поля:

Е_ПОТ. = j× ,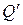

где Е_ПОТ. – потенциальная энергия заряда.

Разность потенциалов

Как использовать потенциал при решении задач?

Удобнее использовать не сам потенциал, а его приращение или изменение, а также «разность потенциалов».

Используя определение приращения любой характеристики и обозначение 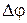– приращение потенциалов, получим:

.
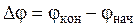