Приведение сосредоточенных масс и моментов инерции масс

Условием динамического приведения масс (моментов инерции) является равенство кинетических энергий приведенной массы m_П (приведенного момента инерции I_П) и всех масс (моментов инерции) действительного механизма.

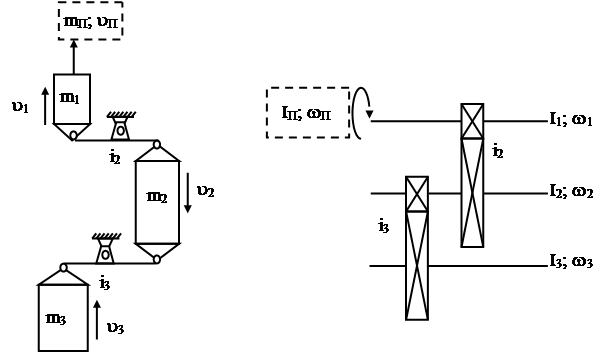
Если массы, движущиеся поступательно (рис. 7а), приводят к точке приложения приведенной массыm_П, движущейся со скоростью u_П, можно записать

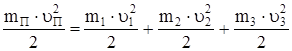, (1)

откуда

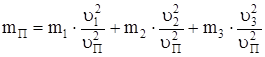. (2)

а) б)

Рис. 7. Условные схемы для приведения:

а) поступательное движение; б) вращательное движение.

Учитывая, что 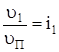, , 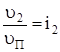, 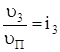для нашей схемы получим

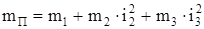. (3)

Аналогично, для вращательного движения масс (рис. 7б)

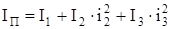. (4)

Если механизм содержит движущиеся поступательно и вращающиеся элементы, массу необходимо выражать через момент инерции или момент инерции через массу.

Например, требуется привести массу груза m, поднимаемого с помощью троса, наматываемого на барабан радиусом R (рис. 8).

Приведенный момент инерции системы

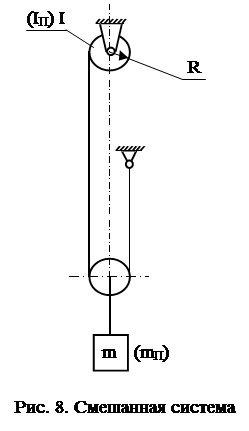
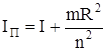, (5)

приведенная масса системы

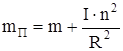, (6)

где n – кратность полиспаста.

Приведение распределенных (рассредоточенных) масс

Для решения задач динамики целесообразно представлять распределенные массы в виде сосредоточенных в заданной точке элемента. При этом должно выполняться сформулированное в п. 1.3 условие как равенство кинетических энергий приведенной (сосредоточенной) массы и всех элементарных масс, распределенных по длине действительного элемента.

Рассмотрим некоторые примеры приведения распределенных масс.

1.4.1. Стержень постоянного сечения (S=const)

Удлинение части стержня длиной x равно

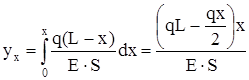, (7)

где q – погонный вес стержня;

E – модуль нормальной упругости;

S – площадь поперечного сечения.

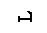
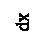
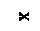
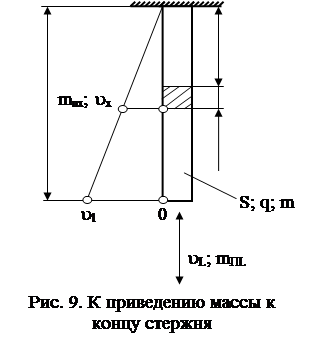При 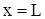получим

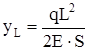. (8)

Поскольку из формулы (8)

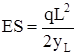, (9)

можем записать:

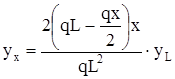. (10)

Скорость перемещения элемента стержня dx равна

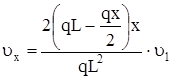. (11)

Кинетическая энергия элемента стержня длиной dx

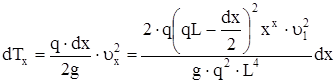. (12)

Кинетическая энергия всего стержня

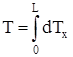. (13)

После интегрирования и преобразований получим

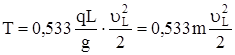. (14)

При приведении распределенной массы стержня m к его концу приведенная кинетическая энергия равна

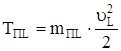. (15)

Таким образом, при условии 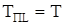получим

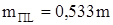. (16)

При приведении распределенной массы стержня m к сечению со скоростью u_x

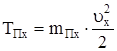. (17)

Из условия 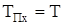будем иметь для любого сечения стержня

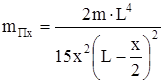. (18)

Консольная балка

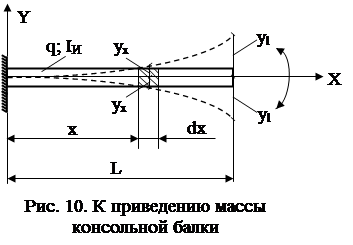При колебаниях балки момент изгиба в сечении X равен

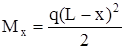, (19)

а уравнение её упругой линии

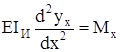. (20)

Интегрируя дважды выражение

,

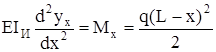получим

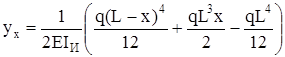. (21)

При x=L имеем

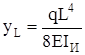. (22)

Тогда формулу (21) можно представить в виде

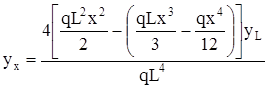. (23)

Кинетическая энергия элемента dx равна

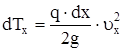, (24)

а всей балки

.

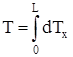Из условия 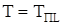получаем

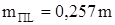, (25)

а для любого сечения балки при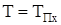

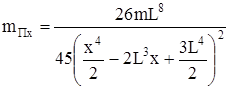. (26)