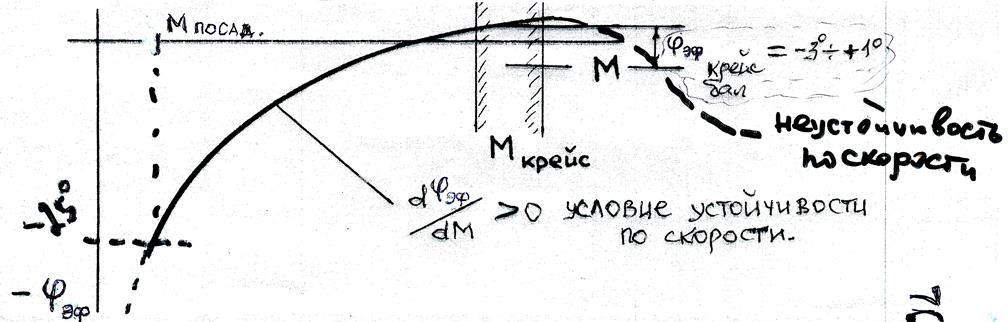
Расчет балансировочной кривой

Можно рассчитать балансировочную кривую (зависимость 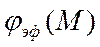), которая относится, как и найденные выше показатели статической устойчивости

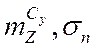, к статическим ХУУ.

Для упрощения примем, что эффективность Г.О. 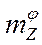соответствует одному из вариантов (с.67).

Расчет производится для ряда фиксированных точек области полета, полет считается установившимся, 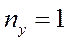, параметры .

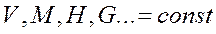Обычно балансировочные кривые строятся для ряда фиксированных значений

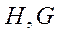, при этом заданы различные величины 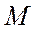для построения кривой .

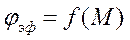Балансировочные кривые относятся к статическим характеристикам устойчивости и управляемости. Для расчета балансировочной кривой используются упрощенные соотношения для 4-5-и значений скорости 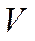, высоты 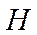, массы .

10. Расчет динамических характеристик устойчивости и управляемости

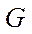Выше (стр.55) отмечены уравнения для решения коротко-периодического движения.

Определения:

Статическая устойчивость – способность самолета без вмешательства летчика создавать моменты, направленные на возвращение самолета к исходному равновесному состоянию после прекращения действия возмущения.

Динамическая устойчивость – соответствие переходного процесса заданным нормам.

Управляемость самолета – способность изменять положение в пространстве в ответ на усилия и перемещения на рычагах управления, создаваемые летчиком (способность самолета «ходить за ручкой»).

Самолет должен быть устойчивым относительно всех трех осей. Ниже рассматривается только продольная устойчивость.

10.1. Методы расчета динамических характеристик устойчивости и управляемости

Оценка характеристик устойчивости и управляемости производится в выбранных точках области полета, для которых значения высоты 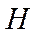, скорости 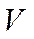, числа 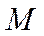, режима работы двигателя 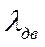, полетного веса 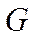принимаются постоянными величинами.

Расчеты включают:

- расчет основных показателей переходного процесса по углу атаки 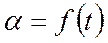в ответ на возмущающее воздействие;

- оценку улучшения характеристик устойчивости и управляемости с помощью демпфера тангажа. Рассматриваются такие показатели переходного процесса 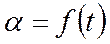, как время срабатывания 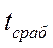, относительный заброс 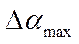, время затухания 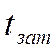(см. рис. ).

Исходными данными для расчетов являются величины момента инерции 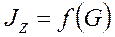, а также , , , , , , , , , , .

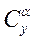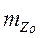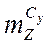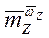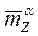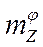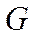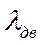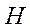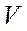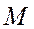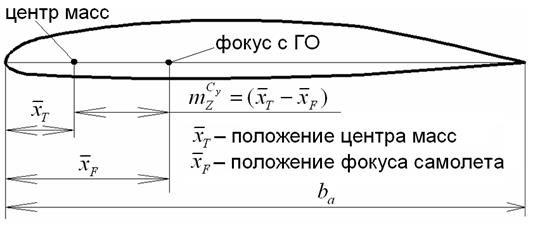
Окончательная летная оценка дается в процессе летных испытаний, но предварительная оценка может быть получена путем решения приведенных выше уравнений.

Допущение: возмущения, действующие на самолет, считаются малыми, например, возмущение угла атаки при вертикальном порыве ветра:

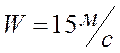- скорость нормированного порыва ветра,

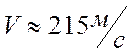- скорость крейсерского полета.

.

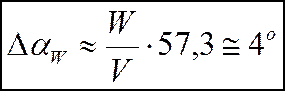Когда возмущения относительно опорной траектории малы, можно считать их линейной функцией.

Например, участок кривой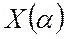

при малом 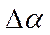можно считать прямой линией,

т.е. 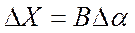, в то время как вся функция -

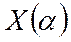нелинейная.

Представление исходных уравнений движения в линейном виде называется линеаризацией. Полученная система линейных дифференциальных уравнений может быть решена аналитически.

Для линеаризации используется метод разложения в ряд Тейлора с оставлением только слагаемых 1^й степени:

.

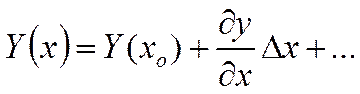Рассмотрим подробно линеаризацию уравнения 1:

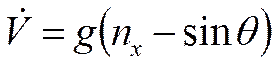– исходное нелинейное уравнение.

,

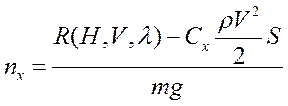линейное уравнение в приращениях:

,

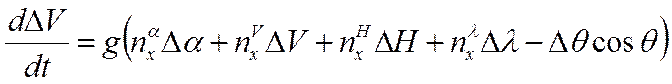
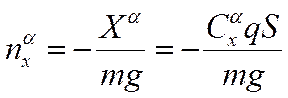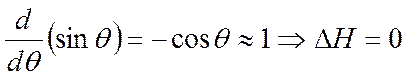, и т.д.

.

Тем же методом превращаются в линейные остальные уравнения. Рассмотрим подробнее правую часть уравнения моментов:

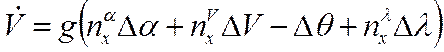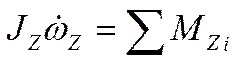, где

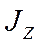– момент инерции самолета,

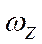– угловая скорость относительно оси ,

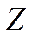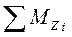– сумма моментов сил, приложенных к различным частям самолета.

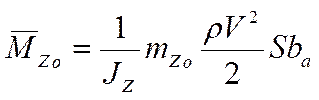– момент, обусловленный асимметрией самолета,

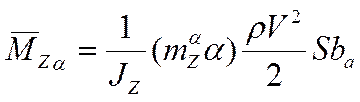– момент, возникающий на счет угла атаки,

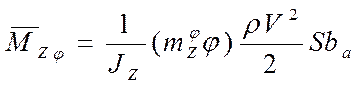– момент от руля высоты,

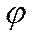– угол отклонения Р.В.( ),

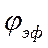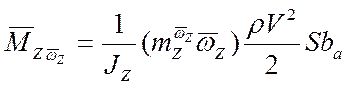– момент собственного демпфирования.

75А

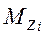Эти слагаемые обозначим , тогда в приращениях будем иметь линейное уравнение:

.

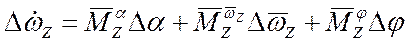Отметим относительно последнего уравнения:

1. Поскольку мы рассматриваем для упрощения только продольное коротко-периодическое движение, (т.е. 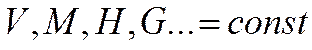), то в формулы для коэффициентов не входят производные по , , , .

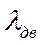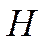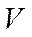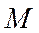2. По этой же причине коэффициенты в правой части уравнения 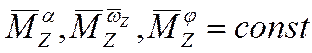, поэтому это – линейное дифференциальное уравнение 1^го порядка с постоянными коэффициентами, которое решается аналитически.

3. Вместо угловой скорости 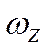применяется параметр 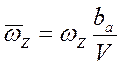, эквивалентный 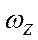для условия .

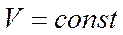4. Исключается слагаемое 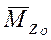, т.к. является константой и не оказывает влияния на устойчивость.

Уравнения для коротко-периодического движения:

1.)

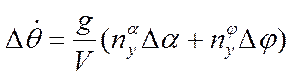
2.)

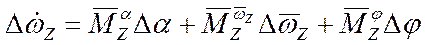
3.)

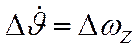
4.)

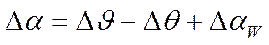
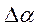Имеем 4 уравнения и 6 неизвестных, обычно задаются два возмущения и .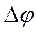

Для определения математического условия устойчивости преобразуем систему из 4-х уравнений в одно уравнение положив, что 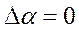, , 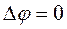т.е. получим однородное линейное уравнение для расчета собственного движения самолета (как правило – собственных колебаний):

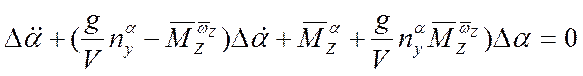(***), пусть:

,

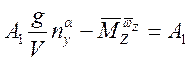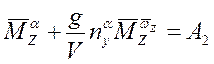, тогда

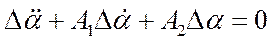(*), либо

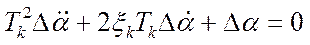(**), где 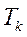– постоянная времени переходного процесса, равная обратной величине круговой частоты недемпфируемых колебаний самолета , .

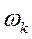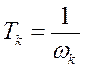Оба уравнения абсолютно идентичны и коэффициенты 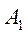и 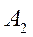могут быть выражены через коэффициенты .

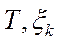В большинстве случаев решения уравнений (*) и (**) описывают затухающие колебания, реже – апериодическое движение.

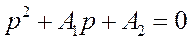– характеристический многочлен,

корни которого: ,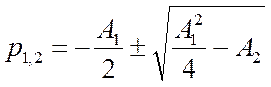

если 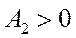– корни комплексные, движение колебательное, затухающее,

если 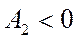– корни вещественные, движение апериодическое.

Поскольку коэффициенты 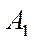и 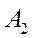– постоянны, т.к. они вычисляются согласно формулам в уравнении (***), куда входят параметры установившегося опорного движения, то вычислив 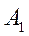и 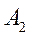можно сделать качественное заключение о типе переходного процесса и его устойчивости. Количественные оценки получаются только из рассмотрения решения переходной функции по времени. Для получения такого решения требуется большое число исходных данных, поэтому ниже рассмотрен конкретный пример расчета коротко-периодического движения самолета типа Ту-154 – изменение угла атаки 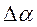в ответ на возмущающее воздействие скачкообразного порыва ветра. Задавая 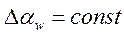, уравнение будет неоднородным, однако его решение будет совпадать с решением однородного уравнения.

Качество переходного процесса определяет динамические характеристики устойчивости и управляемости в коротко-периодическом движении самолета, который рассматривается как колебательное звено 2^го порядка. Дифференциальное уравнение колебательного движения имеет вид (по теории см. Смирнов В.И. Курс высшей математики Т.2):

.

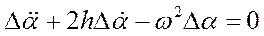Общий интеграл:

,

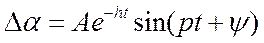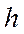– коэффициент затухания;

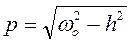– частота колебаний;

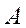– амплитуда колебаний;

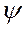– начальная фаза колебаний.

Удобнее переходную функцию 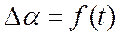выражать в относительных величинах

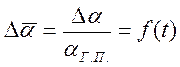, где

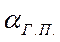– угол атаки в установившемся горизонтальном полете,

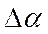– отклонение угла атаки от .

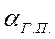Зависимость 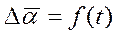имеет вид (без вывода):

,

, .

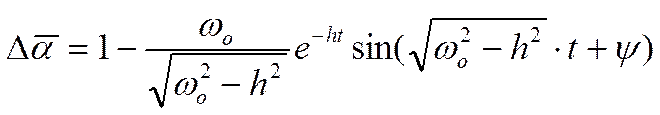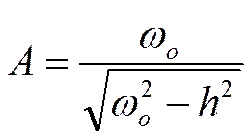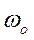Выражения для и 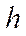записываются через аэродинамические коэффициенты самолета и момент инерции 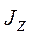и следуют из линеаризованных уравнений коротко-периодического движения самолета (см. (*),(**),(***)).

,

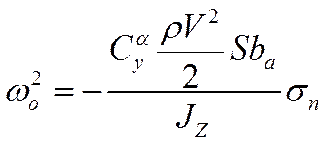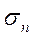– запас устойчивости с учетом аэродинамического демпфирования:

,

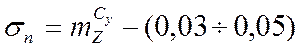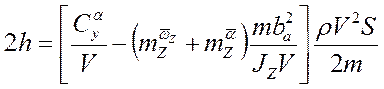, развернутое выражение для коэффициента .

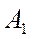Значения 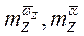безразмерные, 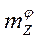, 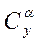имеют размерность 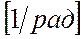, размерность – , , , , .

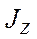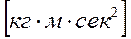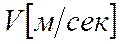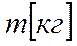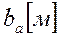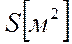Характерные параметры переходного процесса (рис. ):

1. Постоянная времени:

;

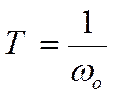2.

Период колебаний:

;

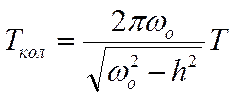3. Относительный заброс (I-й экстремум):

;

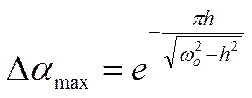4. Время срабатывания:

;

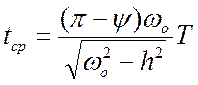5. Время затухания:

.
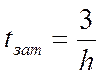