Коэффициент магнитной проводимости пазового рассеяния.

Предположим, что в пазу с высотой h_п расположено N_п проводни­ков однослойной обмотки (рис. 5.2). Примем следующие допуще­ния: проводники с током распределены равномерно по всей площа­ди поперечного сечения паза, плотность тока в каждой точке сечения паза постоянна, магнитная проницаемость стали магнито­провода равна бесконечности, магнитные линии потока рассеяния в пазу прямолинейны и направлены нормально к оси паза.

Все рас­смотрение будем проводить относительно единицы условной длины l'δ. Для того чтобы учесть потокосцепление потока рассеяния с проводниками об­мотки, выделим в пазу на высоте hx от дна паза элемент высотой dx, представляющий собой трубку потока рассея­ния паза. Поток этого элемента на единицу длины обозначим dФσх. Создаваемое им потокосцепление с проводниками обмотки Nx, расположен­ными в пазу ниже выделенного элемента, равно: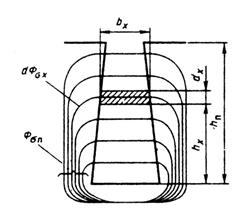

Рис. 5.2. К расчету коэффициен­та магнитной проводимости по­тока пазового рассеяния

dѰ_х = dФ_σх N_х (5.9)

При принятом допущении об отсутствии насыщения стали мож­но записать

dФ_σх = μ₀ F_x dΛ_x, (5.10)

где dΛ_x, = dx/ b_x — магнитная проводимость выделенного элемента паза; b_х — ширина паза на высоте h_x.

Учитывая, что F_x = N_xI, где I — ток в одном проводнике, из (5.9) и (5.10) получаем

dѰ_х = μ₀I N²_x .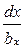

Потокосцепление всего потока рассеяния паза со всеми провод­никами, расположенными в данном пазу, равно:

Ψ_п = μ₀I 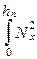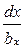(5.11)

откуда индуктивное сопротивление проводников одного паза на еди­ницу длины

х'_σп = ωL_п = ω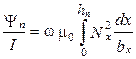

или (5.12)

х'_σп = 2π f μ₀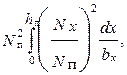

где N_п — полное число проводников в пазу.

Интеграл в правой части выражения (5.12) определяет коэф­фициент магнитной проводимости потока пазового рассеяния с учетом потокосцепления с проводниками паза. Его обозначают λ_пψ

λ_пψ= 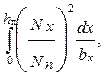(5.1З)

Так как при расчете индуктивного сопротивления рассеяния учет потокосцепления обязателен, индекс ψ в обозначении обычно опускают, тогда

х'_σп = 2π f μ_{0 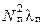.} (5.14)

Выразив N_п через число витков фазы (при условии, что обмотка фазы расположена в Z/m пазах), получим выражение для индуктив­ного сопротивления пазового рассеяния всей фазы с учетом услов­ной длины поля рассеяния:

х_σп = 4π f μ₀ 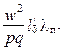(5.15)

Расчетные формулы для определения λ_п получают из (5.13) с учетом конфигурации пазов и типа обмотки.

В частном случае коэффициент магнитной проводимости прямо­угольного паза полностью занятого проводниками однослойной об­мотки

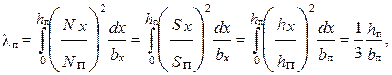(5.16)

так как в прямоугольном пазу ширина b_x = b_п постоянна и не зави­сит от высоты, а при принятом допущении о равномерности рас­пределения проводников по площади сечения паза справедливо равенство

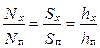
где S_п — площадь поперечного сечения паза, занятая проводниками с током, а S_x — часть площади сечения паза, ограниченная высотой h_x. В более сложных случаях, например, когда проводники с током занимают не весь паз и конфигурация паза отлична от прямоуголь­ной, коэффициент проводимости пазового рассеяния

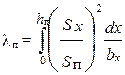(5.17)

где Sп и Sx — площади поперечного сечения паза, за­нятые проводниками обмотки. Интегрирование проводят по частям паза, при­чем паз делят по высоте таким образом, чтобы в пределах каждой части ширина паза могла быть вы­ражена аналитически в зависимости от высоты, а плотность тока в каждой точке ее сечения была оди­наковой. Например, для прямоугольного паза со свободной от обмотки верхней — клиновой частью (рис. 5.3) таких участков интегрирования будет три: нижняя часть паза, занятая изоляцией высотой h0, часть паза с однослойной обмоткой высотой h1 и клиновая часть с высотой h2. Коэффициент магнитной проводимости всего паза равен: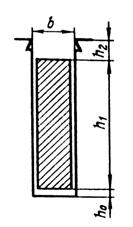

Рис. 5.3. К расчету λп прямоугольного паза с одно­слойной обмоткой

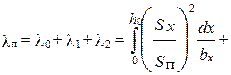
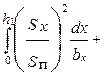
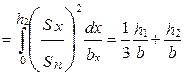(5.18)

В двухслойных обмотках с укороченным шагом в части пазов размещены стороны катушек, принадлежащих разным фазам, по­этому токи в них сдвинуты во времени. Это влияние на потокосцепление пазового рассеяния в расчетных формулах учитывается коэффициентами k_β и k'_β, зависящими от укорочения шага об­мотки.

Чтобы не производить интегрирование при каждом расчете для наиболее часто встречавшихся конфигураций пазов, формулы рас­чета пазового рассеяния приводятся в виде справочных таблиц в со­ответствующих главах.

Коэффициент магнитной проводимости лобового рассеяния принципиально можно найти методом, аналогичным, описанному выше, однако индуктивное сопротивление лобовых частей обмоток определяется не только индуктивностью каждой из катушек, но и взаимоиндуктивными связями лобовых частей всех катушек обмотки. Это значительно усложняет расчет, так как поле рассеяния в зоне расположения лобовых частей имеет более сложный характер, чем в пазах. Криволинейность проводников в лобовых частях, разнообразные в различных машинах конфигурации поверхностей фер­ромагнитных деталей, окружающих лобовые части, и сложный характер индуктивных связей усложняют аналитический расчет λ_л и требуют для его выполнения ряда упрощающих допущений. В практических расчетах коэффициент магнитной индукции лобового рас­сеяния обмотки λ_л определяют по относительно простым эмпириче­ским формулам, полученным на основании многочисленных экспериментальных исследований, проведенных для различных ти­пов и конструкций обмоток. При вычислении значение λ_л также от­носят к единице условной длины l'_δ.

Коэффициент магнитной проводимости дифференциального рассеяния. Полем дифференциального рассеяния называют всю совокупность полей различных гармоник в воздушном зазоре, не участвующих в создании электромагнитного момента. Потокосцепление этих полей с витками обмотки определенным образом увеличивает ее индуктивное сопротивление, что учитывается ко­эффициентом магнитной проводимости дифференциального рас­сеяния λ_д. Его значение зависит от размерных соотношений воз­душного зазора, числа пазов на полюс и фазу q, размеров шлица, зубцовых делений, степени демпфирования полей высших гармо­ник токами в проводниках, расположенных на противоположной от рассматриваемой обмотки стороне воздушного зазора, и от ряда других факторов.

Индуктивное сопротивление рассеяния обмотки определяют по формуле, аналогичной (5.15), в которую вместо λ_п подставляют сум­му коэффициентов магнитных проводимостей пазового, лобового и дифференциального рассеяний:

х_σ = 4π f μ₀ 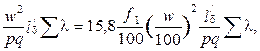(5.19)

где .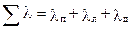

В асинхронных машинах индуктивное сопротивление фазы об­мотки статора обозначают x₁, а обмотки ротора x₂. В синхронных машинах индуктивное сопротивление рассеяния обмотки статора обозначают x_σ1. В машинах постоянного тока индуктивное сопротивление обмотки якоря непосредственно не рассчитывают, однако коэффициенты магнитной проводимости рассеяния определяют для расчета реактивной ЭДС секций обмотки.

Индуктивные и активные сопротивления обмоток в уравнениях напряжений являются коэффициентами перед токами. Эти парамет­ры входят как в дифференциальные уравнения, описывающие пере­ходные и установившиеся режимы, так и в комплексные уравнения, описывающие только установившиеся процессы [6].

Расчетные формулы для определения коэффициентов магнитных проводимостей пазового, лобового и дифференциального рассеяний непосредственно связаны с формой и размерами пазов, типом и кон­струкцией обмоток и размерными соотношениями зубцовой зоны. Эти факторы для разных типов машин различны. Расчет коэффици­ентов магнитных проводимостей рассеяния асинхронных и синхрон­ных машин, а также машин постоянного тока приводится в соответ­ствующих главах.

МОМЕНТ ИНЕРЦИИ

Момент инерции характеризует динамические свойства машины. Он входит в уравнение движения

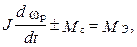(5.20)

где J — момент инерции; ω_р — угловая скорость ротора; М_с — мо­мент сопротивления; М_э — электромагнитный момент.

Момент инерции вращающегося тела равен сумме произведений масс всех его точек на квадраты их расстояний от оси вращения. Значение момента инерции тела относительно оси OZ может быть получено из интеграла

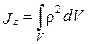, (5.21)

где ρ — расстояние до оси вращения 0Z; dV — элемент объема.

Для тел, имеющих простую геометрическую форму (цилиндр, диск и т. п.), значения моментов инерции приводятся в справочниках. Например, момент инерции полого цилиндра массой m, длиной l, внешним радиусом R₁ и внутренним R₂ равен:

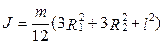. (5.22)

Момент инерции сплошного цилиндра (R₁ = R; R₂=0)

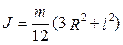(5.23)

Как видно, при одном и том же объеме момент инерции тела с меньшим радиусом будет меньше, чем при большом радиусе.

Момент инерции является мерой инертности тела, поэтому дви­гатели с малым моментом инерции разгоняются с большими ускоре­ниями и быстро достигают установившейся частоты вращения. Для эксплуатации в режимах с частыми пусками стремятся выполнить двигатели с малыми моментами инерции, для чего уменьшают диа­метры роторов при соответствующем увеличении длин их сердечни­ков.

В приводах с ударной или пульсирующей нагрузкой (поршневые компрессоры) целесообразно применять двигатели, имеющие боль­шой момент инерции, т. е. с относительно большим диаметром ро­тора и малой длиной. При постоянной частоте вращения кинетиче­ская энергия вращающегося тела пропорциональна его моменту инерции, поэтому двигатели с большим моментом инерции облада­ют большой кинетической энергией, за счет которой преодолевают­ся толчки нагрузки.

Ввиду сложности конфигурации роторов электрических машин и наличия в них элементов с различной удельной массой (сталь сер­дечников, обмотка, изоляция, детали крепления) для расчета момен­та инерции ротор делят на несколько частей, имеющих сравнитель­но простую конфигурацию, и для каждой из них определяют J, руководствуясь формулами специальных методик.

При расчете динамических характеристик двигателя вместе с приводом учитывают моменты инерции механизмов, соединенных с валом двигателя, значения которых приводят к частоте вращения ротора. Общий приведенный момент инерции определяют по фор­муле

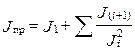(5.24)

где J₁ — момент инерции ротора двигателя; J_(i+1) — моменты инерции механизмов, соединенных с валом ротора; j_i — передаточное отноше­ние i-й передачи, равное отношению частот вращения данного меха­низма и ротора двигателя.