Признак сходимости монотонной последовательности
Рассмотрим числовую последовательность {хn}: х1, х2,…, хn,… (1)
Последовательность (1) называется возрастающей (неубывающей), если "nÎN, xn+1³xn. Если имеет место xn+1>xn, то (1) – строго возрастающая последовательность.
Последовательность (1) называется убывающей (невозрастающей), если "nÎN, xn+1£xn. В случае xn+1<xn, последовательность (1) строго убывает.
Последовательность (1) ограничена сверху [снизу], если ($bÎR):("nÎN) ®xn£b [xn³b].
Аналогично точным граням числовых множеств можно ввести:
;
.
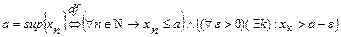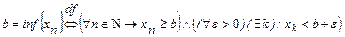Теорема(Вейерштрасс). Всякая монотонная ограниченная последовательность имеет предел:
;
.
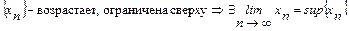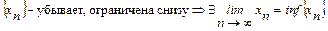gПусть последовательность {xn} ограничена сверху. По теореме о точных гранях существует число a=sup{xn}: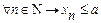 
, (2) ("e>0)($k): xk>a – e. (3) По условию {xn} – возрастающая последовательность, поэтому "n>k ® xk £ xn. (4)
Из условия (2) имеем: "nÎN ® xn£a<a+e. (5)
Неравенство (5) подавно выполнено для n>k. Из условий (3), (4), (5) следует, что
,
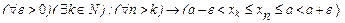т.е.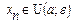 
и 
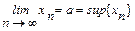.n