Частотные свойства цепей переменного тока

Частотной характеристикой называется зависимость параметров цепи от частоты (например ). Активное сопротивление устройств от частоты не зависит. Зависимость индуктивного и емкостного сопротивлений от частоты определяется формулами:

и . Графики зависимости реактивных сопротивлений от частоты представлены на рис. 2.15.

Рис. 2.15 – Графики зависимости реактивных сопротивлений

от частоты

Рассмотрим цепь из последовательно соединенных R, L, C элементов (рис. 2.15). На участке цепи с последовательно соединенными R, L, C элементами найдется такая частота (резонансная) при которой сопротивления 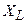и окажутся равными_.

При этом, и полное сопротивление Z окажется чисто активным и равным R. Такой режим называется режимом резонанса напряжений. Резонансная частота: .

Пример: Дана цепь из последовательно соединенных R, L, C элементов . Определить токи , напряжения, мощности и и изучить их зависимости от частоты.

Рис. 2.16

1) Согласно второго закона Кирхгофа:

ЭДС источника отсутствует, Е = 0, контур К обходим по часовой стрелке

Так как цепь последовательная, то ток один и тот же, поэтому:

.

Рассчитаем ток в цепи: .

Если , то то есть сопротивление цепи становиться чисто омическим, при этом ток в цепи максимальный , а падения напряжений на емкости и индуктивности будут по величине одинаковыми: , но фазы напряжений , , сдвинуты на 180 градусов, то есть направления векторов , , противоположны. Или говорят, что напряжения на индуктивности и на емкости находятся в противофазе.

Сдвиг фаз между током и входным напряжением:

,

так как при резонансе .

Вывод:

1) При резонансе напряжений величина напряжения на конденсаторе равна величине напряжения на индуктивности.

2) Напряжения на всех элементах схемы максимальны:

.

3) При резонансе напряжений сдвиг фаз между входным напряжением и током в цепи равен нулю.

4) Резонансная частота рассчитывается из условия равенства величин реактивных сопротивлений: или .

5) Суммарное напряжение на реактивных элементах при резонансе равно нулю. Между точками би г напряжение равно нулю. Вольтметр, включенный между точками би г покажет 0 (ноль) вольт.

6) Падение напряжения на сопротивлении равно входному напряжению .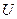

7) Полная мощность в цепи будет чисто активной. , так как .

Активная мощность в цепи будет максимальной: .

8) Реактивные мощности на каждом из реактивных элементов так же максимальны и равны соответственно:

;

.

Суммарная реактивная мощность при резонансе равна нулю, .

Рис. 2.17 – Векторная диаграмма токов и напряжений при резонансе при последовательномсоединении R, L, C элементов

Вероятные вопросы при тестировании по теме 2.7:

1.Резонансная частота в цепи при последовательном соединении R,L,C элементов равна :

(а)

(б)

(в)

(г)

(Ответ (в)

1. При резонансе в цепи при последовательном соединении R,L,C элементов максимальный ток равен:

(а)

(б)

(в)

(г)

(Ответ (б)

3.При резонансе коэффициент мощности cos φ равен:

(а)- 0;

(б)- 0,5;

(в)- 0,865;

(г)- 1.0

(Ответ (г)

4.При резонансе напряжение на конденсаторе U_C сдвинуто относительно напряжения на индуктивности U_L на угол:

(а)- 0 ˚;

(б)- минус180˚;

(в)- плюс90˚;

(г)- плюс 45˚

(Ответ(б)

4.При резонансе потребляемая мощность :

(а)- чисто активная;

(б)- чисто реактивная ;

(в)- ;

(г )-

(Ответ(а)

3

Трехфазные цепи. Основные понятия. Элементы трехфазных цепей

Определения

Трехфазной цепью называют электрическую цепь образованной из источника трехфазной ЭДС и трехфазного приемника.

Трехфазный генератор, принцип действия и устройство.

Трехфазный генератор состоит из трех однофазных генераторов расположенных в одном корпусе. Оси обмоток каждого из генераторов геометрически смещены относительно друг друга на или на 1/3 оборота.

На рис. 3.1 (а) схематично показано устройство трех фазного генератора.

Рис. 3.1 –Трехфазный генератор

а – схематичное изображение устройства генератора, b – схема соединения обмоток генератора по схеме звезда без нейтрального провода, c – схема замещения (идеального) трехфазного генератора

На статоре расположены 3 пары обмоток AX, BY, CZ. Ротор (электромагнит или постоянный магнит) при равномерном вращении возбуждает в каждой из обмоток (фазах) переменную (синусоидальную) ЭДС (согласно закону электромагнитной индукции). Так как оси обмоток геометрически смещены на , (1/3 оборота), то время наступления максимума ЭДС в каждой обмотке будет сдвинуто на 1/3 периода вращения ротора. Говорят, что фазы ЭДС в каждой из обмоток сдвинуты на 120⁰.

Закон изменения и соответствующие графики мгновенных значений фазных ЭДС на клеммах генераторов можно представить в виде уравнений и графиков на рис. 3.2:

Рис. 3.2 – Эпюры мгновенных значений фазных напряжений трех фазного генератора

Большими буквами А, В, С и X, Y, Z обозначают начала и концы обмоток генератора. Концы и начала сопротивлений нагрузки обозначают малыми буквами a, b, си x, y, z соответственно.

Обмотки генератора могут соединяться по схеме звезда (с выводом и без вывода нейтрального провода) или по схеме треугольник. Внутренне сопротивление генератора мало и в дальнейшем будем считать его равным нулю ( ).

а б

Рис. 3.3 – Схемы замещения и условные обозначение схем соединения трех фазных обмоток генератора по схеме звезда (а) и по схеме треугольник (б)

На электрических схемах они обозначаются следующим образом:

Рис. 3.4 – Условные обозначения схем соединений обмоток генератора: звезда, звезда с нейтральным проводом, треугольник

Комплексные ЭДС генератора представляются в виде:

Напряжение на клеммах генератора , , (при ) равно соответственно ЭДС генератора , , .

Для симметричного генератора выполняется соотношение:

.

Соединение генератора и приемника по схеме звезда – звезда

Соединение генератора и приемника по схеме звезда –звезда приведены на рис. 3.5.

Рис. 3.5 – Соединение приемника и генератора звездой

Определения и обозначения

– фазные напряжения генератора;

При соединении звездой фазные напряжения генератора обозначают: ;

– фазное напряжение нагрузки;

– линейные напряжения генератора;

– линейные напряжения нагрузки;

¾ – напряжение смещения нейтрали;

– фазный ток нагрузки фазы А;

– линейный ток в проводе Аа;

Обычно вместо , , пишут , ( ) или .

Если все фазные напряжения равны, то генератор называется симметричным.

Приемник соединен по схеме звезда аналогичным образом. Точка соединения концов нагрузок фаз приемника обозначают буквой n.

Если нейтрального провода нет, то при неравномерной нагрузке ( ) между точками и 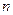появляется напряжение . называют напряжением смещения нейтрали.

Для симметричного приемника:

;

. (3.5д)

Для несимметричного приемника с нейтральным проводом в нейтральном проводе появляется ток:

.

Для симметричного генератора линейные и фазные напряжения связаны соотношением:

.

Соединение генератора и приемника по схеме звезда –треугольник

Соединение генератора звездой и приемника треугольником представлено на рис. 3.6.

Рис. 3.6 – Соединение генератора звездой и приемника треугольником

По первому закона Кирхгофа для приемника:

.

Линейные напряжения генератора равны напряжениям на фазных нагрузках приемника:

; ; . (3.7в)

Вектор линейного напряжения генератора равен разности векторов фазных напряжений генераторов:

; ; .