Тема: Дослідження функцій та побудова їх графіків

Дослідження функцій і побудову їх графіків можна проводити за такою схемою:

1) Область визначення функції.

2) Точки розриву графіка функції.

3) Точки перетину графіка функції з координатними осями.

4) Дослідження функції на парність.

5) Дослідження функції на монотонність та екстремум.

6) Дослідження функції на напрям угнутості та точки перегину.

7) Асимптоти графіка функції.

8) Графік функції.

Приклад:Дослідити функцію та побудувати її графік:

1.

2. – точки розриву другого роду. Оскільки

3.

4. і, отже, дана функція є непарною, а її графік симетричний відносно початку координат.

5. Далі досліджуємо похідну даної функції: .

Похідна дорівнює нулю при

При значення похідної позитивні, при - негативні.

Таким чином, на множині функція зростає, а на множині - спадає.

Оскільки при переході через похідна міняє знак із плюса на мінус, то максимум функції.

Оскільки при переході через похідна міняє знак з мінуса на плюс, то мінімум функції.

Оскільки при переході через x = 0 похідна не міняє знака, то y(0) = 0 не є екстремумом функції.

Таким чином, P₁- точка максимуму, а P₂ - точка мінімуму графіка функції.

6. Тепер досліджуємо другу похідну:

При значення другої похідної негативні, при позитивні, y'' = 0 при x = 0.

Таким чином, на множині графік функції опуклий, а на множині - вгнутий, P₃(0; 0) - точка перегину.

7. а) Оскільки - точки розриву другого роду, то рівняння визначають вертикальні асимптоти..

б) Знайдемо похилу асимптоту у вигляді рівняння , де

Таким чином, y = x - похила асимптота.

8. На підставі проведеного дослідження функції будуємо її графік (рис. 4).

Рис. 4

Завдання для роботи в аудиторії:

Дослідити функцію та побудувати її графік:

1) у = - х³ + х² + 3х – 6;

2) у = ;

3) у = ;

4) у = 8х²

5) у = х .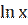

Домашнє завдання:

Дослідити функцію та побудувати її графік:

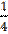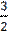1) у = х³ - х² + 2;

2) у = ;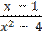

3) у = ;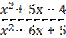

4) у = 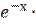х²;

5) у = 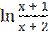.