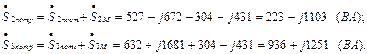Метод узловых потенциалов

Пронумеруем узлы схемы изображенной на рисунке 7.3

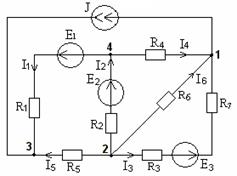
Рисунок 7.3

Система уравнений по методу узловых потенциалов содержит n уравнений:

n = у–1 = 4–1 = 3,

где у – количество узлов схемы.

Примем потенциал четвертого узла равным нулю j₄=0. Запишем систему уравнений:

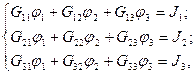(7.3)

где 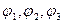– потенциалы первого, второго и третьего узлов;

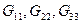– собственные проводимости узлов. Собственная проводимость всегда положительна и равна сумме проводимостей ветвей, присоединенных к данному узлу.

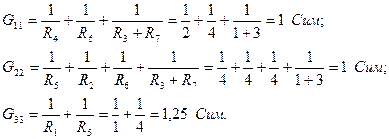
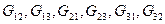– общие проводимости. Общая проводимость всегда отрицательна и равна сумме проводимостей ветвей, соединяющих два данных узла.

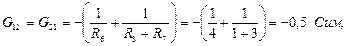
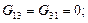
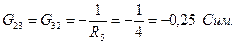
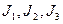– узловые токи. Узловые токи равны алгебраической сумме токов источников тока и произведений ЭДС на соответствующую проводимость ветви, присоединенных к рассматриваемому узлу. Если источник направлен к узлу, то слагаемое входит с положительным знаком, и с отрицательным знаком, если источник направлен от узла.

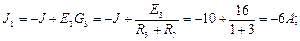
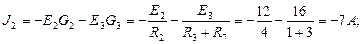
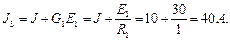
Найденные параметры узлов подставляем в систему уравнений:

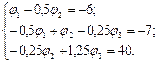
Решив данную систему уравнений, получим значения потенциалов узлов:

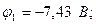
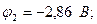
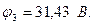
Токи ветвей определяем на основании обобщенного закона Ома: ,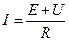

где напряжение U определяется разностью потенциалов узлов, к которым присоединена данная ветвь.

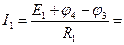
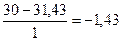
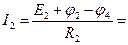
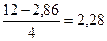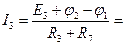
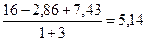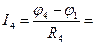
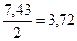А; А;

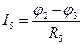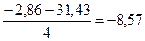А;

А;

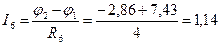= А;

А.

7.1.4 Баланс мощностей.

Определяем вырабатываемую мощность:

Р_выр=E₁I₁+E₂I₂+E₃I₃ +JU_J , (7.4)

где U_J - напряжение на зажимах источника тока.

Напряжение U_J (см. рис. 7.3) можно определить, применив второй закон Кирхгофа:

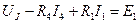; (7.5)

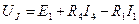
=30+ 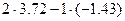=38.87 В.

Если известны потенциалы узлов, напряжение можно определить как разность потенциалов:

U_J= 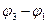=31,43+7,43=38,86 В;

Р_выр.= 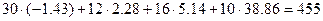Вт.

Определим потребляемую мощность:

Р_потр.=R₁I₁²+R₂I₂²+(R₃+R₇)I₃²+R₄I₄²+R₅I₅²+R₆I₆²=

=

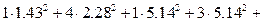
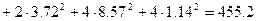Вт.

Р_выр.= Р_потр; 455,3 Вт 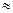455,2 Вт.

Баланс мощностей выполняется. Погрешность расчетов:

D= 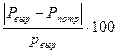%= 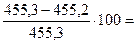0,02 %.

Примечание: Погрешность не должна превышать 5%.

7.1.5 Метод эквивалентного генератора.

Определим ток во второй ветви. Согласно теореме об эквивалентном генераторе, как видно из рисунка 7.4, ток определяем по формуле (7.6): :

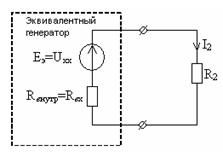
Рисунок 7.4

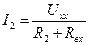, (7.6)

где U_xx-напряжение холостого хода;

R_вх- входное сопротивление.

Определим напряжение холостого хода. При размыкании ветви с резистором R₂ схема имеет вид, показанный на рисунке 7.5. Это активный двухполюсник, который заменяют эквивалентным генератором с параметрами: Е_э= U_xx; R =R_вх.

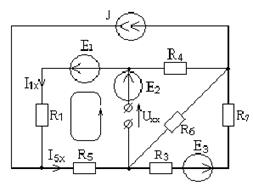
Рисунок 7.5

По второму закону Кирхгофа запишем уравнение для контура, содержащего напряжение U_xx (см. рис.7.5):

U_xx+R₁I_1x+R₅I_5x=E₂+E₁. (7.7)

Отсюда определяем напряжение холостого хода:

U_xx=Е₂+Е₁- R₁I_1x- R₅I_5x . (7.8)

Токи активного двухполюсника I_1x и I_5x находим, применив метод наложения , согласно которому ток в любой ветви линейной электрической цепи равен алгебраической сумме токов , вызываемых в этой ветви каждым источником энергии в отдельности. В процессе определения тока , вызываемого в данной ветви одним источником энергии, остальные источники энергии исключаются из схемы , но остаются их внутренние сопротивления. При исключении идеальных источников ЭДС их зажимы закорачивают (внутреннее сопротивление равно нулю) , а при исключении идеальных источников тока соответствующие ветви размыкают (внутреннее сопротивление равно бесконечности).

Согласно методу наложения схему (см. рис.7.5) разбиваем на три схемы , в каждой из которых работает один источник. При этом учтем, что источник Е₂ не может создавать токов, так как он включен в разомкнутую ветвь.

Определяем токи I_1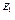x и I_5x 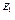, обусловленные действием источника ЭДС Е₁. Схема представлена на рисунке 7.6.

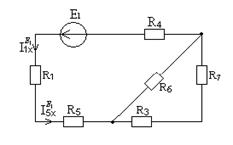
Рисунок 7.6

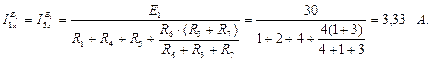
Определяем ток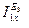и и 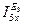, обусловленные действием источника ЭДС Е₃. Схема представлена на рисунке 7.7.

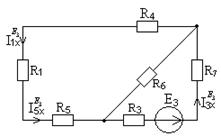
Рисунок 7.7

Ток ветви источника 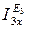равен:

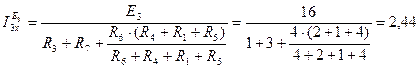А.

По правилу разброс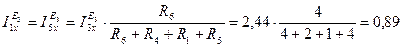а:

А.

Определяем токи I_1x^J и I_5x^J , обусловленные действием источника тока J . Схема представлена на рисунке 7.8.

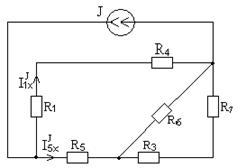
Рисунок 7.8

По правилу разброса:

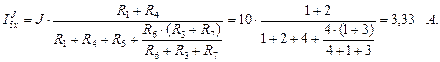
Ток I_1x^J определяем применяя первый закон Кирхгофа:

I_1x^J= J - I_5x^J= 10- 3,33=6,67 A.

Согласно методу наложения определяем алгебраическую сумму токов:

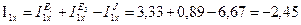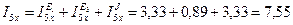A;

A.

Напряжение холостого хода:

U_xx=E₂+E₁-R₁I_1x-R₅I_5x= 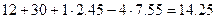B.

Определяем входное сопротивление R_вх . Входное сопротивление R_вх- это сопротивление пассивного двухполюсника. Для его определения все источники в схеме активного двухполюсника (см. рис. 7.5) необходимо исключить. Схема для определения R_вх изображена на рисунке 7.9.

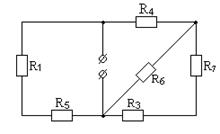
Рисунок 7.9

R_вх=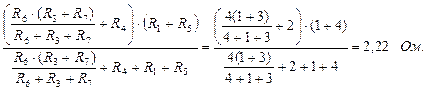

Согласно теореме об эквивалентном генераторе определяем ток I₂:

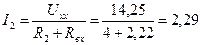А.

7.2 Рассчет разветвленной электрической цепи гармонического тока.

7.2.1 Расчет цепи гармонического тока при отсутствии магнитной связи между катушками.

Для цепи, показанной на рисунке 7.10 определить комплексным методом токи и напряжения ветвей, проверить выполнение баланса мощностей. Построить векторную диаграмму и графики мгновенных значений e(t) , i(t).

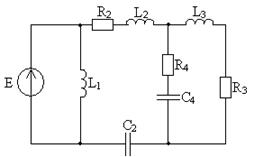
Рисунок 7.10

Параметры данной электрической цепи имеют следующие значения:

E=120 B; 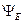=30 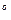; f=200 Гц;

L₁=8 мГн; R₂=1 Ом; L₂=5.59 мГн;

C₂=66,5 мкФ; R₃=3 Ом; L₃=3,194 мГн;

C₄=100 мкФ; R₄=6 Ом.

Решение:

Определяем угловую частоту: .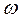

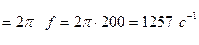Вычисляем индуктивные и емкостные сопротивления:

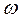
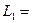
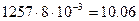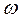
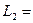
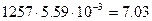Ом;

Ом;

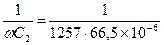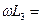
=11,96 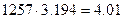Ом;

Ом;

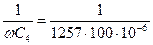=7,96 Ом.

Вычисляем комплексные сопротивления ветвей:

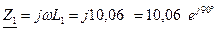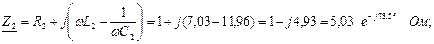
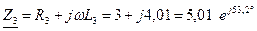Ом;

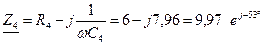Ом;

Ом.

Как видно из рисунка 7.11, данная цепь представляет собой последовательно- параллельное соединение.

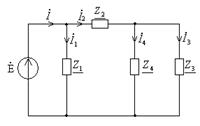
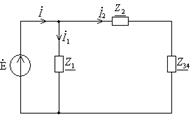
Рисунок 7.11 Рисунок 7.12

Комплексная форма ЭДС:

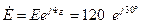В.

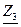Ветви и 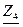соединены параллельно. Определяем их эквивалентное сопротивление:

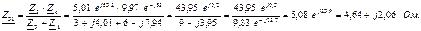
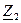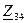Сопротивления и соединены последовательно, что видно из рисунка 7.12.

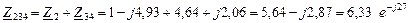Ом.

Определяем токи в ветвях:

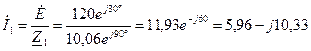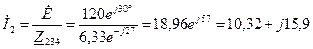(А);

(А).

Ток 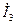определяем по формуле разброса:

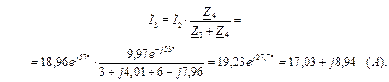
Ток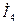и и 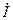определяем по первому закону Кирхгофа:

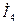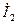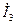= - =10,32+j15,9 – 17,03 – j8,94= - 6,71+j6,96=9,67e^j134 (А);

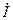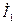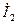= + =5,96 – j10,33+10,32+j15,9=16,28+j5,57=17,21e^j18,9 (A).

Определяем напряжения ветвей:

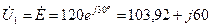(В);

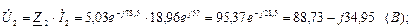
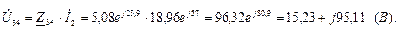
Правильность расчета проверяем по второму закону Кирхгофа: ;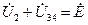

88,73 – j34,95+15,23+j95,11=103,96+j60,16;

103,96+j60,16 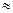103,92+j60;

Второй закон Кирхгофа выполняется, следовательно напряжения ветвей найдены правильно.

Проверим выполнение баланса активных и реактивных мощностей.

Комплекс полной мощности, вырабатываемой источником:

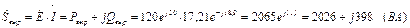
Вычисляем комплексы полных мощностей, потребляемых ветвями:

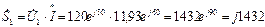(ВА);

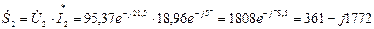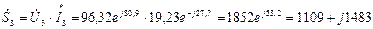(ВА);

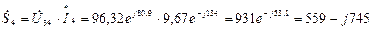(ВА);

(ВА).

Мощность, потребляемая всей цепью:

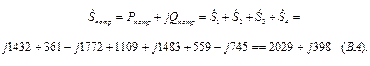
Баланс активных мощностей: Р_выр=Р_потр ; 2026 (Вт) 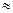2029 (Вт).

Баланс реактивных мощностей: Q_выр= Q_потр ; 398 (Вт) = 398 (Вт).

Примечание: в уравнениях баланса активных и реактивных мощностей погрешность не должна превышать 5%.

Таким образом, баланс активных и реактивных мощностей выполняется , что подтверждает правильность расчета токов и напряжений электрической цепи.

Построим векторную диаграмму.

Векторную диаграмму для разветвленной цепи строят согласно уравнениям, составленным по законам Кирхгофа:

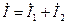; (7.9)

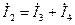; (7.10)

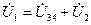. (7.11)

Для построения векторной диаграммы используют действующие значения токов и напряжений на участках цепи, а также углы сдвига фаз между ними. Следует напомнить, что на векторной диаграмме сдвиг фаз 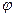откладывают от тока к напряжению, причем, если угол 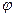>0 (индуктивный характер), его откладывают против часовой стрелки, а если 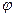<0 (емкостный характер)- по часовой стрелке.

Запишем действующие значения напряжений, токов и углы сдвига фаз:

U₁=E=120 B; I₁=11,93 A; 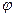₁=90^o;

U₂=95,37 B; I₂=18,96 A; 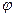₂= - 78,5^o;

U₃₄=96,32 B; I₃=19,23 A; 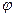₃=53,2^o;

I₄=9,67 A; 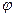₄= - 53^o.

I=17,21 A;

Выбрав масштабы напряжения и тока, векторную диаграмму для разветвленной цепи начинаем строить с последнего разветвления. Так как третья и четвертая ветви соединены параллельно, то первым отложим вектор напряжения U₃₄ и построим относительно него токи I₄ и I₃ под углами сдвига фаз 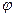₄ и 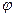₃, как показано на рисунке 7.13.

Геометрическая сумма токов I₄ и I₃ равна току I₂,согласно уравнению (7.10). Затем ,согласно уравнению (7.11), к вектору U₃₄ прибавим вектор напряжения второй ветви , повернув его на угол 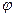₂ относительно тока I₂. Сложив геометрически U₃₄ и U₂, получим напряжение U₁ , равное ЭДС Е.

Наконец, к вектору I₂ ,согласно уравнению (7.9), прибавим вектор тока I₁ , построенный под углом 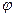₁ относительно напряжения U₁ . Геометрическая сумма I₁ и I₂ равна току источника I.

Итак, диаграмма построена в следующей последовательности:

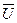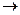
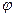_{34 4} .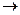

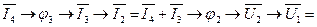
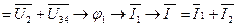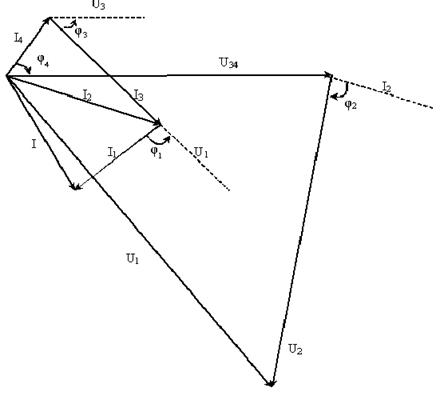
Рисунок 7.13

Запишем мгновенные значения ЭДС e(t) и тока в ветви источника i(t) и построим их графики, которые показаны на рисунке 7.14.

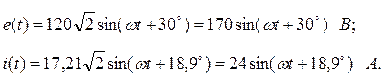
Ось ωt может быть размечена в радианах или градусах (например, 30^º соответствует 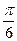радиан, а 18,9^º соответствует 0,11π радиан). Положительная начальная фаза откладывается влево от начала координат, отрицательная - вправо. Из этой точки начинается положительная полуволна синусоиды.

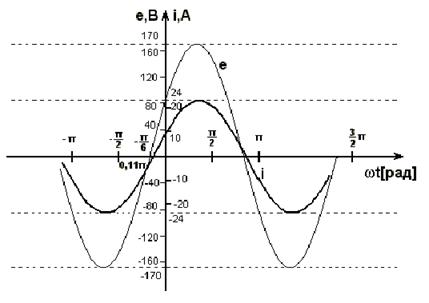
Рисунок 7.14

7.2.2 Расчет электрической цепи гармонического тока при наличии индуктивной связи между катушками

Если изменение тока в одной из катушек индуктивности приводит к появлению ЭДС в другой, то говорят, что эти две катушки имеют магнитную связь или индуктивно связаны, а возникающую ЭДС называют ЭДС взаимной индукции. ЭДС взаимной индукции должна быть учтена при расчете электрической цепи. Для расчета разветвленной цепи применяют законы Кирхгофа, метод контурных токов или специальный прием, называемый «развязкой» индуктивной связи.

Для примера воспользуемся схемой предыдущей задачи (см. рис. 7.10), введя индуктивную связь между катушками второй и третьей ветвей, как показано на рисунке 7.15.

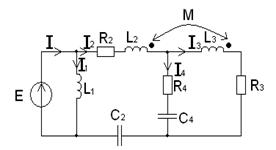
Рисунок 7.15

Значения параметров источника и сопротивления элементов данной цепи заданы следующие:

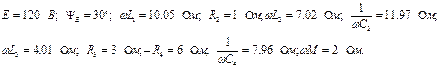
Составим систему уравнений в комплексной форме по законам Киргофа. Задаемся направлениями токов в ветвях. Направление обхода контуров выберем по часовой стрелке.

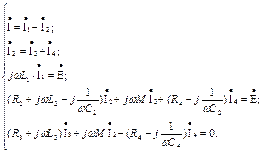(7.12)

Токи I₂ и I₃ направлены одинаково относительно одноименных зажимов катушек L₂ и L₃, т.е. имеет место согласное включение. (В случаи разного направления токов I₂ и I₃ относительно одноименных зажимов будет иметь место встречное включение). Перед слагаемым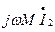и и 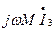поставлен в уравнениях знак плюс, т.к. направления токов I₂ и I₃ совпадают с направлением обхода контуров и включение согласное.

Рассмотрим прием «развязки» индуктивной связи, суть которого состоит в том, что схему, содержащую индуктивные связи заменяют эквивалентной схемой без индуктивных связей. Общее правило развязки индуктивной связи заключается в следующем: если две индуктивно связанные ветви подключены к узлу разветвления электрической цепи своими одноименными зажимами, то при «развязывании» индуктивной связи в эти ветви дополнительно вводится индуктивность «-М », а в свободную ветвь (также подключенную к этому узлу) вводится «+М». Если индуктивно связанные ветви подключены к узлу своими разноименными зажимами, то при «развязывании» в эти ветви вводится «+М», а в свободную ветвь «-М».

На рисунке 7.16 приведем в качестве примера несколько различных схем с двумя индуктивно связанными катушками и соответствующие им «развязки».

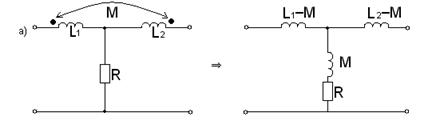
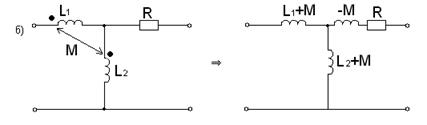
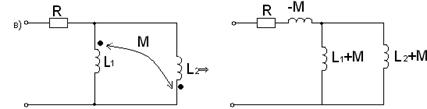
Рисунок 7.16

Применим для расчета токов схемы (см. рис.7.15) метод индуктивной развязки. Произведя «развязку» индуктивной связи, получим схему показанную на рисунке 7.17.

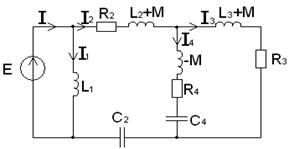
Рисунок 7.17

Полученная схема представляет собой последовательно-параллельное соединение. В этой схеме токи ветвей будут такими же, как и в исходной схеме (см. рис. 7.15), а напряжения не сохраняются.

Вычисляем комплексные сопротивления:

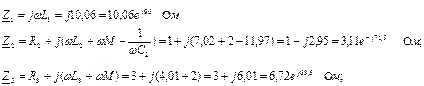
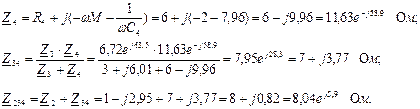
Определяем токи:

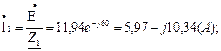
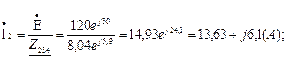
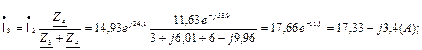
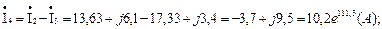
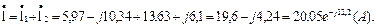
Правильность расчета токов можно проверить, подставив найденные токи в систему уравнений, составленную по законам Кирхгофа (7.12).

Определяем напряжения ветвей.

Схема магнитной развязки (см. рис. 7.17) используется только для расчета токов. Для определения напряжений ветвей обратимся к исходной схеме (см. рис.7.15).

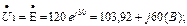
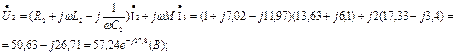
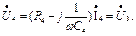
Составим баланс мощностей для второй и третьей ветвей.

Вычисляем мощности, поступающие во вторую и третью ветви от источника:

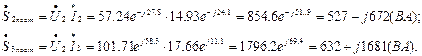
Определяем мощности, потребляемые элементами ветвей:

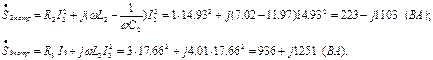
Определяем мощности, переносимые магнитными потоками, вследствие явления взаимоиндукции:

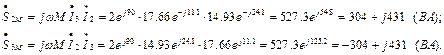
Мощность, поступающая в ветвь от источника равна сумме мощности потребляемой элементами этой ветви и мощности переносимой магнитным полем:

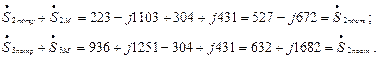
Мощност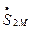и и 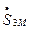могут быть представлены и как вырабатываемые источниками во второй и третьей ветвях, ЭДС которых равна ЭДС взаимоиндукции :

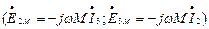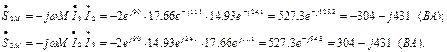
Тогда баланс мощностей будет иметь вид: