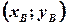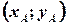Транспортна задача (тз)

Є декілька виробників деякої однорідної продукції (цегла, цукор, харчові напівфабрикати, тощо) і декілька споживачів цієї продукції. Виробники в деяких об’ємах виробляють продукцію, а споживачі в деяких своїх об’ємах її споживають. Кожний виробник може постачати свою продукцію в принципі кожному споживачеві, що пов’язано з транспортними витратами. Перевезення продукції здійснюється певними шляхами, що накладає обмеження стосовно пропускних спроможностей.

Треба скласти план перевезення продукції, за яким були б задоволені потреби споживачів та транспортні витрати на перевезення продукції при цьому були б мінімальними.

Вихідні дані відповідають транспортній таблиці:

В₁ В₂ В₃ - споживачі

11 17 12

6 10	10 7	5 12
7 5	10 13	8 9

виробники

А₁

15

А₂

25

Праві верхні куточки таблиці – транспортні витрати – це вартість перевезень від виробника до споживача одиниці продукції.

В лівих куточках – пропускні спроможності.

Перед початком розв’язання ТЗ повинна бути збалансована: сумарний запас = сумарним потребам (якщо це не так, то є певні методи збалансування ТЗ).

Математична модель транспортної задачі.

Позначимо m – кількість виробників, n – кількість споживачів.

а₁, а₂, …, а_m – об’єми виробництва

b₁, b₂, …, b_n – потреби (об’єми споживання)

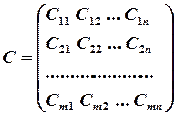– транспортні витрати, 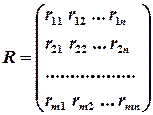– пропускні спроможності,

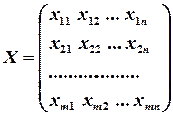– змінні, x_ij - об’єм перевезень від і-го виробника до j-го споживача (кількість продукції від A_i до B_j)

Цільова функція – функція сумарних транспортних витрат

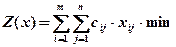
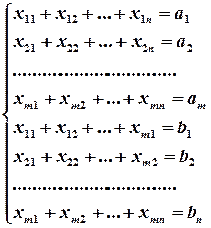Обмеження (умови)

Уся продукція виробника має бути вивезена і

усі потреби мають бути задоволені..

Умова невід’ємності змінних: всі .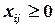

Це є математична модель транспортної задачі без урахування обмежень на пропускні спроможності. У математичній моделі повної транспортної задачі (з урахуванням обмежень на пропускні спроможності) все абсолютно те саме, що і в ТЗ без обмежень, тільки до умов добавляються нерівності: всі .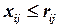

Аналіз і методи розв’язання транспортної задачі розглядаються окремою математичною дисципліною, яка має назву „Математичне програмування”. Зауважимо, що при побудові математичної моделі задачі природньо виникли структури данних, що мають назву матриці.

4. Задача про побудову водокачки.

Фірма має два підприємства, технологія виробництва яких вимагає використання води. Ці виробництва розташовані в пунктах Аі В. Повз них протікає річка, берег якої можна вважати прямою лінією. На березі потрібно побудувати водокачку і прокласти автономні водопроводи до кожного з пунктів Аі В. Вартість водопроводу прямо пропорційна його довжині. Треба визначити місце побудови водокачки, якому б відповідала мінімальна сумарна вартість водопроводу.

річка

Побудуємо математичну модель задачі. Для її побудови введемо декартову систему координат на площині.

y

	В

150

А

100

		Х

x

Берег річки

Позначимо через 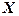невідоме поки що місце побудови водокачці. У введеній системі координат точка 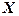має бути розташована на осі 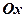. Отже, точці 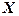буде відповідати значення дійсної змінної 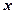. Тоді сумарна відстань від точки 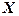до точок 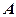і 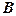буде визначатися формулою:

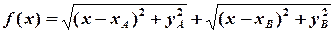
Тепер знайти потрібну точку 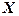— це все одно, що знайти значення 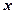, яке відповідало б мінімальному значенню функції 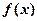, і задача про побудову водокачки зведена, таким чином, до суто математичної задачі:

.

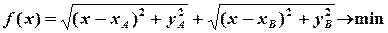Побудована тут функція 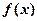зветься ірраціональною.

Цю задачу можна розв’язати за допомогою геометричних міркувань.

Побудуємо точку 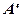, симетричну 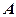відносно прямої 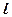, що визначає лінію берега. З’єднаємо 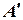з 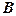. Нехай 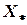— це точка перетину 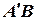з 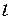.Стверджується, що ця точка є шуканою. Такий спосіб розв’язання задачі притаманний аналітичній геометрії, яка використовує геометричні міркування і алгебраїчні перетворення.

Вправа. Довести справедливість твердження щодо точки .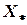

5. Задача про найменшу собівартість деталей.

На деякому підприємстві вартість деталей, що виготовляються понаднормово визначається за формулою: 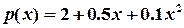. Треба визначити кількість деталей, виготовлених понаднормово, для якої собівартість однієї деталі найменша:

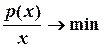
Вираз 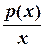, що присутній у формальному запису цієї задачі — це функція, яка зветься дробово-раціональною. Частинним випадком дробово-раціональної функції є дробово-лінійна функція, наприклад, така: 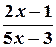, а найпростішою дробово-раціональною функцією є функція обернено-пропорційної залежності 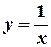, графіком якої є крива, що зветься гіперболою.

6. Внески під простий процент.

Введемо позначення:

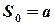- початкова величина внеску,

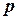- ставка (процент).

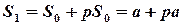- сума після першого року.

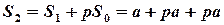- величина внеску після 2 року.

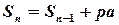- величина внеску після n –го року.

Цю модель можна використовувати при розв’язанні таких задач:

1) при заданих 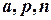обчислити ;

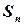2) при заданих 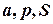знайти найменше 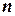, при якому ;

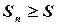В цій моделі з’являється конструкція, відома в математиці під назвою арифметичної прогресії.

Арифметична прогресія - це послідовність чисел ,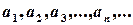

в якій кожне наступне число більше від попереднього на фіксовану величину d, яка називається різницею арифметичної прогресії:

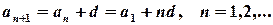
Справедлива формула для суми n перших членів арифметичної прогресії:

.

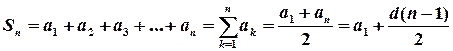Вправа. Довести справедливість наведеної формули і за її допомогою дати розв’язання поставлених задач щодо величини внеску.

7. Внески під складний процент.

Ситуація дуже схожа з внесками під простий процент з невеликою відмінністю:

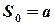- початкова сума,

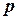- ставка (процент).

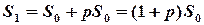- сума після першого року.

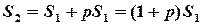- величина внеску після 2 року.

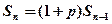- величина внеску після n-го року.

В цій моделі з’являється математична конструкція, яка називається геометричною прогресією.

Геометрична прогресія – це послідовність чисел 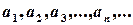, в якій кожний наступний елемент дорівнює попередньому, помноженому на сталу величину q, яка називається знаменником геометричної прогресії:

.

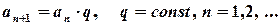Сума перших n членів геометричної прогресії обчислюється за формулою

.

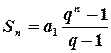
Вправа. Довести справедливість наведеної формули.

Для математичної моделі задачі про складний процент можна розв’язувати такі самі задачі, як і в попередньому випадку. Для розв’язання цих задач треба володіти поняттями степеневої, показникової та логарифмічної функцій.

Якщо знаменник q геометричної прогресії більше 0 і менше 1, така геометрична прогресія називається нескінченно спадною.

Для нескінченно спадної геометричної прогресії можна підрахувати суму всієї нескінченної кількості її членів:

.

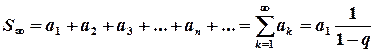Можливість такого „нескінченного підрахунку” зумовлена міркуваннями, пов’язаними з поняттям границі числової послідовності. Якщо ми розглянемо суму перших n членів геометричної прогресії і будемо послідовно збільшувати значення n, то доданок 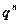буде необмежено зменшуватися до 0, „зникати”, як прийнято казати в математиці, а отже величина 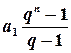буде необмежено наближатись до величини 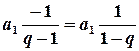, яку й прийнято вважати сумою всіх членів геометричної прогресії.

8. Десяткові періодичні та звичайні дроби.

Наведену вище формулу суми всіх членів геометричної прогресії можна використати для переведення десяткових періодичних дробів у звичайні.

Приклад 1.

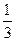= 0,333... 3... = 0,(3) =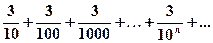

Маємо геометричну прогресію з a₁ = 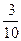, q = .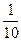

Отже

= .

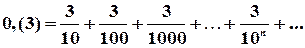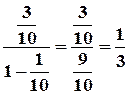Приклад 2.

0,2 (13) = 0,2 + .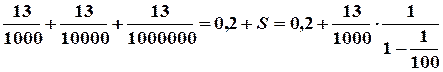

Вправа. Завершити перетворення отриманого виразу у звичайний дріб.

Висновки. Застосування математики при розгляді економічних, соціологічних, політичних та інших питань ґрунтується на методі математичного моделювання. Основною частиною математичних моделей є залежності, рівняння або функції, між величинами, які “відповідають” за той чи інший аспект розглядуваного процесу. Поняття рівняння є центральним поняттям розділу математики, який називається алгеброю. Поняття функціональної залежності є основним поняттям математичного аналізу.

Зовсім не випадково, але й не внаслідок підбору, розглянуті задачі виявились пов’язаними з пошуком найменших або найбільших значень деяких функцій, а ще важливіше, –пошуком відповідних значень аргументу – точок мінімуму та максимуму функцій. З цього приводу відомі близькі за змістом висловлювання великих математиків Готфріда Вільгельма Лейбніца і Леонарда Ейлера, які ми об’єднаємо в єдину тезу Лейбніца-Ейлера: “Оскільки будівля всього світу є досконалою і споруджена премудрим Творцем, то в світі не відбувається нічого, у чому не можна було б побачити смисл якого-небудь мінімуму або максимуму”.