Критерий Дарвина-Уотсона. Алгоритм выполнения. Практическое применение

В прикладных задачах всегда начинают исследование с лин ф-ии, затем берут либо степенную, либо показательную. Затем полином второй степени и в редком случае третьей.

Помимо проверки модели с помощью критериев значимости, которые учитывают влияние выявленных факторов на изменение результата, всегда исследуют остаток модели и поведение индивидуальных значений в этом остатке.

В случае, если прослеживается коррелированность между индивидуальными значениями остатка (u_i), то есть между 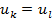( 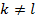), говорят о возникновении возможной автокорреляции, которая проверяется с помощью различных тестов (критериев).

Самым простым критерием проверки сущ-ия автокорреляции в остатках явл-ся критерий Дарбина-Уотсона (обозначаем d или dw).

Алгоритм dw-критерия:

1. Выдвигается гипотеза, рассчитывается статистика, лежащая в основе критерия.

2. Берется таблица критических значений для статистики Дарбина-Уотсона (dw –критерий).

3. Производится сравнение рассчитанного значения статистики с табличными значениями и опр-ся область, в которую попадает рассчитанное значение статистики Дарбина-Уотсона.

На основе информации по зонам шкалы делают вывод о наличии или отсутствии автокорреляции.

В случае наличия делают вывод о положительной или отрицательной автокорреляции.

Однако сущ-ют зоны, в которых с помощью критерия Дарбина-Уотсона нельзя опр-ть ни наличие, ни отсутствие автокорреляции.

В случае обнаружения автокорреляции нельзя использовать классический МНК.

Автокорреляция остатков порядка d равна коэф-ту корреляции, рассчитанному между исходными остатками модели и лаговыми остатками порядка d.

Причиной появления в остатках достоверной автокоррлеции первого порядка явл-ся наличие в остатках тенденций, вызванных некачественной спецификацией модели (см в 6 этапах эк моделирования, где возникает проблема спецификации, и с чем она связана).

Последствия наличия автокорреляции первого порядка заключаются в следующем: модель плохо специфицирована, и требуется с помощью подходящих инструментов ее улучшить (через подбор значения R², см компьютерные распечатки); ошибка явл-ся завышенной, а достоверность модели заниженной.

Непосредственно критерий Дарбина-Уотсона состоит из трех этапов:

1. Вычисляется статистика Дарбина-Уотсона:

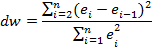
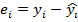
2. Опр-ся по таблицам нижняя и верхняя пороговые значения (d_н , d_в), зависящие от числа измерений, уровня значимости и числа объясняемых факторов модели).

3. Проверяются диапозоны попадания статистики Дарбина-Уотсона соответствующим выводам.

a)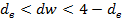

b)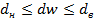

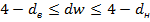
c)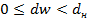

d)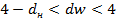

Для каждой области формулируется свой вывод:

a) Нулевая гипотеза об отстуствии автокорреляции принимается;

b) Нулевая гипотеза об отсутствии автокорреляции не принимется и не отвергается (область неопределенности);

c) Нулевая гипотеза об отсутствии об автокоррлеяции отвергается, сущ-ет положительная автокорреляция остатков;

d) Нулевая гипотеза об отсутствии об автокоррлеяции отвергается и утверждается, что имеется отрицательная автокорреляция остатков.

Коэф-т автокорреляции может принимать значения от -1 до +1 включительно. На его основе на графиках и корреляционном поле можно построить разброс точек.

Критерий Дарбина-Уотсона, к сожалению, не дает однозначного ответа о сущ-ии или отсутствии автокорреляции на всех участках (в частности зона b). Следовательно в случае попадания в зону b, построенная изначально модель парной регрессии (лин или нелин) не будет иметь практического применения.

Автокорреляция явл-ся хар-кой временного ряда. Плоэтому при расчете статистики Дарбина-Уотсона часто i заменяют на t, то есть:

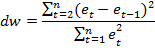
Сущ-ет два опр-ия коэф-та автокорреляции: прямое и обратное. Прямое – коэф-т автокорреляции показывает степень влияния текущих значений временного ряда на его будущие значения.

Обратное – коэт-т автокорреляции показывает степень влияния будущих значений временного ряда на его текущие значения.