Магнитно - связанные цепи

Магнитная и индуктивная связь возникает в цепях, содержащих катушки индуктивности, близко расположенные друг к другу и оказывающие взаимное влияние своими магнитными полями. Магнитная связь широко применяется в усилительной технике (связанные контуры, усилители с трансформаторной связью и т. п.) . Представим себе две катушки в виде тонких колец с числом витков и (рисунок 2. 14) .

Если в первой катушке течет ток , то возникает магнитный поток , пронизывающий первую катушку, его часть , пронизывает вторую катушку.

Рисунок 2. 14

Индуктивность первой катушки и взаимная индуктивность между первой и второй катушками определяется выражениями

,

где и — потокосцепление самоиндукции и взаимоиндукции. Магнитный поток измеряется в Веберах (Вб), а взаимная индуктивность — в Генри (Гн) . Аналогично, рассматривая магнитный поток, создаваемый током второй катушки, можно записать

,

причем, . Можно показать, что для изотропной ( однородной, линейной) в магнитном отношении среды (например, воздуха) . Для оценки степени магнитной связи между цепями вводят коэффициент связи , который находят из соотношения

,

откуда

. (2. 29)

Так как , , то коэффициент связи всегда меньше единицы. Он может быть близок к единице, если катушки расположены очень близко друг от друга или находятся на общем ферромагнитном сердечнике.

Для того, чтобы определить знак напряжения взаимоиндукции, введем понятие : одноименные зажимы индуктивно связанных катушек. Одноименные зажимы определяют, руководствуясь следующим правилом : при одинаковом направлении токов относительно этих зажимов магнитные потоки самоиндукции и взаимной индукции в каждой катушке должны суммироваться. Одноименные зажимы отмечают какими либо значками (например, точками). Их часто называют началами обмоток. Одноименные зажимы легко определяются, если известно направление обмотки катушек, как например, на рисунке 2. 15, на котором изображены две катушки и , намотанные на общий сердечник.

Рисунок 2. 15

Подключим к первой катушке источник напряжения, при этом возникает ток . Согласно принципу Ленца, во второй катушке, замкнутой на гальванометр, должен возникнуть ток , который возбудит магнитный поток, ослабляющий магнитный поток взаимной индукции. Направление тока определяется по правилу правого буравчика. При этом отклонение стрелки гальванометра будет положительным и, значит, напряжение взаимной индукции направлено от начала второй катушки к ее концу. Итак, будем считать, что если ток первой катушки втекает в ее начало, то напряжение взаимной индукции на второй катушке направлено от ее начала к ее концу. Напряжение и ЭДС взаимной индукции связаны между собой соотношением

,

.

Если токи изменяются по гармоническому закону, комплексные напряжения взаимной индукции определяются аналогично напряжению самоиндукции :

.

Величину называют комплексным сопротивлением взаимной индуктивности : . Ознакомившись с основными понятиями индуктивно связанных цепей, можно перейти к их расчету.

Рассмотрим вначале так называемое согласное последовательное включение двух катушек (рисунок 2. 16, а) , в котором ток протекает в одинаковом направлении относительно начал.

а) б)

Рисунок 2. 16

Благодаря этому напряжение взаимной индукции и имеют такое же направление, как напряжения и на катушках (от начала к концу). Поэтому можно записать: .

Общее напряжение .

Отсюда находим комплексное сопротивление цепи : .

Как видно из этой формулы, полное сопротивление при согласном соединении катушек становится больше, чем оно было бы при отсутствии магнитной связи. Величина представляет собой эквивалентную индуктивность цепи. При и К_св =1 она равна 4L. Аналогично можно показать, что при встречном включении катушек (рисунок 2.16 б) полное сопротивление будет меньше, а эквивалентная индуктивность цепи будет равна . Измеряя по отдельности индуктивности магнитно-связанных катушек, а затем индуктивность их последовательного соединения, можно установить расположение их начал.

В радиотехнических устройствах часто применяют так называемые воздушные трансформаторы (рисунок 2.17), например, в связанных колебательных контурах.

Рисунок 2. 17

Трансформатор представляет собой устройство, состоящее из двух магнитно-связанных катушек (или обмоток). Обмотку трансформатора (L₁ ,r₁) , подключаемую к источнику сигнала , называют первичной, а другую , индуктивно с ней связанную, вторичной (L₂ ,r₂ ) . Соответственно. напряжения и токи в обмотках именуются первичными (U₁ ,I₁ ) и вторичными (U₂ ,I₂ ). Найдем входное сопротивление воздушного трансформатора, нагруженного сопротивлением . Составим уравнение по второму закону Кирхгофа для первичной и вторичной цепи

;

.

В этих уравнениях значение представляет собой ЭДС, индуктированную вторичным током в первичной цепи, а — ЭДС, индуктированную первичным током во вторичной цепи.

Знак “минус” в этих уравнениях обусловлен различными направлениями токов относительно начал обмоток. После ряда простых действий найдем

,

В этих уравнениях — комплексное сопротивление первичной цепи; — комплексное сопротивление вторичной цепи; — комплексное сопротивление взаимной индуктивности; и — вносимые сопротивления.

Полученным уравнениям для токов I₁ и I₂ соответствуют одноконтурные схемы замещения воздушных трансформаторов, изображенные на рисунке 2. 18 для первичной цепи (рисунок 2. 18, а) и для вторичной цепи (рисунок 2. 18, б).

а) б)

Рисунок 2. 18

Величины вносимых сопротивлений определяются соотношениями

;

— активная составляющая вносимого сопротивления из вторичной цепи в первичную;

— реактивная составляющая вносимого сопротивления из вторичной цепи в первичную.

Аналогично для вторичной цепи вносимые сопротивления :

Знак "минус" в выражении для и свидетельствует о размагничивающем действии вторичной обмотки на первичную.

Величина входного сопротивления трансформатора определяется из соотношений:

, (2. 30)

где

.

Как показывает формула (2. 30), входное сопротивление на первичных зажимах зависит от параметров вторичной цепи и степени связи. Если вторичная цепь разомкнута или нет магнитной связи , то , .

Пример. Определить, как изменится эквивалентная индуктивность идеальной катушки , если вторая идеальная катушка , индуктивно связанная с первой, будет закорочена.

Для идеальных катушек .

Пользуясь формулой (2. 30), находим

.

Таким образом,

или, с учетом формулы (4.29),

.

Как видим, эквивалентная индуктивность уменьшается и стремится к нулю, если .

Воздушный трансформатор может быть представлен двухконтурной схемой замещения, изображенной на рисунке 2. 19. Эта схема получается непосредственно из схемы , изображенной на рисунке 17, после объединения в один узел одноименных зажимов и учета взаимной индуктивности М.

Рисунок 2. 19

В усилительной технике, например, в усилителях низкой частоты, применяются трансформаторы с ферромагнитным сердечником (рисунок 2. 20, а). Коэффициент связи между катушками при этом стремится к единице. Это значит, что магнитный поток практически полностью замыкается по сердечнику, не рассеиваясь в пространство. Строго говоря, трансформатор с ферромагнитным сердечником не является линейной системой из-за нелинейности характеристики намагничивания B = f (Н) , однако на практике такой трансформатор конструируют таким образом, чтобы нелинейность была мала и ею можно было пренебречь.

На рисунке 2. 20, а приведена схема трансформатора с ферромагнитным сердечником. При подключенной нагрузке (в режиме холостого хода) . Обычно индуктивность — большая, поэтому ток — маленький, напряжение , где — коэффициент трансформации. При подключении нагрузки в ней возникает ток, и согласно правилу Ленца, ток в первичной обмотке должен возрасти, чтобы скомпенсировать размагничивающее действие тока вторичной обмотки : , где — дополнительный ток, связанный с соотношением (условие компенсации размагничивающего действия ). Отсюда

.

С учетом предыдущих зависимостей

. (2. 31)

Учитывая формулу (2. 31), входную цепь нагруженного трансформатора можно заменить эквивалентной схемой рисунок 2. 20, б. Сопротивление называется сопротивлением нагрузки, приведенным к первичной обмотке. Очевидно, мощность нагрузки при этом остается неизменной.

а)

б)

Рисунок 2. 20

Такого же результата можно добиться, если вместо числа витков взять и при вместо сопротивления включить ,определяемое формулой (2. 31). При этом . Если сопротивление нагрузки комплексное, оно пересчитывается также по формуле (2. 31), куда вместо 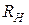следует подставить 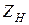. Это преобразование называется приведением трансформатора и его вторичной цепи к первичной обмотке, а сам трансформатор - приведенным. Например, если ко второй обмотке подключена емкость С , то ее приведенное комплексное сопротивление будет равно , откуда . Если трансформатор — понижающий ,то .Таким образом, выявлено важное свойство трансформатора –– изменять эквивалентное сопротивление нагрузки. Это свойство широко используется, для целей согласования и получения максимальной мощности в нагрузке.

В реальном трансформаторе наблюдается рассеивание магнитного потока в пространство, кроме того обмотки обладают активным сопротивлением. Для анализа устройств, содержащих трансформаторы, пользуются эквивалентной схемой замещения приведенного трансформатора, аналогичный рисунку 2. 20, б, в которой учитывают активные сопротивление обмоток и рассеивание магнитного потока (с помощью индуктивностей рассеивания). Очевидно, что комплексные сопротивления вторичной цепи надо пересчитать по формуле (2. 31). На схеме замещения трансформатора приведенной на рисунке 2. 20, б и - индуктивности рассеяния; и - активное сопротивление обмоток. Обычно индуктивность ; ее называют индуктивностью намагничивания.