Висота, проведена до гіпотенузи прямокутного трикутника, ділить її на відрізки у відношенні 9 : 16. Менший катет дорівнює 45 см. Знайдіть площу трикутника. Варіант 6
I частина (5 балів)
Завдання 1 – 5 мають по чотири варіанти відповіді, з яких тільки одна правильна. Оберіть правильну, на Вашу думку, відповідь. Правильне розв’язання кожного завдання оцінюється одним балом.
1. В колі проведені радіуси OА і OВ. Знайдіть градусну міру кута АОВ, якщо відповідна йому дуга дорівнює 70°.
А) 290°; Б) 140°;
В) 35°; Г) 70°.
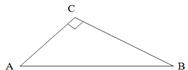2. В прямокутному трикутнику АВС, ВС = 
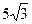см, АВ = 10 см. Знайдіть 
АВС.
А) 60°; Б) 30°;
В) 45°; Г) 90°.
3. Знайдіть середню лінію трапеції, якщо її менша основа дорівнює 5 см і становить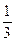 
її більшої основи.
А) 5 см; Б) 15 см;
В) 9 см; Г) 10 см.
4. Точки М і Р лежать відповідно на бічних сторонах АВ і ВС рівнобедреного трикутника АВС, причому МР || АС. Знайдіть периметр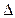 
АВС, якщо МР = 4 см, МВ = 5 см, АС = 12 см.
А) 27 см; Б) 42 см;
В) 31,2 см; Г) 36 см.
5. Знайдіть діагональ прямокутника, якщо одна з його сторін дорівнює 8 см, а периметр дорівнює 46 см.
А) 17 см; Б) 23 см;
В) 20 см; Г) 38 см.
ІІ частина (4 бали)
Розв’язання завдань 6 – 7 може мати короткий запис без обґрунтування. Правильне розв’язання кожного завдання оцінюється двома балами.
6. Сторона ромба утворює з діагоналями кути, які відносяться як 7 : 2. Знайдіть ці кути.
7. У прямокутнику, вписаному в коло, діагональ утворює зі стороною кут 32°. Знайдіть, на які частини поділяється коло вершинами прямокутника.
ІІІ частина (3 бали)
Розв’язання 8 завдання повинно мати обґрунтування. Потрібно записати послідовні логічні дії та пояснення. Правильне розв’язання завдання оцінюється трьома балами.
8. Катети прямокутного трикутника відносяться як 3 : 4, а висота ділить гіпотенузу на відрізки, різниця між якими 14 см. Знайдіть площу трикутника.
Варіант 7
I частина (5 балів)
Завдання 1 – 5 мають по чотири варіанти відповіді, з яких тільки одна правильна. Оберіть правильну, на Вашу думку, відповідь. Правильне розв’язання кожного завдання оцінюється одним балом.
1. У трикутнику АВС і DKP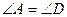 
, 
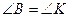. Знайдіть КР, якщо АВ = 12 см, ВС = 18 см, DK = 16 см.
А) 22 см; Б) 20 см;
В) 24 см; Г) 13,5 см.
2. Величина вписаного кута АВС дорівнює 70°. Знайдіть градусну міру дуги, що йому відповідає.
А) 140° ; Б) 70° ;
В) 35° ; Г) 290°.
3. Знайдіть периметр ромба ABCD, знаючи, що довжина його меншої діагоналі АС дорівнює 4 см, а тупий кут 120°.
А) 64 см; Б) 20 см;
В) 16 см; Г)40 см.
4. Середня лінія трапеції дорівнює 12 см, висота 4 см. Знайдіть площу трапеції.
А) 96см2 ; Б) 24 см2 ;
В) 48 см2 ; Г) 16 см2.
5. Кожний кут многокутника дорівнює 135°. Скільки сторін має цей многокутник?
А) 8 ; Б) 10;
В) 6; Г) 7.
ІІ частина (4 бали)
Розв’язання завдань 6 – 7 може мати короткий запис без обґрунтування. Правильне розв’язання кожного завдання оцінюється двома балами.
6. В прямокутний трикутник вписано коло з радіусом 4 см. Точка дотику ділить гіпотенузу на відрізки, довжини яких відносяться як 10 : 3. Знайдіть сторони трикутника.
7. У трапеції АВСD кут ВАD дорівнює 60°, висота ВК ділить основу АD на відрізки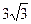 
см і 40 см. Знайти діагональ ВD.
ІІІ частина (3 бали)
Розв’язання 8 завдання повинно мати обґрунтування. Потрібно записати послідовні логічні дії та пояснення. Правильне розв’язання завдання оцінюється трьома балами.
8. Сторони трикутника дорівнюють 6 см, 25 см і 29 см. Знайдіть найменшу висоту трикутника.
Варіант 8
I частина (5 балів)
Завдання 1 – 5 мають по чотири варіанти відповіді, з яких тільки одна правильна. Оберіть правильну, на Вашу думку, відповідь. Правильне розв’язання кожного завдання оцінюється одним балом.
1.У трикутнику АВС і MNP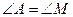 
, 
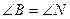. Знайдіть MN, якщо АВ = 18 см, ВС = 12 см, NP = 4 см.
А) 16 см; Б) 10 см;
В) 54 см; Г) 6 см.
2. Кут АВС – кут вписаний в коло. Градусна міра відповідної йому дуги дорівнює 140°. Знайдіть величину кута АВС.
А) 280°; Б) 70°;
В) 140°; Г) 220°.
3. Знайдіть периметр ромба АВСD, якщо відомо, що менша діагональ АС дорівнює 5 см, а кут між нею та стороною ромба дорівнює 60°.
А) 64 см; Б) 20 см;
В) 16 см ; Г) 25 см.
4. Знайдіть площу трапеції з основами 4 см і 6 см та висотою 3 см.
А) 15 см2; Б) 72 см2;
В) 9 см2; Г) 11 см2.
5. Скільки сторін має многокутник, якщо сума його внутрішніх кутів дорівнює 1980°?
А) 11; Б) 12;
В) 13; Г) 13.
ІІ частина (4 бали)
Розв’язання завдань 6 – 7 може мати короткий запис без обґрунтування. Правильне розв’язання кожного завдання оцінюється двома балами.
6. В прямокутний трикутник вписано коло. Точка дотику ділить один з катетів на відрізки довжиною 3 см і 9 см, починаючи від вершини прямого кута. Знайдіть другий катет та гіпотенузу.
7. В паралелограмі MNKP NMP=30°, висота NА ділить сторону КР на відрізки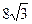 
см і 6 см. Знайдіть діагональ NP.
ІІІ частина (3 бали)
Розв’язання 8 завдання повинно мати обґрунтування. Потрібно записати послідовні логічні дії та пояснення. Правильне розв’язання завдання оцінюється трьома балами.
8. Знайдіть найбільшу висоту трикутника зі сторонами 5 см, 6 см, і 9 см.
Варіант 9
I частина (5 балів)
Завдання 1 – 5 мають по чотири варіанти відповіді, з яких тільки одна правильна. Оберіть правильну, на Вашу думку, відповідь. Правильне розв’язання кожного завдання оцінюється одним балом.
1. Кут між діагоналлю ромба і однією з його сторін дорівнює 50°. Знайдіть кути ромба.
А) 100°, 80°, 100°, 80°; Б)120°, 60°, 120°, 60°;
В) 50°, 130°, 50°, 130°; Г) 45°, 135°, 45°, 135°.
2. В трикутнику АВС висота ВD поділяє сторону АС на відрізки АD = 16 см і DС = 5 см. Знайдіть сторону ВС, якщо АВ = 20 см.
А) 13 см; Б) 9 см;
В) 7 см; Г) 11 см.
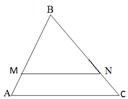3. Відрізок МN паралельний до сторони АС трикутника АВС. МN = 9 см, АС = 12 см, МВ = 7 см. Знайдіть довжину АВ.
А)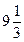 
см; Б) 2,7 см;
В) 28 см; Г) 29 см.
4. В трапеції АВСD ВС – менша основа. На основі АD взято точку К так, що ВК|| СD.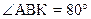 
, 
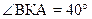. Знайдіть кут АВС.
А) 130°; Б) 120°;
В) 140°; Г) 60°.
5. Одна із сторін паралелограма на 10 см більша від другої, а периметр дорівнює 68 см. Знайдіть довжини сторін паралелограма.
А) 10 см, 22 см, 10 см, 22 см; Б) 22 см, 121 см, 22 см, 12 см;
В) 10 см, 12 см, 10 см, 12 см; Г) 29 см, 39 см, 29 см, 39 см.
ІІ частина (4 бали)
Розв’язання завдань 6 – 7 може мати короткий запис без обґрунтування. Правильне розв’язання кожного завдання оцінюється двома балами.
6. Катет прямокутного трикутника дорівнює 30 см, а гіпотенуза відноситься до другого катета, як 17 : 8. Знайдіть сторони трикутника.
7. Точки А і В ділять коло на дві дуги, менша з яких дорівнює 140°, а більша точкою М ділиться у відношенні 6 : 5, якщо рахувати від точки А. Знайдіть кут ВАМ.
ІІІ частина (3 бали)
Розв’язання 8 завдання повинно мати обґрунтування. Потрібно записати послідовні логічні дії та пояснення. Правильне розв’язання завдання оцінюється трьома балами.
8. В прямокутній трапеції основи дорівнюють 25 см та 32 см, а більша діагональ є бісектрисою гострого кута. Знайдіть площу трапеції.
Варіант 10
I частина (5 балів)
Завдання 1 – 5 мають по чотири варіанти відповіді, з яких тільки одна правильна. Оберіть правильну, на Вашу думку, відповідь. Правильне розв’язання кожного завдання оцінюється одним балом.
1. Діагональ ромба утворює з однією із сторін кут 25° . Знайдіть більший кут ромба.
А) 100°; Б) 130°;
В) 50°; Г) 155°.
2. Втрикутнику АВС довжина сторони ВС дорівнює 15 см, а проекції сторін АВ і ВС на сторону АС відповідно дорівнюють АD = 5 см, DС =9 см. Знайдіть довжину сторони АВ.
А) 13 см; Б) 12 см;
В) 10 см; Г) 19 см.
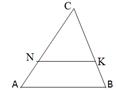3. В трикутнику АВС NК|| АВ, NК = 40 см, АВ = 50 см, СN = 48 см. Знайдіть АС.
А) 50 см; Б) 65 см;
В) 60 см; Г) 75 см.
4. В рівнобічній трапеції діагональ перпендикулярна до бічної сторони і утворює з більшою основою кут 25°. Знайдіть тупий кут трапеції.
А) 115°; Б) 155°;
В) 130°; Г) 105°.
5. Різниця довжин сторін паралелограма дорівнює 2 см, а периметр – 20 см. Знайдіть довжини сторін.
А) 6 см, 8 см, 6 см, 8 см; Б) 6 см, 4 см, 6 см, 4 см;
В) 5 см, 3 см, 5 см, 3 см; Г) 9 см, 11 см, 9 см, 11 см.
ІІ частина (4 бали)
Розв’язання завдань 6 – 7 може мати короткий запис без обґрунтування. Правильне розв’язання кожного завдання оцінюється двома балами.
6. Відношення катетів прямокутного трикутника дорівнює 12 : 5, а гіпотенуза – 39 см. Знайдіть сторони трикутника.
7. Точки М і N ділять коло на дві дуги, більша з яких дорівнює 220°, а менша точкою А ділиться у відношенні 5 : 2, якщо рахувати від точки М. Знайдіть кут NМА.
ІІІ частина (3 бали)
Розв’язання 8 завдання повинно мати обґрунтування. Потрібно записати послідовні логічні дії та пояснення. Правильне розв’язання завдання оцінюється трьома балами.