Основні поняття та визначення

На рис. 12а наведено шарнірно обперту балку – геометрично незмінювану систему. Всі три реакції визначаються з трьох умов рівноваги плоскої системи сил.

Використовуючи метод перерізів, легко знайти внутрішні силові фактори у будь якому перерізі балки.

Додамо ще одну шарнірну - рухому опору в перерізі С (рис. 12б). У наслідок цього система стала більш міцною та жорсткою, проте з погляду геометричної незмінюваності цей зв’язок зайвий. Тепер з трьох рівнянь рівноваги чотири реакції визначити неможливо. Балка, що зображена на рис. 12б, один раз статично невизначувана, т. я. реакції зв’язків не можуть бути однозначно визначені з рівнянь статичної рівноваги.

Таким чином, статично невизначуваними називаються системи, силові фактори в елементах яких тільки з рівнянь рівноваги визначити неможна. У таких системах зв’язків більше, ніж необхідно для рівноваги. Отже, деякі зв’язки виявляються в цьому розумінні так би мовити зайвими, а зусилля в них – зайвими невідомими. За числом зайвих зв’язків або зайвих невідомих зусиль установлюють ступінь статичної невизначуваності системи.

Ступінню статичної невизначуваності системи називається різниця між числом невідомих зусиль та кількістю незалежних рівнянь статичної рівноваги, які можна записати для даної системи.

Положення жорсткого стержня в просторі визначається шістьма незалежними координатами, інакше кажучи, жорсткий стержень володіє шістьма ступенями свободи. На стержень можуть бути накладені зв'язки, тобто обмеження, що обумовлюють його певне положення в просторі. Найбільш простими зв'язками є такі, при яких повністю виключаються те або інше узагальнене переміщення для деяких перерізів стержня. Накладення одного зв'язку знімає одну ступінь свободи з стержня як жорсткого цілого. Отже, якщо на вільний жорсткий стержень накладено шість зовнішніх зв'язків, то положення його в просторі як жорсткого цілого буде, за деякими виключеннями, визначено повністю і система з механізму, що володіє шістьма ступенями свободи, перетворюється в кінематично незмінну систему. Те число зв'язків, при якому досягається кінематична незмінність, носить назву необхідного числа зв'язків. Всякий зв'язок, накладений зверх необхідних, називають додатковим. Число додаткових зв'язків дорівнює ступеню статичної невизначуваності системи.

Зв'язки в рамах і стержньових системах ділять звичайно на зв'язки зовнішні і зв'язки внутрішні, або взаємні. Під зовнішніми зв'язками розуміються умови, що накладаються на абсолютні переміщення деяких точок системи. В разі плоскої системи у шарнірно - рухомій опорі є один зовнішній зв'язок, в нерухомому шарнірі - два, в жорсткому закріпленні - три. Просторове закріплення відповідає шести зовнішнім зв'язкам. Зовнішні зв'язки часто ділять на необхідні і додаткові. Наприклад, на рис.13а,б показана плоска рама, що має в першому випадку три зовнішні зв'язки, а у другому п'ять зовнішніх зв'язків.

Для того щоб визначити положення рами в площині як жорсткого цілого, необхідне накладення трьох зв'язків. Отже, в першому випадку рама має необхідні зовнішні зв'язки, а у другому, крім того, два додаткові зовнішні зв'язки.

Під внутрішніми, або взаємними, зв'язками розуміються обмеження, що накладаються на взаємні зміщення елементів рами. Тут також можна говорити як про необхідні, так і про додаткові зв'язки.

Так, наприклад, плоска рама, показана на рис. 14а, має необхідну кількість як зовнішніх, так і внутрішніх зв'язків між елементами. Це кінематично незмінна система.

Якщо будуть задані зовнішні сили, ми зможемо за допомогою рівнянь статики знайти як реакції опор, так і внутрішні силові фактори в будь-якому поперечному перерізі рами. У тій же рамі, показаній на рис. 14б, крім зовнішніх накладені два додаткові внутрішні зв'язки, які забороняють взаємне вертикальне і горизонтальне зміщення точок А і В. Система в цьому випадку двічі статично невизначувана (іноді додають: “внутрішнім образом"). У рамі рис. 13а,б також є внутрішні додаткові зв'язки. Контур рами повністю замкнутий. Розрізаючи його в будь-якому перерізі (рис. 15), ми, не порушуючи кінематичної незмінюваності, отримуємо можливість при заданих силах знайти внутрішні силові фактори в кожному перерізі рами.

Отже, розрізаючи замкнену раму, ми знімаємо додаткові зв'язки, тобто дозволяємо перетинам А і В повертатися і зміщуватися в двох напрямках один відносно одного.

Узагальнюючи, можна сказати, що замкнений плоский контур має три додаткові внутрішні взаємні зв’язки. Таким чином, рама, показана на рис. 13а, тричі статично невизначувана. Рама показана на рис. 13б, п'ять разів статично невизначувана (три рази внутрішнім образом і два рази – зовнішнім).

Статична невизначуваність може бути наслідком не тільки введення додаткової зовнішніх зв’язків, а й з умов утворення системи. Розглянемо раму, показану на рис. 16а. Очевидно, що реакції зовнішніх зв’язків (опор) легко визначити з рівнянь рівноваги.

Проте після цього рівняння рівноваги не дають змоги визначити всі силові фактори в елементах рами.

Розріжемо раму на дві частини й розглянемо рівновагу однієї з частин (рис. 16б). Дію відкинутої частини на залишену замінимо в кожному з перерізів розрізу трьома внутрішніми силовими факторами: осьовою силою , поперечною силою 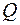та згинальним моментом . Отже, з трьох рівнянь рівноваги треба визначити дев’ять невідомих зусиль. Система шість разів статично невизначувана. Вона складається з двох замкнених безшарнірних контурів. Кожний замкнений контур тричі статично невизначуваний.

Метод сил

Для визначення зусиль у статично невизначуваних системах додатково до рівнянь статики складають так звані рівняння сумісності деформацій. Насправді, зайві зв’язки обмежують переміщення тих перерізів, до яких вони прикладені. Цю обставину й використовують для складання додаткових рівнянь, які разом з рівняннями статики дають змогу визначити всі силові фактори в елементах системи.

Розглянемо етапи розрахунку статично невизначуваної системи – заданої (вихідної) системи.

Визначаємо ступінь статичної невизначуваності заданої системи, тобто кількість зайвих зв’язків або зайвих зусиль.

Усуваючи зайві зв’язки і зовнішні навантаження, на основі заданої системи відокремлюємо кінематично незмінювану статично визначувану систему, яка зветься основною системою. Вибір зайвих зв’язків залежить від бажання того, хто робить розрахунок. Тому для однієї тієї самої статично невизначуваної вихідної системи можливі різні варіанти основних систем. Однак треба стежити за тим, щоб кожна з них була кінематично незмінюваною. Раціональний вибір основної системи спрощує розрахунок.

Отже, основною системою називається будь-який із статично визначуваних варіантів розглядуваної системи, здобутої звільненням її від зайвих зв’язків.

Завантажуємо основну систему заданим зовнішнім навантаженням і зайвими невідомими зусиллями, що заміняють дію усунених зв’язків. При цьому невідоме, що перешкоджає лінійному переміщенню, замінюється невідомою силою, доданої по напрямку цього переміщення. Невідоме, що перешкоджає повороту перерізу, замінюється невідомим моментом. Така система зветься еквівалентною системою.

Для того щоб отримана система була еквівалентною вихідній системі, невідомі зусилля треба добирати таким чином, щоб деформація основної системи не відрізнялася від деформації вихідної статично невизначуваної. Для цього прирівнюють до нуля переміщення точок прикладання невідомих зусиль у напрямі їх дії. Із добутих таким чином рівнянь знаходять значення зайвих невідомих.

Визначати переміщення відповідних точок основної системи можна будь-яким способом, проте найкраще загальними методами – за допомогою інтеграла Максвелла – Мора або способом Верещагіна.

Після знайдення зайвих невідомих зусиль, визначаємо реакції, будуємо епюри внутрішніх силових факторів. Повна (сумарна) епюра моментів , очевидно, може бути отримана шляхом складання вантажної епюри 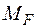і одиничних , помножених на величини :

,

при цьому ординати епюр обираються по всім ділянкам у відповідних точках з урахуванням знаків.

Епюри внутрішніх силових факторів також можна будувати традиційним способом. Визначивши опорні реакції для еквівалентної системи, записуємо рівняння внутрішніх силових факторів в окремих перерізах і будуємо епюри.

Після цього добираємо перерізи та перевіряємо міцність.

Наведена схема розрахунку має назву методу сил, оскільки як основні невідомі тут вибирають узагальнені зусилля зайвих зв’язків.

При розрахунку багатопрольотних нерозрізних балок (що опираються більше ніж на дві опори і не мають проміжних шарнірів) ця схема декілька змінюється. В якості основної системи в деяких випадках рекомендовано не усування зайвих зв’язків, а встановлення додаткових шарнірів, розташованих на осі балки над проміжними опорами. Таким чином перетворюється на нуль згинальний момент у даному перерізі й, отже, знижує ступінь статичної невизначуваності на одиницю. Такий шарнір називають додатковим або одиночним. При складанні додаткових рівнянь прирівнюються нулю взаємні кути повороту в місцях встановлення додаткових шарнірів.