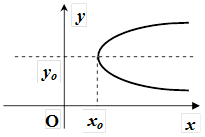
Параболи, симетричні відносно осі Ох
| рівняння | 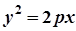 | 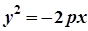 |
| координати фокуса | 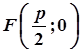 | 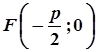 |
| рівняння директриси | 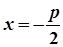 | 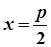 |
| рисунок | 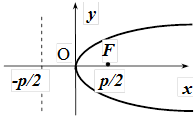 | 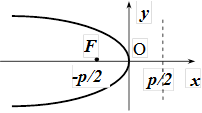 |
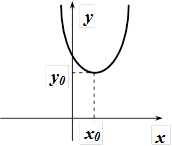
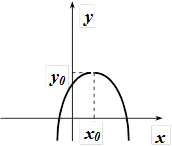
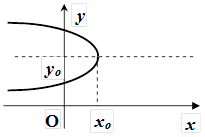
Параболи, симетричні відносно осі Оу
| рівняння | 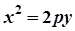 | 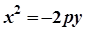 |
| координати фокуса | 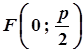 | 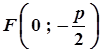 |
| рівняння директриси | 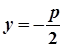 | 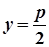 |
| рисунок | 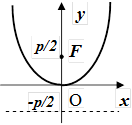 | 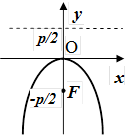 |
Зсунені криві
Коло 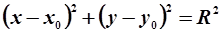
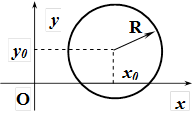
Еліпс 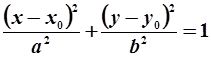 Гіпербола
Гіпербола 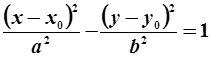
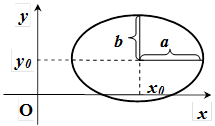
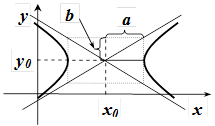
Параболи 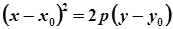
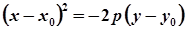
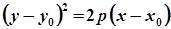
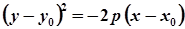
ГРАФІКИ ОСНОВНИХ ЕЛЕМЕНТАРНИХ ФУНКЦІЙ
Алгебраїчні функції
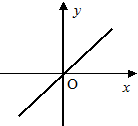
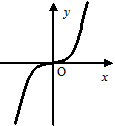
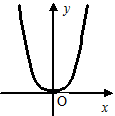
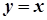
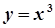 ,
, 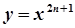
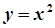 ,
, 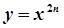
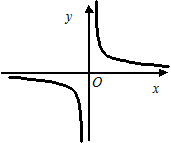
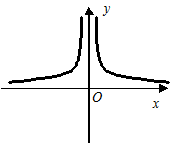
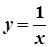 ,
, 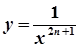
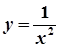 ,
, 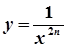
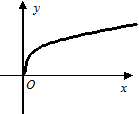
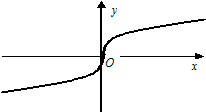

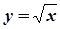 ,
, 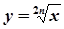
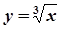 ,
, 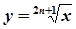
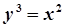 ,
, 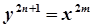
Трансцендентні функції
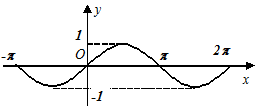
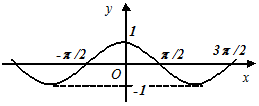
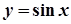
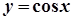
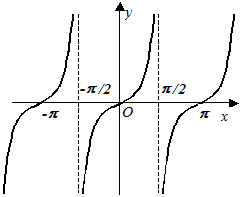
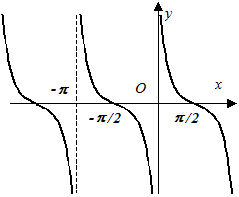
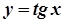
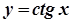
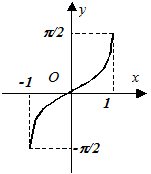
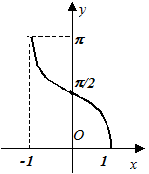
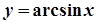
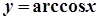
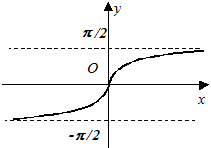
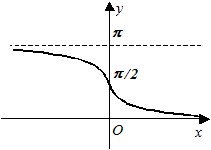
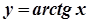
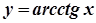
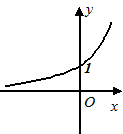
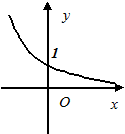
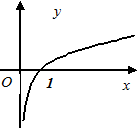

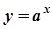 ,
, 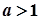
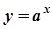 ,
, 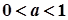
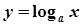 ,
, 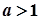
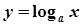 ,
, 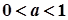
ГРАНИЦІ
Перша важлива границя 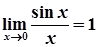 .
.
Друга важлива границя 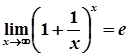 .
.
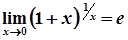 .
.
МЕТОДИ ОБЧИСЛЕННЯ ГРАНИЦЬ
У випадку невизначеності 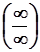 треба поділити чисельник та знаменник на найвищий степінь змінної.
треба поділити чисельник та знаменник на найвищий степінь змінної.
1) 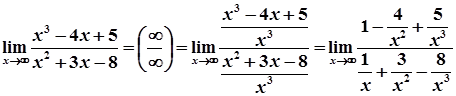 =
= 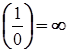 ;
;
2) 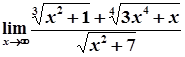 =
= 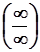 =
= 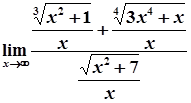 =
=
= 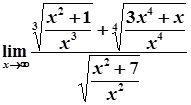 =
= 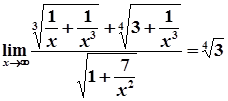 ;
;
3) 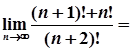
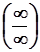 =
= 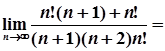
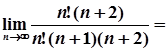
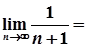
= 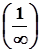 =0.
=0.
У разі невизначеності 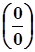 треба чисельник та знаменник розкладати на множники.
треба чисельник та знаменник розкладати на множники.
4) 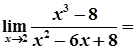
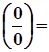
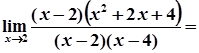
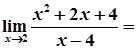
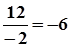 .
.
Якщо границя містить ірраціональність, позбутися її за допомогою формул скороченого множення; якщо невизначеність не зникне, а трансформується у 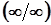 , поділити на старший степінь змінної (з урахуванням добування коренів).
, поділити на старший степінь змінної (з урахуванням добування коренів).
5) 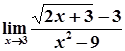 =
= 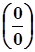 =
= 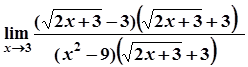 =
=
= 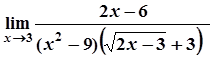 =
= 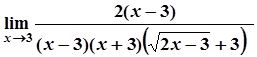 =
=
= 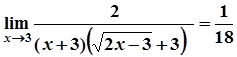 .
.
Якщо вираз має тригонометричні функції, перетворити суми тригонометричних функцій на добутки; множники, границя котрих не дорівнює 0 або 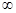 , замінити цими границями; для кожного множника, який прямує до 0, побудувати 1-у важливу границю.
, замінити цими границями; для кожного множника, який прямує до 0, побудувати 1-у важливу границю.
6) 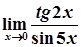 =
= 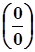 =
= 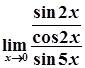 =
= 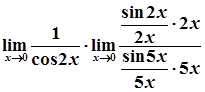 =
= 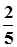 .
.
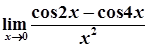 =
= 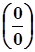 =
= 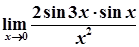 =
= 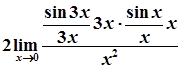 =
=
= 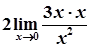 =6
=6
У випадку степенево-показникової функції (невизначеність 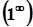 ) основу записати як суму 1 та нескінченно малої функції, побудувати другу важливу границю та перейти до границі у показнику.
) основу записати як суму 1 та нескінченно малої функції, побудувати другу важливу границю та перейти до границі у показнику.
7) 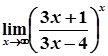 =
= 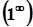 =
= 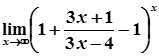 =
= 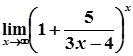 =
=
= 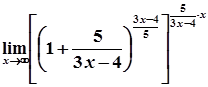 =
= 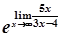 =
= 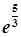 ;
;
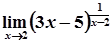 =
= 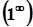 =
= 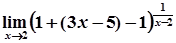 =
= 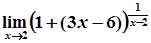 =
=
= 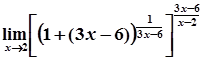 =
= 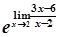 =
= 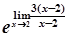 =
= 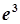 .
.
ПОХІДНІ
Похідні основних Похідні складених
Елементарних функцій елементарних функцій
1. 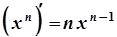 1а.
1а. 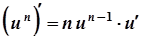
2. 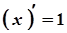
3. 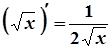 3а.
3а. 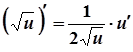
4. 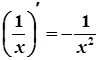 4а.
4а. 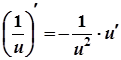
5. 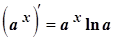 5а.
5а. 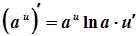
6. 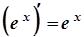 6а.
6а. 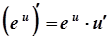
7. 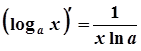 7а.
7а. 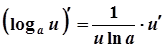
8. 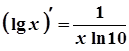 8а.
8а. 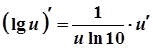
9. 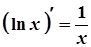 9а.
9а. 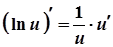
10. 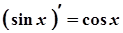 10а.
10а. 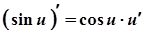
11. 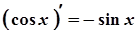 11а.
11а. 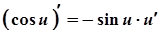
12. 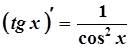 12а.
12а. 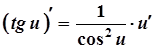
13. 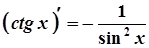 13а.
13а. 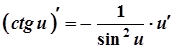
14. 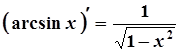 14а.
14а. 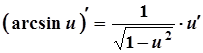
15. 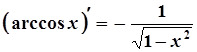 15а.
15а. 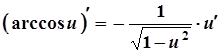
16. 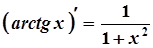 16а.
16а. 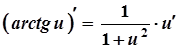
17. 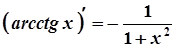 17а.
17а. 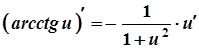
ПРАВИЛА ДИФЕРЕНЦІЮВАННЯ
1. 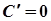
2. 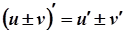
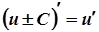
3. 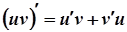
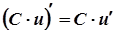
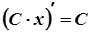
4. 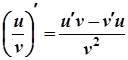
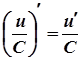
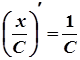
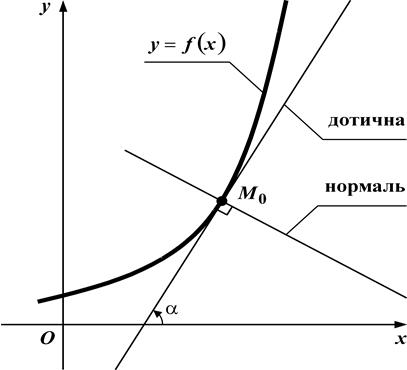
ДОТИЧНА І НОРМАЛЬ
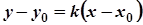 - рівняння прямої через т.
- рівняння прямої через т. 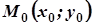 ;
;
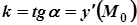 - геометричний зміст похідної;
- геометричний зміст похідної;
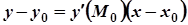 - рівняння дотичної;
- рівняння дотичної;
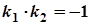 - умова перпендикулярності прямих;
- умова перпендикулярності прямих;
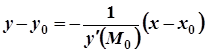 - рівняння нормалі.
- рівняння нормалі.
Дотична і нормаль до даної лінії в заданій точці – це є прямі, що проходить через точку дотику 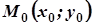 .
.
Геометричний зміст похідної в даній точці 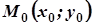 : значення похідної в даній точці
: значення похідної в даній точці 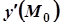 є тангенс кута
є тангенс кута 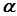 , під яким дотичне до кривої в точці
, під яким дотичне до кривої в точці 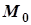 перетинає вісь
перетинає вісь 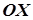 . Нормаль перпендикулярна до дотичної в точці дотику
. Нормаль перпендикулярна до дотичної в точці дотику 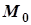 . Тому слід використати умову перпендикулярності двох прямих:
. Тому слід використати умову перпендикулярності двох прямих: 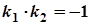 .
.
ЕКСТРЕМУМ ФУНКЦІЇ
Для дослідження функції і побудови її графіка студент повинен добре знати, що при зростанні функції - 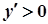 , при спаданні -
, при спаданні - 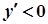 і розуміти різницю між необхідною та достатньою умовами існування екстремуму функції, а також необхідною і достатньою умовами існування точок перегину.
і розуміти різницю між необхідною та достатньою умовами існування екстремуму функції, а також необхідною і достатньою умовами існування точок перегину.
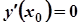 або не існує – необхідна умова існування екстремуму;
або не існує – необхідна умова існування екстремуму;
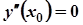 або не існує – необхідна умова існування точок перегину.
або не існує – необхідна умова існування точок перегину.
Із цих умов знаходяться критичні точки.
Достатня умова для існування екстремуму в т. 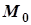 або точки перегину – зміна знака відповідно до першої і другої похідної при переході через критичну точку.
або точки перегину – зміна знака відповідно до першої і другої похідної при переході через критичну точку.
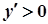 – функція зростає ↗;
– функція зростає ↗; 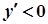 – функція спадає ↘;
– функція спадає ↘;
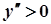 – функція вгнута
– функція вгнута 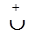 ;
; 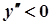 – функція опукла
– функція опукла 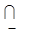 .
.
