Нахождение интервала и радиуса сходимости ряда

Разыскание интервала сходимости (абсолютной) ряда (1) может быть проведено следующим образом:

Можно исследовать ряд, составленный из модулей членов данного ряда: (*)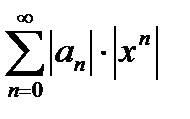

К ряду (*), члены которого положительны, применим признак Даламбера.

Интервалы сходимости рядов (1) и (*) совпадают (за исключением, быть может, их концов).

Допустим, что мы сумеем найти

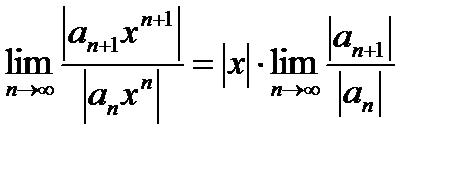
Этот предел будет содержать множитель 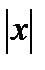, или некоторую степень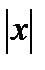

Для тех значений 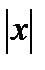, при которых этот предел 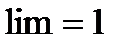, ряд сходится.

Значение 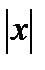, при котором 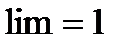, и будет являться радиусом сходимости ряда.

Если найденный 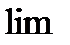при любом 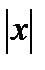равен нулю, то это означает, что ряд сходится всюду и .

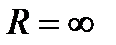Если же 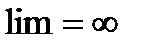, то ряд расходится при всяком 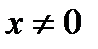, поэтому R=0.

Таким образом, для нахождения интервала сходимости (и радиуса) можно использовать признак Даламбера для абсолютной сходимости.

Аналогичным образом можно использовать признак Коши.

Для разыскания области сходимости ряда дополняют нахождение интервала сходимости исследованием поведения ряда на концах этого интервала.

Рассмотрим несколько примеров

Пример 6.2.27. Найти область сходимости и радиус сходимости ряда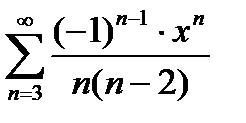

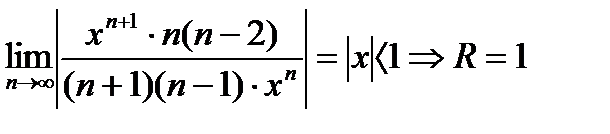
при х=1: 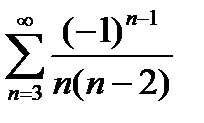- сходится по признаку Лейбница

при х=-1: 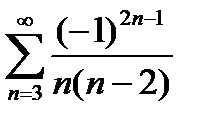=(все члены ряда отрицательны, поэтому можно записать)= = 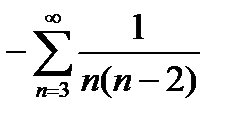; сравним ряд 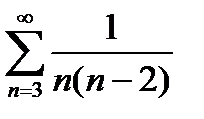с рядом 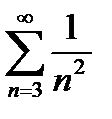: 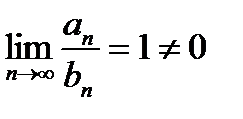. Следовательно, при х=-1 ряд сходится.

Ответ: область сходимости ряда 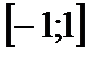; R=1 (ряд в этом промежутке сходится абсолютно).

Пример 6.2.28. Найти интервал сходимости ряда 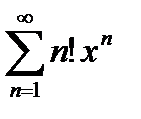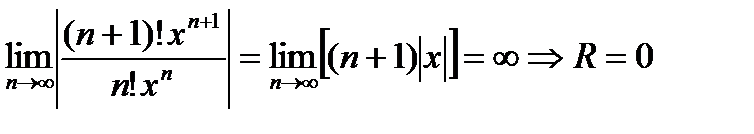- ряд расходится ÞR=0; ряд сходится только в т. х=0

Пример 6.2.29.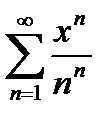

Применим признак Коши для абсолютной сходимости: 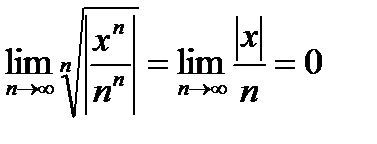- ряд сходится для всех х. Отсюда R= 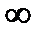и область сходимости ряда .

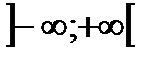Для степенных рядов вида 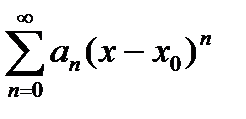все сказанное выше остается в силе с той только разницей, что теперь центр интервала сходимости будет не в т. х=0, а в точке х=х₀.

Интервал сходимости: .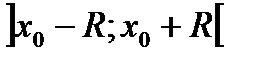

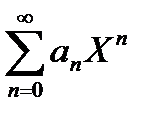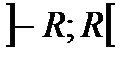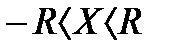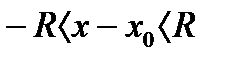Д-но, заменим х-х₀=Х, получим ряд Пусть этот ряд сходится в интервале , т. е. Û или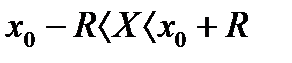

Пример 6.2.30. Определить радиус и область сходимости ряда 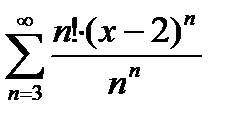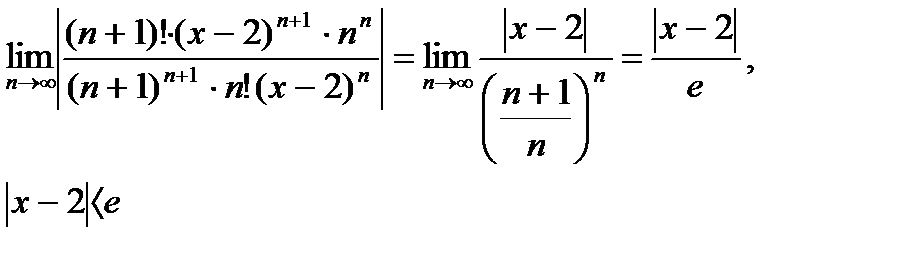, R=e;

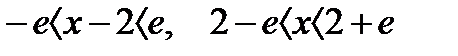
при х=2-e: 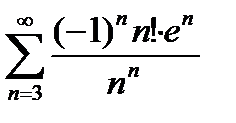- этот ряд расходится, т. к. его члены не убывают ( )

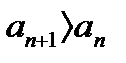при х=2+e: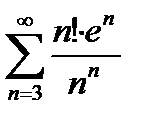

Воспользуемся признаком Даламбера (без предельного перехода), чтобы выяснить поведение этого ряда:

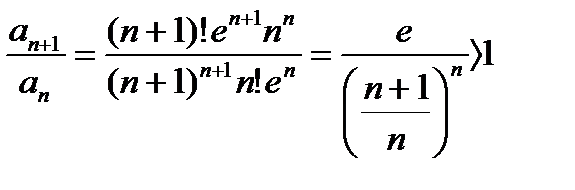- ряд расходится.

Ответ: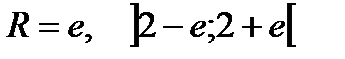

Пусть функция 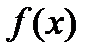бесконечно дифференцируема в некоторой окрестности точки х=х₀.

Если функция является суммой степенного ряда в каком-либо промежутке, то говорят, что в этом промежутке функция разлагается в степенной ряд.

В качестве промежутка обычно рассматривают некоторую окрестность т. х₀.

Допустим, что функция 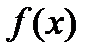разлагается в степенной ряд по степеням разности х-х₀ в некотором интервале, содержащем данную т. х₀:

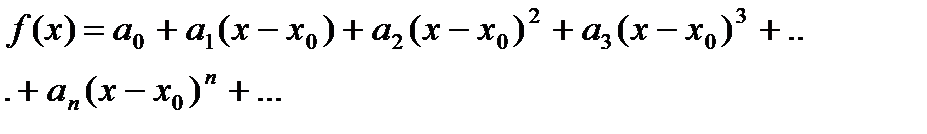
где 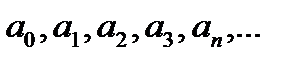- пока неопределенные коэффициенты.

Пользуясь свойством дифференцируемости степенных рядов, найдем эти коэффициенты по значениям функции 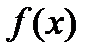и ее производных в т. х₀.

Имеем:

…

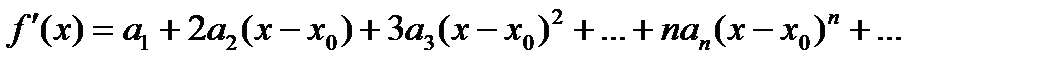
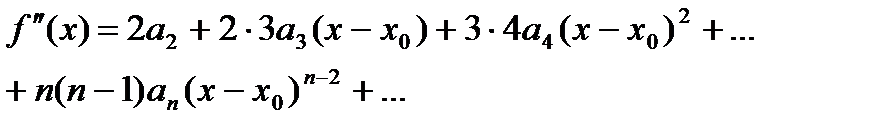
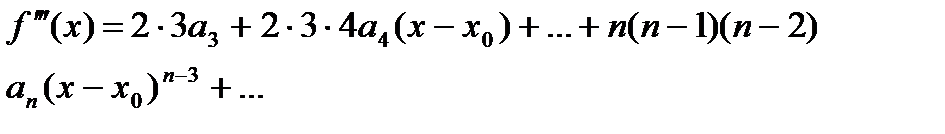
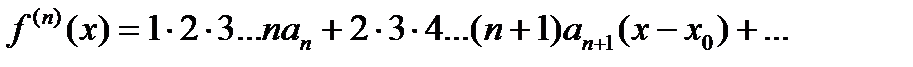(2)

Полагая , что х=х₀, получим:

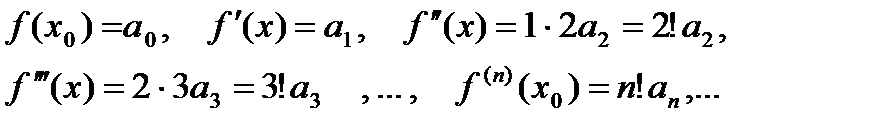
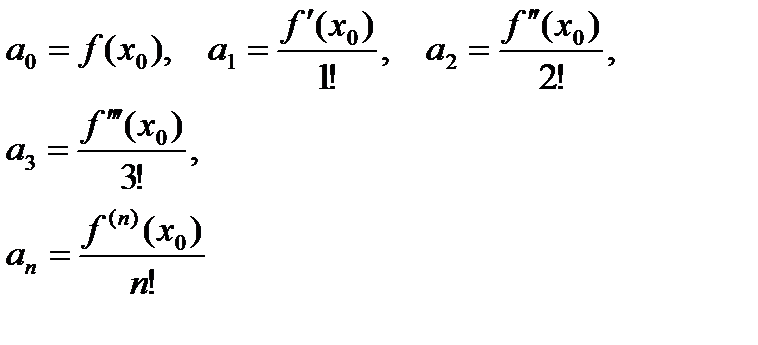(6.2.9.)

Таким образом, коэффициенты степенного ряда, суммой которого в соответствующем интервале является функция 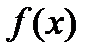, однозначно определяются с помощью формулы (6.2.9.: 1) функцией 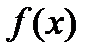и 2) точкой х₀ , так что представление функции 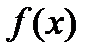степенным рядом в данном интервале (когда оно возможно) единственно.

Определение 6.2.10. Степенной ряд с коэффициентами, вычисленными по формулам (3), т. е. ряд вида

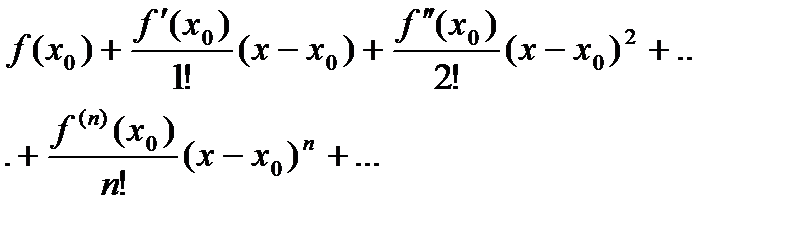
называется рядом Тейлора функции 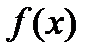, записанным по степеням разности х-х₀, или , иначе говоря, в окрестности т. х₀.

Если х₀=0, то ряд Тейлора принимает вид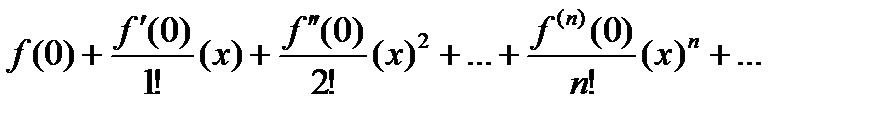

Этот частный случай ряда Тейлора называется рядом Маклорена.