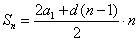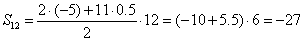МАША) Арифметические прогрессии

Числовая последовательность, каждый член которой, начиная со второго, равен предыдущему, сложенному с постоянным для этой последовательности числом d ,называется арифметической прогрессией. Число d называется разностью прогрессии. Любой член арифметической прогрессии вычисляется по формуле:

a_n = a₁ + d (n – 1) .

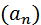• Если , то - возрастающая
• Если , то 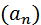- убывающая
• Если 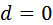, то 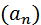- постоянна

Формула суммы n первых членов арифметической прогрессии:

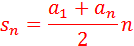
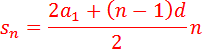
Определение арифметической прогрессии	an+1 = an + d
Разность арифметической прогрессии	d = an+1 - an
Формула n-го члена арифметической прогрессии	an = a1+ d · (n - 1)
Сумма n первых членов арифметической прогрессии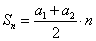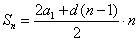

Последовательность 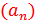является арифметической прогрессией тогда и только тогда, когда любой ее член, начиная со второго, является средним арифметическим предшествующего и последующего членов, то есть .

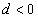Свойства:

1) Член арифметической прогрессии с номером 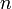может быть найден по формуле

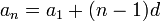, где 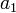— первый член прогрессии, 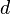— ее разность.

2) Характеристической свойство (признак) арифметической прогрессии: каждый член арифметической прогрессии, начиная со второго, есть среднее арифметическое соседних с ним членов

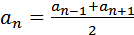. Где n 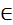N, n≥2

3) Если a1, a2, ..., an, ... - арифметическая прогрессия и k + n = m + p (k,n,m,p 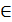 N), то

ak + an = am + ap.

Сумма Sn первых n членов арифметической прогрессии равна

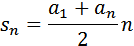4) Каждый член арифметической прогрессии, начиная со второго, есть среднее арифметическое соседних с ним членов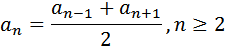

(АРИНА) Арифметические прогрессии высших порядков

Арифметической прогрессией 2-го порядка называется такая последовательность чисел, что последовательность их разностей сама образует простую арифметическую прогрессию. Примером может служить последовательность квадратов натуральных чисел:

0, 1, 4, 9, 16, 25, 36…,

разности, которых образуют простую арифметическую прогрессию с разностью 2:

1, 3, 5, 7, 9, 11…

Аналогично определяются и прогрессии более высоких порядков. В частности, последовательность n-ных степеней образует арифметическую прогрессию n-го порядка.

Примеры:

ü Натуральный ряд 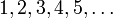— это арифметическая прогрессия, в которой первый член 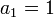, а разность .

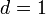ü 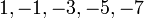— первые 5 членов арифметической прогрессии, в которо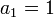й и .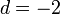

ü Если все элементы некоторой последовательности равны между собой и равны некоторому числу 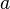, то это есть арифметическая прогрессия, в которо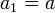й и 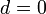. В частности, 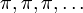есть арифметическая прогрессия с разностью .

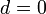ü Сумма первых 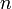натуральных чисел выражается формулой

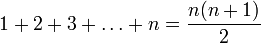
1) Найти сумму двенадцати первых членов арифметической прогрессии, если: а₁ = -5, d = 0,5

Решение: