Расчет токов и напряжений в симметричных трехфазных цепях
Методические указания
При подготовке к занятию необходимо ознакомиться с соответствующими разделами теории по учебной литературе: [1, c.283–287]; [3, с.169–178].
Ответьте на вопросы:
1. Изобразите электрическую цепь, в которой источник трехфазного напряжения, собранный по схеме звезды, соединен с нагрузкой, также собранной по схеме звезды. Кроме того, в цепи имеется еще нулевой провод, соединяющий их нейтрали, причем его сопротивление не равно нулю.
Укажите на схеме условные положительные направления токов в трехфазной линии, токов в фазах звезды и в нулевом проводе, фазные и линейные напряжения у источника и нагрузки, а также напряжения в нулевом проводе. Как линейные напряжения выражаются через фазные напряжения?
2. Изобразите электрическую цепь нагрузки, собранной по схеме треугольника, питающуюся от трехфазной системы линейных напряжений. Так же, как в п.1, укажите условные положительные направления токов и напряжений.
Как при соединении треугольником линейные токи выражаются через фазные?
3. Охарактеризуйте трехфазный симметричный источник напряжения. Приведите схемы его соединений звездой, треугольником. Не кажется ли вам, что при соединении треугольником в образовавшемся замкнутом контуре будет циркулировать огромный ток короткого замыкания?
4. Какие условия следует выполнить, чтобы трехфазная цепь была симметричной?
5. Если трехфазная симметричная цепь собрана по схеме звезды, в каком числовом соотношении находятся действующие значения линейных и фазных напряжений? А как они соотносятся по своим начальным фазам?
6. То же – о линейных и фазных токах в треугольнике.
7. Если симметричная цепь соединена по схеме «звезда-звезда», то чему равно напряжение между нейтралями источника напряжения и нагрузки? Зависит ли это от того, имеется четвертый провод или его нет?
8. Дайте толкование положению о том, что расчет токов и напряжений в симметричной трехфазной цепи сводится к расчету этих величин в одной фазе. Если в результате расчета найден ток фазы А: 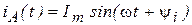 . Сформулируйте выражения
. Сформулируйте выражения 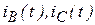 .
.
9. Нагрузка соединена по схеме звезды: 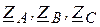 . Найдите три сопротивления:
. Найдите три сопротивления: 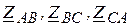 , с помощью которых можно образовать соединение треугольником, эквивалентным заданной звезде. Выполните такую же операцию в противоположном направлении: от треугольника к звезде.
, с помощью которых можно образовать соединение треугольником, эквивалентным заданной звезде. Выполните такую же операцию в противоположном направлении: от треугольника к звезде.
Если трехфазная схема симметрична, то 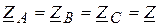
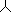 ,
, 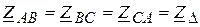 . Найдите связь между
. Найдите связь между 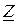
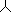 и
и 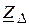 , используемую при взаимных эквивалентных переходах от одной схемы к другой в симметричном случае.
, используемую при взаимных эквивалентных переходах от одной схемы к другой в симметричном случае.
10. К системе трех линейных проводов подключены две нагрузки: одна – звездой ( 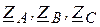 ), другая треугольником (
), другая треугольником ( 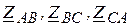 ). Предложите порядок преобразований схемы с тем, чтобы в конечном итоге получить схему нагрузки в форме эквивалентной звезды.
). Предложите порядок преобразований схемы с тем, чтобы в конечном итоге получить схему нагрузки в форме эквивалентной звезды.
З а д а ч а 10.1
В симметричной трехфазной цепи определите значения неизвестных величин (табл.10.1).
Таблица 10.1
Исходные данные к задаче 10.1
| Вариант | Схема | Uл, В | Uф, В | Iл, A | Iф, A | Вариант | Схема | Uл, В | Uф, В | Iл, A | Iф, A |
 | ? | ? |  | ? | ? | ||||||
 | ? | ? |  | ? | ? | ||||||
 | ? | ? |  | ? | ? | ||||||
 | ? | ? |  | ? | ? | ||||||
 | ? | ? |  | ? | ? | ||||||
 | ? | ? |  | ? | ? | ||||||
 | ? | ? |  | ? | ? | ||||||
 | ? | ? |  | ? | ? | ||||||
 | ? | ? |  | ? | ? | ||||||
 | ? | ? |  | ? | ? | ||||||
 | ? | ? |  | ? | ? | ||||||
 | ? | ? |  | ? | ? | ||||||
 | ? | ? |  | ? | ? | ||||||
 | ? | ? |  | ? | ? | ||||||
 | ? | ? |  | ? | ? |
З а д а ч а 10.2
В симметричных трехфазных цепях, схемы которых представлены на рис.10.1, определите мгновенные и комплексные действующие значения указанных в табл.10.2 величин. Постройте векторные диаграммы токов и напряжений.
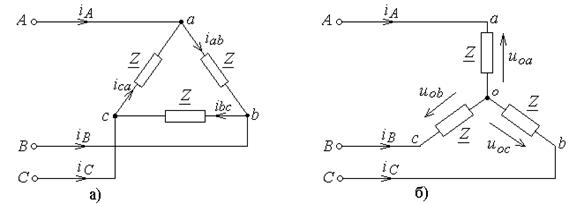
Рис.10.1. Соединение трехфазной нагрузки треугольником (а) и звездой (б)
Таблица 10.2
Исходные данные к задаче 10.2
| Вариант | Схема из рис.10.1 | Дано | Определить | Вариант | Схема из рис.10.1 | Дано | Определить |
| а б | 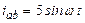 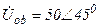 | 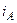 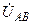 | а б | 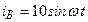 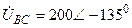 | 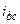 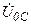 | ||
| а б | 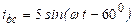 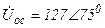 | 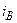 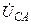 | а б | 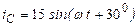 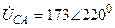 | 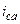 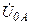 | ||
| а б | 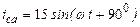 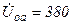 | 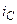 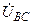 | а б | 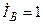 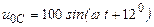 | 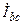 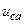 | ||
| а б | 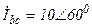 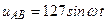 | 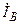 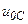 | а б | 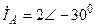 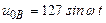 | 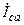 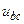 | ||
| а б | 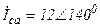 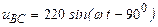 | 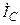 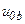 | а б | 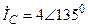 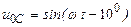 | 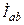 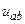 | ||
| а б | 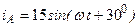 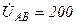 | 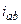 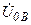 | а б | 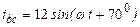 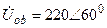 | 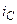 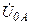 | ||
| а б | 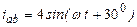 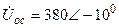 | 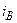 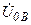 | а б | 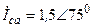 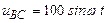 | 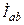 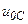 | ||
| а б | 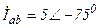 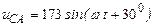 | 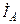 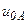 | а б | 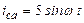 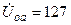 | 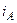 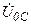 |
Окончание табл.10.2
| Вариант | Схема из рис.10.1 | Дано | Определить | Вариант | Схема из рис.10.1 | Дано | Определить |
| а б | 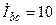 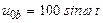 | 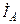 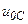 | а б | 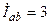 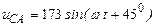 | 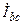 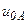 | ||
| а б | 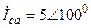 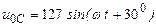 | 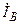 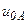 | а б | 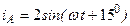 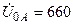 | 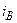 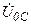 | ||
| а б | 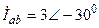 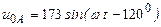 | 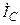 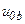 | а б | 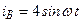 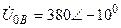 | 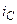 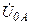 | ||
| а б | 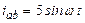 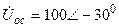 | 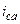 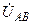 | а б | 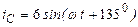 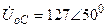 | 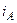 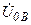 | ||
| а б | 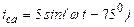 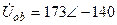 | 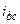 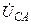 | а б | 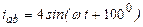 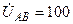 | 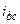 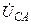 | ||
| а б | 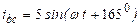 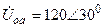 | 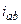 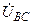 | а б | 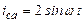 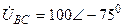 | 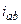 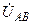 | ||
| а б | 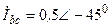 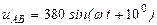 | 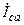 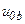 | а б | 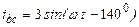 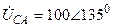 | 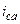 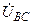 |
З а д а ч а 10.3
В симметричной трехфазной цепи (рис.10.2,а), рассчитайте фазные и линейные токи и напряжения. Исходные данные приведены в табл.10.3.
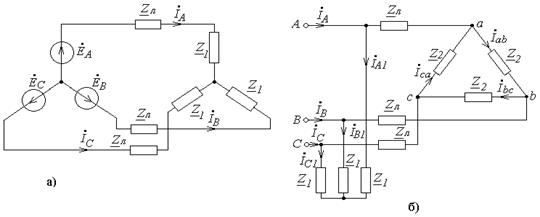
Рис.10.2. Схемы к задачам 10.3, 10.4
З а д а ч а 10.4
Рассчитайте токи, указанные на схеме (рис.10.2,б), если соответствующая цепь симметрична, значения 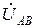 заданы численно равными
заданы численно равными 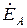 из табл.10.3, величины
из табл.10.3, величины 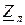 и
и 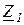 указаны там же, а
указаны там же, а 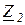 для всех вариантов одинаково и равно 150 Ом.
для всех вариантов одинаково и равно 150 Ом.
Таблица 10.3
Исходные данные к задачам 10.3, 10.4
| Вариант | 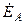 , В , В | 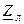 , Ом , Ом | 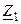 , Ом , Ом | Вариант | 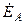 , В , В | 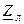 , Ом , Ом | 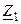 , Ом , Ом |
| 220Ð300 | j 20 | 20–j 40 | 220Ð500 | –j 20 | 50–j 20 | ||
| 127Ð600 | j 50 | j 50 | 173Ð700 | j 50 | 50+j 50 | ||
| 173Ð100 | –j 10 | j 30 | 100 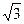 | j 80 | 20–j 10 | ||
| 380Ð600 | j 100 | –j 150 | 380Ð300 | –j 150 | |||
| 220Ð100 | j 100 | j 50 | 220Ð900 | –j 50 | 100+j 200 | ||
| 137Ð200 | j 60 | j 20 | 660Ð100 | j 70 | 40+j 20 | ||
127 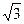 | j 20 | j 70 | 127 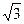 | 40+j 60 | |||
| 173Ð400 | j 20 | 40+j 70 | 380Ð200 | j 70 | 40+j 20 | ||
| 380Ð500 | j 40 | 10+j 10 | 220Ð450 | 40+j 100 | |||
| 660Ð700 | –j 220 | j 150 | 173Ð300 | j 200 | |||
| 220Ð400 | j 70 | 50+j 30 | 660Ð600 | j 30 | 50+j 70 | ||
| 127Ð500 | j 30 | 20+j 10 | j 20 | 30+j 100 | |||
| 173Ð600 | –j 40 | 40+j 13 | 220Ð750 | j 40 | 60+j 150 | ||
127 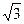 | j 50 | –j 100 | 380Ð900 | –j 100 | 50+j 20 | ||
| 380Ð450 | j 20 | 10+j 80 | 220Ð300 | 10–j 0 |
ЗАНЯТИЕ 11
