Теорема взаимности в теории излучения

Рассматриваем поля, которые зависят от времени по закону:

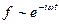
И рассмотрим уравнения Максвелла:

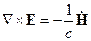
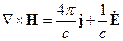
Если учитывать временную зависимость для Е и Н и если ввести 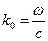, то получим:

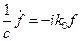
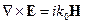
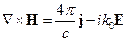
Теорема взаимности рассматривает две группы источников и полей. Источником является ток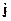

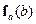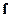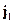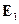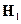- поле , создаваемое источником «а» в области «b». Таким образом, источник порождает поля и , а 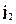порождает поля 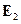и .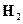

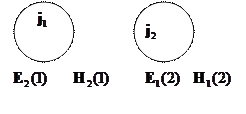Перепишем уравнения Максвелла для 1 и для 2 источников:

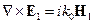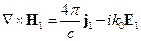
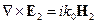и

и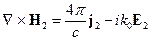

Для первого источника, умножим левое и правое уравнение скалярно на 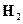и 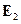соответственно, и к первому прибавим второе:

(*)

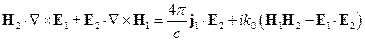
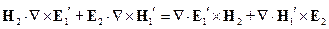
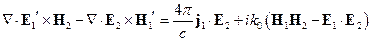Для второго источника:

(**)

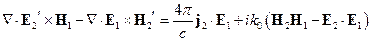Из (*) вычтем (**):

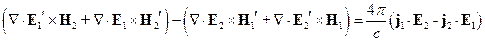
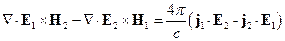
Проинтегрировав обе части этого уравнения по объему и, используя теорему Остроградского-Гаусса, получим:

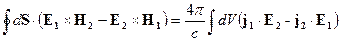
Здесь предполагается, что поле на бесконечности обращается в нуль, это обращение происходит за счет поглощения волны, тогда:

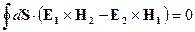
и значит:

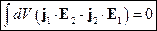- теорема взаимности для излучения

Этот интеграл берется по областям, где есть источники. Области источников ограничивают области интегрирования. Там, где нет источников, этот интеграл равен нулю.

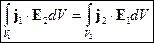
То есть перемена местами источников и полей не меняет результата.

Предполагая, что поле достаточно медленно меняется в достаточно малой области локализации источников, можно поле вынести за знак интеграла, тогда:

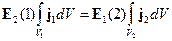
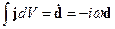
Тогда:

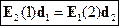- теорема взаимности для дипольного излучения.

Используем приближение линейного тока:

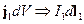
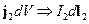
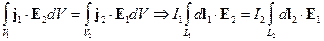
Если контуры замкнутые, то 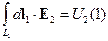- падение напряжения на 1-м контуре за счет излучения 2-го источника. Обозначим 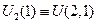и 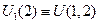, тогда:

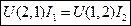
Мы получили теорему взаимности для контуров, реагирующих на излучение.

Задачи по курсу «Электродинамика сплошных сред»