Двойной интеграл в прямоугольных координатах
Пусть функция f(x,y) определена и непрерывна в ограниченной замкнутой области Д плоскости хОу. Разобьем область Д произвольным образом на n элементарных областей, имеющих площади 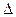 S1 ,
S1 , 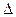 S2 , ... ,
S2 , ... , 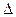 Sn и диаметры d1,d2, ..., dn (диаметром называется наибольшее из расстояний между двумя точками границы этой области). Выберем в каждой элементарной области произвольную точку Pi(xi, yi) и составим следующую сумму:
Sn и диаметры d1,d2, ..., dn (диаметром называется наибольшее из расстояний между двумя точками границы этой области). Выберем в каждой элементарной области произвольную точку Pi(xi, yi) и составим следующую сумму:
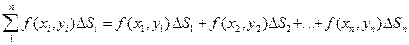 .
.
Такая сумма называется интегральной суммой.
Определение:
Предел интегральной суммы при условии, что число элементарных областей n ®  и наибольший диаметр max dk ® 0, называется двойным интегралом от функции f(x, y) по области Д, если этот предел существует и не зависит :
и наибольший диаметр max dk ® 0, называется двойным интегралом от функции f(x, y) по области Д, если этот предел существует и не зависит :
1) ни от способа разбиения области Д на элементарные области;
2) ни от способа выбора в них точек Рi
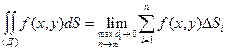 .
.
Если f(x, y) > 0 в области Д, то двойной интеграл 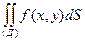 равен объему цилиндрического тела, ограниченного сверху поверхностью z = f(x, y), сбоку - образующими параллельные оси Оz, а снизу - областью Д (лежащей на плоскости хОу).
равен объему цилиндрического тела, ограниченного сверху поверхностью z = f(x, y), сбоку - образующими параллельные оси Оz, а снизу - областью Д (лежащей на плоскости хОу).
Свойства двойного интеграла аналогичны свойствам определенного интеграла.
ВЫЧИСЛЕНИЕ ДВОЙНОГО ИНТЕГРАЛА
Существуют два основных вида области интегрирования:
1.Область интегрирования Д ограничена слева и справа прямыми х = а,
х = в (а < в), а снизу и сверху - непрерывными кривыми у = j1(х) и у =j2(х)
(j1(х) £ j2(х)), каждая из которых пересекается прямой, параллельной оси Оу, только в одной точке (рис. 1).
| |||||||
 | |||||||
 | |||||||
| |||||||




 |
| ||||||
| |||||||
 | |||||||
Рис. 1
 | |||
| |||
Рис. 2
Вычисление двойного интеграла сводится к двукратному интегрированию
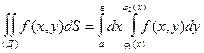 .
.
Интеграл 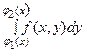 называется внутренним. В нем х считается постоянной. Этот интеграл вычисляется в первую очередь. А потом вычисляется внешний интеграл по переменной х.
называется внутренним. В нем х считается постоянной. Этот интеграл вычисляется в первую очередь. А потом вычисляется внешний интеграл по переменной х.
Для того, чтобы поставить пределы внутреннего интеграла, надо посмотреть на изменение у вдоль вектора 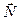 от точки входа вектора в область Д (нижний предел) до точки выхода вектора из области Д (верхний предел). Пределы внешнего интеграла всегда постоянны и показывают пределы изменения переменной х.
от точки входа вектора в область Д (нижний предел) до точки выхода вектора из области Д (верхний предел). Пределы внешнего интеграла всегда постоянны и показывают пределы изменения переменной х.
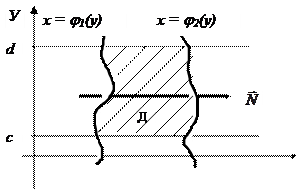
2. Пусть область интегрирования Д ограничена снизу и сверху прямыми
у = с, у = d (с < d) , а слева и справа - непрерывными кривыми х = Y1(у), х = Y2(у) (Y1 (у) £ Y1 (у)), каждая из которых пересекается горизонтальной прямой только в одной точке (рис. 2).
Тогда двойной интеграл по такой области вычисляется по формуле
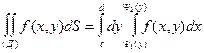 ,
,
причем сначала вычисляется внутренний интеграл, 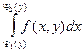 , в котором у считается постоянной.
, в котором у считается постоянной.
ЗАДАЧА № 13
Вычислить повторные интегралы
1.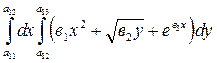 ;2.
;2.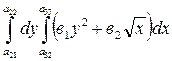 .
.
|
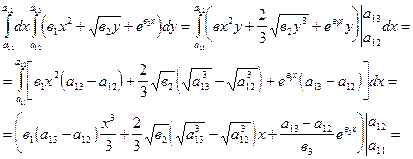
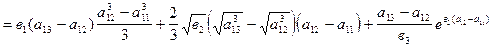 .
.
|
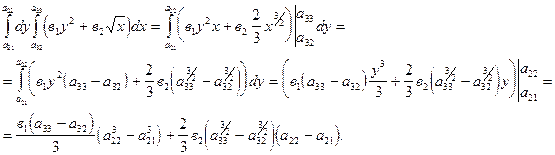
ЗАДАЧА № 14
Вычислить следующие двойные интегралы по области Д, ограниченные линиями
1.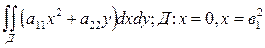 ; 2.
; 2.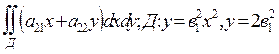 .
.
1. 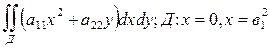 ;
; 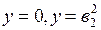 .
.
 | |||||
 | |||||
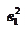 | |||||
|
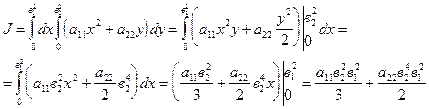
2. 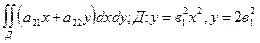 ;
; 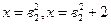 ;
;
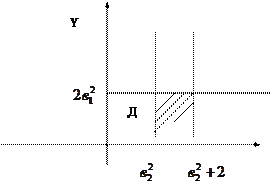 | |||
| |||

|
|
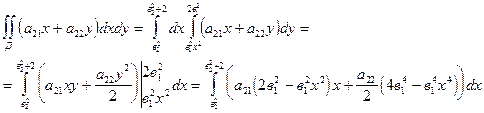
= 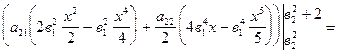
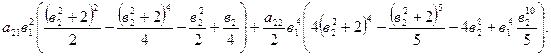
КОНТРОЛЬНАЯ РАБОТА №4
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
