Контроль по количественному признаку
При контроле по количественному признаку измеряют числовые значения контролируемого параметра единиц продукции, вычисляют выборочное среднее арифметическое значение и оценивают его отклонение от одной или одновременно двух заданных границ. Цена деления шкалы измерительного средства не должна превышать значения среднего квадратического отклонения контролируемого параметра (если это значение неизвестно, можно использовать его ожидаемое значение).
Преимущество контроля по количественному признаку – малые объёмы выборок ( в 10-20 раз меньше, чем при контроле альтернативному признаку). Это связано с тем, что каждая выборка даёт объём информации, состоящий из n чисел. При контроле по альтернативному признаку объём информации состоит из количества дефектных единиц продукции в выборке (одного числа). Недостатки метода- измерения дороже и планы контроля сложнее.
Обычно предполагают, что количественный признак (параметр) единицы продукции имеет нормальное распределение с параметрами а и 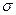 :
:
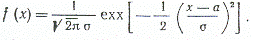
Могут использоваться и другие распределения.
Вероятность q изготовления дефективного изделия полностью определяется границами допуска ( 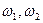 ) ,математическим ожиданием a и средним квадратическим отклонением
) ,математическим ожиданием a и средним квадратическим отклонением 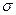 параметра изделия.
параметра изделия.
Задача выборочного контроля в данном случае состоит в том, чтобы по результатам анализа выборочных характеристик (среднего арифметического значения 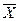 и выборочного среднего квадратического отклонения
и выборочного среднего квадратического отклонения 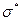 ) сделать утверждения относительно характеристик партии, а и
) сделать утверждения относительно характеристик партии, а и 
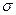 с тем, чтобы принять или забраковать партию.
с тем, чтобы принять или забраковать партию.
В дальнейшем рассмотрим схему проведения количественного контроля по методу Неймана- Пирсона. Предположим что партия забраковывается, когда процент брака равен 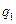 и принимается когда процент брака равен
и принимается когда процент брака равен 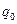 .
.
Таким образом требуется различить две гипотезы:
гипотеза 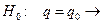 приемка партии;
приемка партии;
гипотеза 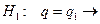 браковка партии.
браковка партии.
От исходных гипотез перейдем к гипотезам различения математических ожиданий:
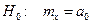 ;
; 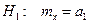 .
.
При решении задачи предположим, что отказ наступает при выполнении условия 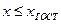 .
.
Тогда, в предположении нормального закона распределения, вероятность отказа будет равна
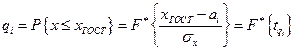 ,
,
где 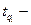 аргумент функции нормированного нормального распределения, соответствующий вероятности отказа
аргумент функции нормированного нормального распределения, соответствующий вероятности отказа 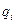 . Приравнивая аргументы, получим
. Приравнивая аргументы, получим

Отсюда найдем 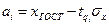 .
.
Для определения приемочного уровня 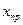 и числа испытаний n воспользуемся соотношениями (3.7) и (3.8) . Учитывая, что
и числа испытаний n воспользуемся соотношениями (3.7) и (3.8) . Учитывая, что 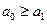 , получим
, получим
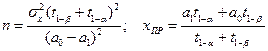 .
.
Пример. Рассмотрим задачу различения двух гипотез :
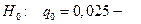 приемка партии,
приемка партии,
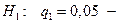 браковка партии.
браковка партии.
При задании исходных данных воспользуемся результатами статистической обработки механических свойств листов из сплава АМг6Н [12]:
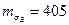 МПа – математическое ожидание предела прочности,
МПа – математическое ожидание предела прочности,
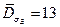 МПа - среднее квадратическое отклонение предела прочности,
МПа - среднее квадратическое отклонение предела прочности,
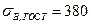 МПа - предел прочности материала по ГОСТу,
МПа - предел прочности материала по ГОСТу,
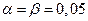 - риски поставщика и заказчика.
- риски поставщика и заказчика.
Результаты расчетов представлены ниже:
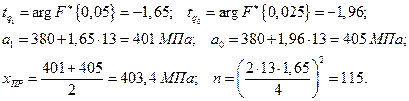
Заметим, что для партии листов с принятыми характеристиками, вероятность брака будет равна