Способ представления гармонических колебаний

Метод двух узлов

Для цепей, имеющих только два узла 1 и 2.

План анализа:

Произвольно выбрать направления всех токов в ветвях на исходной схеме.

Вычислить узловое напряжение, направленное от узла 1 к узлу 2.

(6) МЭГ

Если в электрической цепи необходимо определить ток только в одной из ветвей, то используют метод эквивалентного генератора. Метод основан на теореме о двухполюснике, в соответствии с которой любой активный двухполюсник можно представить реальным источником ЭДС. Применение данного метода особенно эффективно, когда требуется определить значения тока в некоторой ветви для различных значений сопротивления в этой ветви в то время, как в остальной схеме сопротивления, а также ЭДС и токи источников постоянны. Теорема об активном двухполюснике формулируется следующим образом: если активную цепь, к которой присоединена некоторая ветвь, заменить источником с ЭДС, равной напряжению на зажимах разомкнутой ветви, и сопротивлением, равным входному сопротивлению активной цепи, то ток в этой ветви не изменится.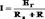

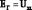(Холостой ход) (Режим короткого замыкания: )

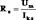(7) Баланс мощности

Одной из наиболее общих теорем теории электрических цепей является теорема Телледжена Из теоремы Телледжена вытекает ряд следствий, важнейшим из которых является баланс мощности.Действительно, произведениеu_k i_k представляет собой мгновенную мощностьр_k k-й ветви, поэтому сумма мощностей всех ветвей цепи равняется нулю. Если выделить ветви с независимыми источниками, то баланс мощности можно сформулировать следующим образом: сумма мощностей, отдаваемых независимыми источниками, равняется сумме мощностей, потребляемых остальными ветвями электрической цепи.

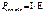
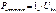
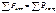
Гармонические токи, напряжения, ЭДС.

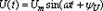
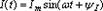
Гармонические токи, и напряжения - это такие токи и напряжения, которые изменяются во времени по гармоническим законам 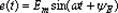где и(ft), i(t), e(t) - мгновенные значения напряжения, тока и ЭДС; Um,Im,Em - амплитудные значения, т.е. наибольшие значения гармонической функции; 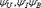-начальная фаза напряжения,тока и ЭДС. w-круговая частота,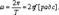

f-частота ,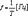

Способ представления гармонических колебаний.

Гармоническое колебание — явление периодического изменения какой-либо величины, при котором зависимость от аргумента имеет характер функции синуса или косинуса. Например, гармонически колеблется величина, изменяющаяся во времени следующим образом: x(t) = Asin(ωt + φ) x(t) = Acos(ωt + φ), где х — значение изменяющейся величины, t — время, остальные параметры - постоянные: А — амплитуда колебаний, ω — циклическая частота колебаний, (ωt + φ) — полная фаза колебаний, 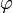— начальная фаза колебаний. Гармонические колебания можно представить несколькими способами:

аналитический:

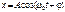графический:

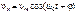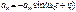геометрический, с помощью вектора амплитуды (метод векторных диаграмм).

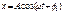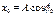(11) Гармонические колебания в резистивных, индуктивных и емкостных элементах

Гармонические колебания в резистивных элементах

Пусть через пассивный резистор проходит гармонический ток i(t)=Im sin(wt+yi).

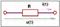
Принимая во внимание закон Ома для мгновенных значений найдем

u=R i=R Im sin(wt+yi)=Um sin(wt+yu),

т.е. j=yu–yi=0 т.к. yu=yi и Um=R Im.

Следовательно, напряжение и ток в данном случае имеют одинаковую начальную фазу, т.е. они совпадают по фазе

Амплитуды и соответственно действующие значения гармонических колебаний напряжения и тока в резистивном сопротивлении связаны законом Ома

Im=Um/R и I=U/R.

Вся энергия, поступающая в резистивный элемент, преобразуется в тепло. Мгновенная мощность равна

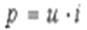
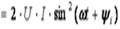
Гармонические колебания в индуктивных элементах

Мгновенное напряжение на индуктивном элементе изменяется по закону

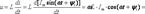
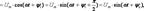
где yu=yi+p/2, j=yu-yi =yi -yi +p/2=p/2, Um=wL Im.

Следовательно, напряжение на индуктивности имеет форму гармонического колебания и опережает по фазе колебания тока на угол p/2 или, что то же, гармоническое колебание тока в индуктивности отстает по фазе от колебаний напряжения на угол p/2

Мгновенная мощность при этом изменяется во времени по закону

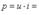
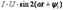
Амплитуды и соответствующие действующие значения напряжения и тока на индуктивности связаны соотношением, подобным закону Ома

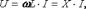
и где X=wL – индуктивное сопротивление, Ом.

Гармонические колебания в ёмкостных элементах

Мгновенное напряжение на ёмкости изменяется по закону при U0=0.

(12) Гармонические колебания в цепи при последовательном соединении R,L,C элементах

Рассмотрим процессы в цепи, содержащей последовательно соединенные R, L, C элементы в которых протекает ток.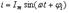

Определим общее сопротивление цепи. Поскольку элементы R, L и C соединены последовательно, то комплексное сопротивление цепи равно сумме комплексных сопротивлений

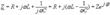
где Z и - модуль и фаза комплексного сопротивления.

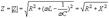
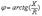
Ток , протекая по цепи , создает на ее элементах R, L и C падения напряжений UR, UL и UC, алгебраическая сумма которых равна приложенному к цепи напряжению, т.е.

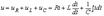
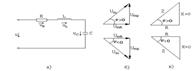
Цепь с последовательно соединенными R, L, C элементами (а) и треугольники напряжений (б) и сопротивлений (в).

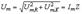
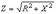
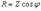
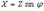
Формулы используются при расчетах цепей, состоящих из последовательно соединенных R, L,C элементов.

(13) Гармонические колебания в цепи при параллельном соединении R,L,C элементах

Пусть к цепи, содержащей параллельное соединение R, L, и C элементов , приложено напряжение

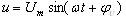
Общая комплексная проводимость цепи , состоящей из последовательно соединенных элементов R, L и C, равна сумме комплексных проводимостей ее элементов G, BL и BC.

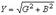
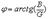
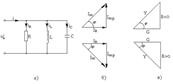
Цепь с параллельно соединенными R, L, C элементами (а) и треугольники токов (б) и проводимостей (в).

На основании треугольников токов и проводимостей можно записать следующие формулы:

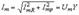
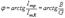
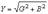
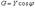
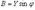
(14) Символический метод расчета цепей в разветвленных электрических цепях

Анализ электромагнитных процессов в электрических цепях переменного тока в общем случае возможен только с использованием представления токов, напряжений и параметров цепи комплексными числами. Это позволяет исключить тригонометрические функции из уравнений, описывающих электрическую цепь и сделать их линейными. Так как при этом все величины заменяются их изображениями или символами, то этот метод носит название символического.Последовательность операций в символическом методе в общем случае следующая:

1)преобразование всех величин и параметров электрической цепи в их изображения комплексными числами;

2)преобразование исходной электрической цепи в символическую схему замещения, где все величины и параметры представлены изображениями;

3)эквивалентные преобразования схемы замещения (если требуется);

4)определение искомых величин в области изображений;

5)преобразование искомых величин в оригиналы (если требуется).

Символическое изображение синусоидальных функций комплексными величинами

Любую гармоническую функцию 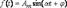можно изобразить в виде вектора а каждому вектору можно поставить в соответствие комплексное число

Существуют три формы записи комплексного числа

- показательная (А - модуль комплексного числа, j - его аргумент);

- тригонометрическая;

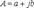- алгебраическая (а - вещественная часть, б – мнимая часть).

(15) Мощность в цепи синусоидального тока

Мгновенной мощностью называют произведение мгновенного напряжения на входе цепи на мгновенный ток.

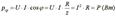
Среднее арифметическое значение мощности за период называют активной мощностью и обозначают буквой P. Эта мощность измеряется в ваттах и характеризует необратимое преобразование электрической энергии в другой вид энергии, например, в тепловую, световую и механическую энергию.

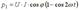- мгновенная мощность в активном сопротивлении;

- мгновенная мощность в реактивном элементе (в индуктивности или в емкости).

Максимальное или амплитудное значение мощности p2 называется реактивной мощностью

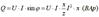
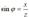
где x - реактивное сопротивление (индуктивное или емкостное).

Реактивная мощность, измеряемая в вольтамперах реактивных, расходуется на создание магнитного поля в индуктивности или электрического поля в емкости. Энергия, накопленная в емкости или в индуктивности, периодически возвращается источнику питания.

Полная мощность, измеряемая в вольтамперах, равна произведению действующих значений напряжения и тока:

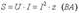
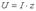
где z - полное сопротивление цепи.

Полная мощность характеризует предельные возможности источника энергии.

Возьмем треугольник сопротивлений и умножим его стороны на квадрат тока в цепи. Получим подобный треугольник мощностей

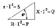
Из треугольника мощностей получим ряд формул:

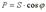
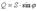
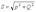
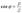
Активная мощность всегда положительна. Реактивная мощность в цепи, имеющей индуктивный характер, - положительна, а в цепи с емкостным характером - отрицательна.

(17) Топографические и векторные диаграммы

Совокупность радиус-векторов, изображающих синусоидально изменяющиеся ЭДС, напряжения, токи и т. д., называется векторной диаграммой. Векторные диаграммы наглядно иллюстрируют ход решения задачи. При точном построении векторов можно непосредственно из диаграммы определить амплитуды и фазы искомых величин.

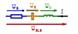
Векторная диаграмма для RLC-цепочки. (Стрелки в нижней части рисунка не являются векторами векторной диаграммы, а лишь показывают участки цепи, напряжения на которых соответствует векторам с таким же буквенным обозначением и цветом в верхней части рисунка, как раз и являющейся собственно векторной диаграммой).

Для наглядного определения величины и фазы напряжения между различными точками электрической цепи удобно использовать топографические диаграммы. Они представляют собой соединенные соответственно схеме электрической цепи точки на комплексной плоскости, отображающие их потенциалы.

(18) Комплексные входные и передаточные функции электрических цепей

С анализом работы линейных электрических цепей тесно связаны такие понятия, как входные и передаточные функции.

К входным функциям относят комплексное входное сопротивление линейной электрической цепи, определяемое как отношение напряжения и тока со стороны одноименных зажимов

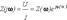и комплексная входная проводимость

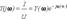
В этих формулах и – модули входного сопротивления и входной проводимости соответственно; 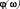– фазовый сдвиг между током и напряжением

Формально под передаточной функцией подразумевается комплексный переменный коэффициент, устанавливающий линейную алгебраическую зависимость между выходной величиной 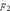(ток или напряжение в цепи) и входной величиной (ток или напряжение, подаваемые к входным зажимам). Так, если существует линейная зависимость

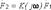, то величина определяется как передаточная функция цепи. Математически эта функция представляется, как правило, в виде рациональной дроби комплексной переменной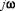

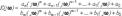
коэффициенты полиномов числителя и знаменателя которой определяются через параметры R, L и C самой цепи, т. е. являются вещественными положительными числами. На конкретной частоте передаточная функция есть комплексное число

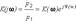где 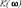ее модуль, определяющий отношение действующих или амплитудных значений выходного и входного сигналов, а 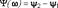аргумент, выражающий фазовый сдвиг между начальными фазами

(19) Явление взаимной индукции. ЭДС и напряжение взаимной индукции

Взаимоиндукция (взаимно индукция) — возникновение электродвижущей силы (ЭДС) в одном проводнике вследствие изменения силы тока в другом проводнике или вследствие изменения взаимного расположения проводников. Взаимоиндукция — частный случай более общего явления — электромагнитной индукции. При изменении тока в одном из проводников или при изменении взаимного расположения проводников происходит изменение магнитного потока через (воображаемую) поверхность, "натянутую" на контур второго, созданного магнитным полем, порожденным током в первом проводнике, что по закону электромагнитной индукции вызывает возникновение ЭДС во втором проводнике. Если второй проводник замкнут, то под действием ЭДС взаимоиндукции в нём образуется индуцированный ток. И наоборот, изменение тока во второй цепи вызовет появление ЭДС в первой. Направление тока, возникшего при взаимоиндукции, определяется по правилу Ленца. Явление взаимоиндукции широко используется для передачи энергии из одной электрической цепи в другую, для преобразования напряжения с помощью трансформатора.

Электродвижущая сила (ЭДС) — физическая величина, характеризующая работу сторонних (непотенциальных) сил в источниках постоянного или переменного тока. Величина ЭДС индукции в контуре определяется выражением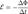

(20) Последовательное и параллельное соединение индуктивно связанных элементов