Расчет сложных электрических цепей постоянного тока методом контурных токов

КРАТКАЯ ТЕОРИЯ

Уравнения Кирхгофа позволяют рассчитать электрическую любую цепь, но при этом число решаемых уравнений может быть велико. Для сокращения числа решаемых уравнений рационализируют составление и решение уравнений Кирхгофа, применяя для расчета метод контурных токов, узловых потенциалов. Метод основан на применении второго закона Кирхгофа и позволяет сократить при расчете сложных систем число решаемых уравнений. Во взаимно независимых контурах, где для каждого контура хотя бы одна ветвь входит только в этот контур, рассматривают условные контурные токи во всех ветвях контура. Контурные токи в отличие от токов ветвей имеют свои индексы и их направление в контуре целесообразно выбирать одинаковым, например, по часовой стрелке. Уравнения составляют по второму закону Кирхгофа для контурных токов. Токи ветвей выражают через контурные токи по первому закону Кирхгофа. Число выбираемых контуров и число решаемых уравнений равно числу уравнений, составляемых по второму закону Кирхгофа: k = b – y + 1. Сумма сопротивлений всех резистивных элементов каждого контура со знаком плюс является коэффициентом при токе контура. Знак коэффициента при токе смежных контуров зависит от совпадения или несовпадения направления смежных контурных токов. ЭДС входит в уравнение со знаком плюс, если направление ЭДС и направление тока контура совпадают.

Число независимых уравнений, описывающих процессы в сложной электрической цепи, можно существенно сократить, воспользовавшись методом контурных токов, предложенных Д. К. Максвеллом.

Суть метода состоит в том, что вместо фактических токов ветвей находят фиктивные контурные токи, циркулирующие в независимых контурах. При этом ток в любой ветви равен алгебраической сумме контурных токов, проходящих по этой ветви.

Пример. Рассчитать методом контурных токов токи в цепи, схема которой приведена на рисунке 1.

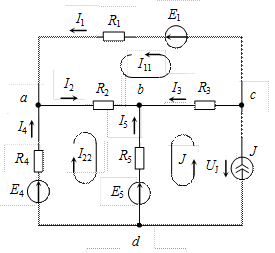
Рис.1

Дано: E₁ = 50 B, E₄ = 150 B, E₅ = 30 B, J = 3 А, R₁ = 10 Ом, R₂ = 15 Ом, R₃ = 5 Ом, R₄ = 5 Ом, R₅ = 25 Ом.

Решение. Выберем положительные направления токов ветвей и укажем их на схеме стрелками. Схема содержит три независимых контура, в одном из которых контурный ток выберем равным току источника тока J. Два других контурных тока обозначим I₁₁ и I₂₂ соответственно и укажем их направление. Составим систему линейных алгебраических уравнений

R₁₁I₁₁ + R₁₂I₂₂ + R₁₃ J = E_11;

R₂₁I₁₁ + R₂₂I₂₂ + R₂₃ J = E_22,

где R₁₁ = R₁ + R₂ + R₃ = 30 Ом; R₂₂ = R₂ + R₄ + R₅ = 45 Ом; R₁₂ = R₂₁ = R₂ = 15 Ом;

R₁₃ = – R₃ = 5 Ом; R₂₃ = R₅ = 25 Ом; E₁₁ = E₁ = 50В; E₂₂ = E₄ – E₅ = 120 В.

Подставим числовые значения и получим систему уравнений

30I₁₁ + 15I₂₂ = 65;

15I₁₁ + 45I₂₂ = 45,

решив которую найдем контурные токи I₁₁ = 2 А, I₂₂ = 0,333 А.

Токи в ветвях равны алгебраической сумме контурных токов, проходящих по этим ветвям:

I₁ = I₁₁ = 2 А; I₂ = I₁₁ + I₂₂ = 2,333 А; I₃ = – I₁₁ + J = 1 A; I₄ = I₂₂ = 0,333 А;

I₅ = – I₂₂ – J = – 3,333 A.

Ток I₅ имеет направление, противоположное выбранному.

ПОРЯДОК ВЫПОЛНЕНИЯ

1. Произвольно выбрать положительные направления токов в ветвях исходной схемы.

2. Произвольно выбрать положительные направления контурных токов для каждого независимого контура электрической схемы. Если в схеме есть ветви с источниками тока, то сначала выбирают контурные токи таким образом, чтобы каждый из них проходил по ветви с источником тока и совпадал с ним по направлению. Таким образом, эти контурные токи J_i будут заранее известны. Остальные контурные токи выбирают проходящими по ветвям, не содержащим источников тока.

3. Обходя каждый из независимых контуров в выбранном направлении, записать n линейных алгебраических уравнений следующего вида:

R₁₁I₁₁ + R₁₂I₂₂ + … + R_1kI_kk + … + R_1nI_nn + 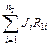= E_11;

… …

R_k1I₁₁ + R_k2I₂₂ + … + R_kkI_kk + … + R_knI_nn + 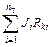= E_kk; (1.1)

… …

R_n1I₁₁ + R_n2I₂₂ + … + R_nkI_kk + … + R_nnI_nn + 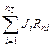= E_nn,

где R_kk – собственное сопротивление контура k, равное сумме сопротивлений всех ветвей контура k; значения R_kk всегда записывают со знаком “плюс”; R_kn – общее сопротивление контуров k и n, причем, R_kn = R_nk; общее сопротивление контуров записывается со знаком “плюс”, если контурный ток I_kk совпадает по направлению с контурным током I_nn, в противном случае оно записывается со знаком “минус”; _ki – общее сопротивление контура k и контура i, по которому циркулирует ток источника тока J_i; знак R_ki выбирают по тем же правилам, что и сопротивления R_kn; E_kk – контурная ЭДС, равная алгебраической сумме ЭДС контура k; ЭДС, действующие в направлении обхода контура, берут со знаком „плюс“, а направленные встречно – со знаком “минус”.

4. Вычислить истинные токи в ветвях в виде алгебраических сумм контурных токов, протекающих по соответствующим ветвям.

Контрольные вопросы:

1. Какое число контуров данной схемы учитывается в методе контурных токов?

2. В чем заключается метод контурных токов?

3. Типовая программа контроля знаний.

3.1. Какое количество независимых уравнений, необходимо для расчета тока в ветвях электрической цепи, изображенной на рис.2.

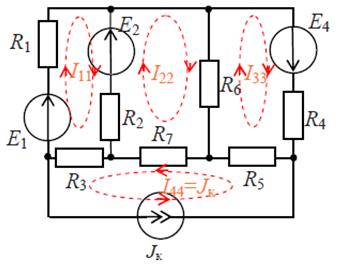Рис.2

3.2. Составьте по методу контурных токов уравнения для цепи, изображенной на рис.2

ЛАБОРАТОРНАЯ РАБОТА №3