Численные методы решения задачи Коши.

При использовании численных методов выполняется замена отрезка [х₀, X] - области непрерывного изменения аргумента х множеством 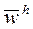. состоящего из конечного числа точек х₀ < х₁ < ... < x_n = Х - сеткой.

При этом x_i называют узлами сетки.

Во многих методах используются равномерные сетки с шагом:

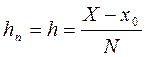
Задача Коши, определённая ранее на непрерывном отрезке [х₀, X], заменяется её дискретным аналогом - системой уравнений, решая которую можно последовательно найти значения y₁, y₂,…,y_n - приближённые значения функции в узлах сетки.

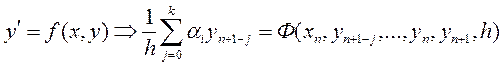
Численное решение задачи Коши широко применяется в различных областях науки и техники, и число разработанных для него методов достаточно велико. Эти методы могут быть разделены на следующие группы.

• Одношаговые методы, в которых для нахождения следующей точки на
кривой у = f(x) требуется информация лишь об одном предыдущем шаге.
Одношаговыми являются метод Эйлера и методы Рунге - Кутта.

• Методы прогноза и коррекции (многошаговые), в которых для отыскания следующей точки кривой у = f(x) требуется информация более чем об одной из предыдущих точек. Чтобы получить достаточно точное численное значение, часто прибегают к итерации. К числу таких методов относятся методы Милна, Адамса - Башфорта и Хемминга.

• Явные методы, в которых функция Ф не зависит от y_n+1.

• Неявные методы, в которых функция Ф зависит от y_n+1.

Метод Эйлера.

Иногда этот метод называют методом Рунге-Кутта первого порядка точности.

Данный метод одношаговый. Табулирование функции происходит поочередно в каждой точке. Для расчета значения функции в очередном узле необходимо использовать значение функции в одном предыдущем узле.

Пусть дано дифференциальное уравнение первого порядка:

Y’ = f(x, y)

с начальным условием

y(x₀) = y₀

Выберем шаг h и введём обозначения:

x_i = х₀ + ih и y_i = y(x_i), где i = 0, 1, 2, ...,

x_i - узлы сетки,

y_i - значение интегральной функции в узлах.

Иллюстрации к решению приведены на рисунке 2.

Проведем прямую АВ через точку (x_i, y_i) под углом α. При этом tg α = f(x_i, y_i)

В соответствий с геометрическим смыслом задачи, прямая АВ является касательной к интегральной функции. Произведем замену точки интегральной функции точкой, лежащей на касательной АВ.

Тогда y_i+1 = y_i + Δy

Из прямоугольного треугольника ABC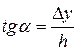

Приравняем правые части tg α = f(x_i, y_i) и 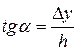. Получим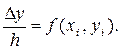

Отсюда Δу = h ∙ f(x_i, y_i).

Подставим в это выражение формулу y_i+1 = y_i + Δy, а затем преобразуем его. В результате получаем формулу расчета очередной точки интегральной функции:

.

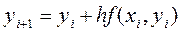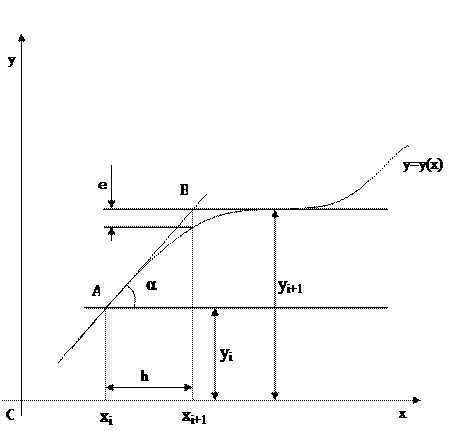Рисунок 2. Метод Эйлера.

Из формулы 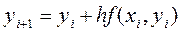видно, что для расчета каждой следующей точки интегральной функции необходимо знать значение только одной предыдущей точки. Таким образом, зная начальные условия, можно построить интегральную кривую на заданном промежутке.

Блок-схема процедуры решения дифференциального уравнения методом Эйлера приведена на рисунке 3.

F(x, у) - заданная функция – должна

h = (Xk – X0)/N

быть описана отдельно.

Входные параметры:

i = 0, …, N - 1

Х0, XK—начальное и конечное

значения независимой переменной;

x = X0 + i ∙ h

Y0 – значение y₀ из начального условия

y(x₀) = y₀;

Yi+1 = Yi + h ∙ F(x, Yi)

N - количество отрезков разбиения;

Выходные параметры:

У - массив значений искомого решения

End

в узлах сетки.

Рисунок 3. Блок-схема процедуры решения дифференциального уравнения методом Эйлера.

Метод Эйлера - один из простейших методов численного решения обыкновенных дифференциальных уравнений. Но существенным его недостатком является большая погрешность вычислений. На рисунке 2 погрешность вычислений для i-гo шага обозначена ε. С каждым шагом погрешность вычислений увеличивается.