Первісна та її властивості, невизначений інтеграл. Основні методи інтегрування
Ф-ція F(x) назив. первісною для ф-ції у=f(x), якщо 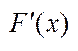 =f(x).
=f(x).
Властивості: Якщо 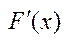 =f(x),
=f(x), 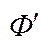 (х)= f(x), то
(х)= f(x), то
F(x)-Ф(х)=с=const.
Дов.: 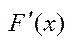 -
- 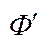 (х)=
(х)= 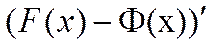 =
= 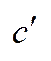 =0.
=0.
Множина або сукупність всіх первісних для даної ф-ції f(x) назив. невизначеним інтегралом: 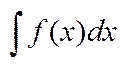 =F(x)+с.
=F(x)+с.
Властив.:1)Диференціал від інтеграла = підінтегральному виразу: 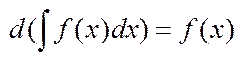 ; 2)Інтеграл суми =сумі інтегралів; 3)Сталий множник можна винести за знак інтеграла.
; 2)Інтеграл суми =сумі інтегралів; 3)Сталий множник можна винести за знак інтеграла.
Методи інтегрування:
1)Безпосереднього інтегрування(табличне);
2) Підстановки.
П-д: 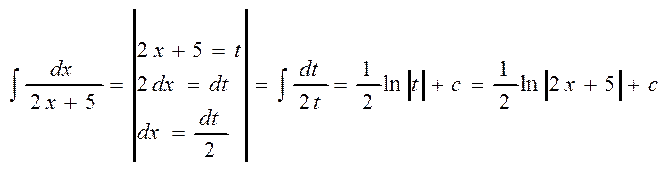 ;
;
3) Інтегрування частинами: 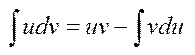 . Методом інтегрування частинами зручно обчислювати такі інтеграли а)
. Методом інтегрування частинами зручно обчислювати такі інтеграли а) 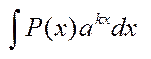 ,
, 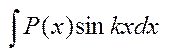 , де Р(х)-многочлен, який слід взяти за u, а за dv – вираз, що залишився. б)
, де Р(х)-многочлен, який слід взяти за u, а за dv – вираз, що залишився. б) 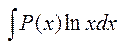 ,
, 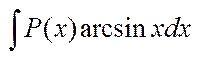 ,де Р(х)dx слід взяти за dv.
,де Р(х)dx слід взяти за dv.
Інтегрув. раціональних ф-й зводиться до інтегрування елементарних дробів: 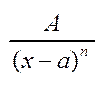 і
і 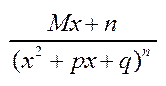 (n є N).
(n є N). 
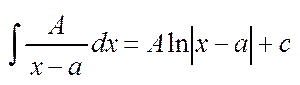 ;
; 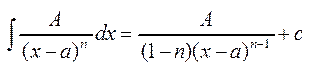 ;
;
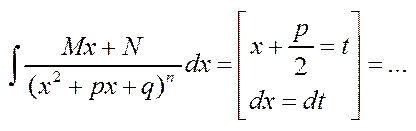
Інтегрування біномних диференціалів:
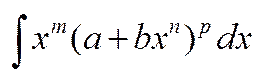 , де m,n,p
, де m,n,p 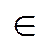 Q,ab
Q,ab 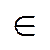 R.
R.
1)p 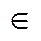 Z,
Z, 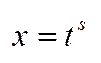 , де S=НСК знаменників n,m, dx=
, де S=НСК знаменників n,m, dx= 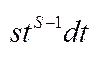 .
.
2)p 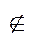 Z,p=
Z,p= 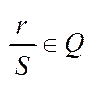 :
:
a) 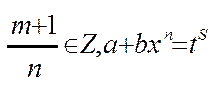 ,s-знаменник р.
,s-знаменник р.
б) 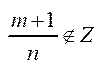 , тоді шук.
, тоді шук. 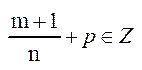 , тоді буде така підстановка
, тоді буде така підстановка 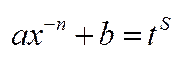 .
.
Інтегрування тригонометричних ф-й:
1) 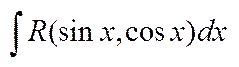 . Універс. підстановка
. Універс. підстановка
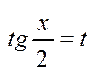 ,
, 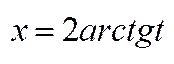 ,
, 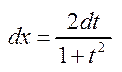 .
.
2) 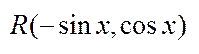 ,
, 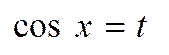 ,
,
-sinxdx=dt, 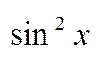 =
= 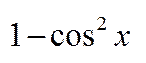 =
= 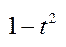 .
.
3) R(sinx , -cosx), sinx=t, cosxdx=dt.
4) R(-sinx , -cosx)= R(sinx ,cosx).
Визначений інтеграл та умови його існування. Формула Ньютона-Лейбніца, вивчення інтеграла в школі.
Задача про обчислення площі кривої трапеції.
Обчислити площу криволінійної трапеції, обмеженої зверху зверху кривою у=f(х), f(х) є С [а, в], f(х)>=0; знизу віссю 0х, у=0; зліва х = а; зправа х = в.
Для розв’язання цієї задачі поступаємо так:
1.
@ ділимо основу трапеції, тобто [а, в] точками хі довільним способом на n чистин. (будемо мати n-1 точок) х1<x2<x3<…<xі-1<хі<…<хn-1.
@ довжину кожного відрізка хі - xі-1 = 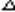 хі.
хі.
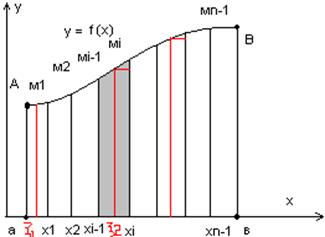
@ одержали відрізки [а, х1], [х1, х2], …, [xі-1, хі]…[ хn-1, в] – частинні відрізки;
@ через кожну із точок хі провод. прямі перпенд. до 0х до перетину з кривою у=f(х).
2.
@ На кожному із частинних відрізків ∆хі вибир. дов. т. 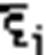 .
.
@ В цих точках постав. перпенд.
@ Через кожну з точок 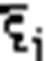 провед. пряму.
провед. пряму.
@ одержимо n прямокутників.
@ довжина основи кожного з них є ∆хі , а висотами значення функції в цій точці.
3.
@ Площа одного такого прям. дорівнює: Si = f(  )*∆хі (i=1, …n).
)*∆хі (i=1, …n).
@ Суму цих площ позначимо: 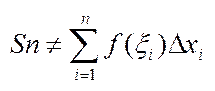 .
.
@ Очевидно, що це не буде площа цієї трапеції, а буде наближено до неї. 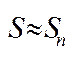
4.
@ Тому природно, за площу криволінійної трапеції аАВв прийм. границю даної суми, якщо вона існує. 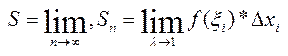 .
.
@ 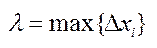 .
.
Задача з механіки.
Обчислити роботу, яку викон. змінна сила F при переміщ. матеріальної точки з полож. А у полож. В, яка діє у напрямку переміщення. 
Для розв’язання цієї задачі поступ. так:
1.
@ ділимо шлях [а, в] точками Si (i=1, … , n-1) довільно на n частин;
@ Тоді Si - Si -1 = ∆Sі ;
2.
@ Вибир. 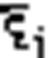 є [Si -1, Si].
є [Si -1, Si].
@ Будемо вважати, що на кожному із відрізків ∆Sі це сила стала і дорівнює з-ню її в т. 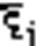 . F (
. F (  ).
).
3. Аі = F ( 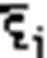 )∆Sі
)∆Sі
Аn = 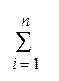 F (
F ( 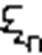 )∆Sі
)∆Sі
А 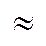 Аn
Аn
Природно, що за роботу, яку викон. це сила F на в-ку [а, в] слід прийняти:
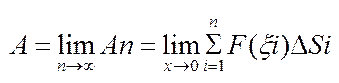 ;
; 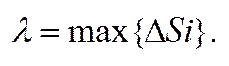
Обидві зад. привели нас до обчисл. однотипних границь.
2. Нехай задана функція у=f(х), х є [а, в].
1. Ділимо в-зок [а, в] дов. способом на т. хі на n частин.
Довжину кожного із в-ків хі – хі-1 = ∆хі.
Ці в-ки назив. частинними.
2. На кожному з цих частин. в-ків вибир. довільно 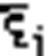 і обчисл. з-ня в кожній з цих точок.
і обчисл. з-ня в кожній з цих точок.
3. Склад. суму добутків:
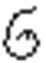 =
= 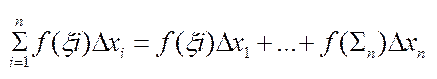 .
.
Це сума назив. інтегр. сумою на в-ку [а, в].
4. В-ня: Границя інтегральної суми 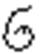 при умові, що
при умові, що 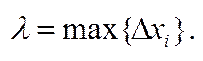 , якщо вона існує і не залежить ні від способу розвит. в-ка [а, в] на част. в-ки, ні від вибору точок
, якщо вона існує і не залежить ні від способу розвит. в-ка [а, в] на част. в-ки, ні від вибору точок 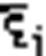 на кожному з них назив. визначеним інтегралом від ф-ції f(х) на в-ку [а, в] і познач.:
на кожному з них назив. визначеним інтегралом від ф-ції f(х) на в-ку [а, в] і познач.: 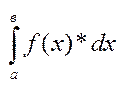 , де а, в – межі інтегрування; а – нижня; в – верхня; f(х) – підінтегр функції; f(х)dx – підінтегр. вираз.
, де а, в – межі інтегрування; а – нижня; в – верхня; f(х) – підінтегр функції; f(х)dx – підінтегр. вираз.
Отже, за визнач. маємо 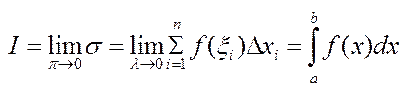 .
.
Познач: 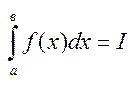 , тоді
, тоді 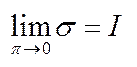 .
.
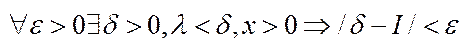 .
.
Геометричний зміст.Див. зад. 1 (площина кр. трап.).
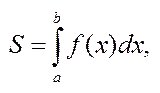 де
де 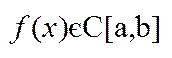 ,
, 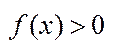 .
.
Механічний зміст. 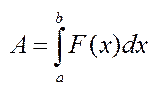 .
.
Див. зад. 2.
Суми Дарбу. Надалі будемо вважати не обхід. умова викон. 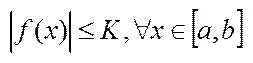
Очевидно, що якщо f (x) неперервна, то за І т. Веєри вона обмежена і на цьому в-ку прим. своє найб. і найм. значення. 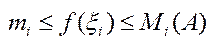 , тобто [хі-1, хі].
, тобто [хі-1, хі]. 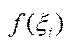 лежить між ті і Мі.
лежить між ті і Мі. 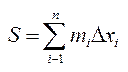 ,
, 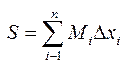 . Назив нижньою (S) і верхньою (S) інтегральними сумами для фун-ції f (x) , або сумами Дербу. Якщо А помнож. на хі і просумув., то матимемо
. Назив нижньою (S) і верхньою (S) інтегральними сумами для фун-ції f (x) , або сумами Дербу. Якщо А помнож. на хі і просумув., то матимемо 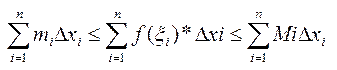 , то очевидно, що
, то очевидно, що 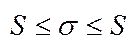 . Будь-яка інтегр. сума лежить між інтегр. сумами Дарбу. Тоді S, S – точні межі для інт. суми б.
. Будь-яка інтегр. сума лежить між інтегр. сумами Дарбу. Тоді S, S – точні межі для інт. суми б.
Умови існування інтеграла. Для того, щоб інтеграл існував необхідно і достатньо, щоб 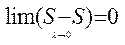 .
. 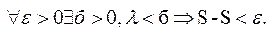
Доведення:
1. Необхідність.
Припустимо, що 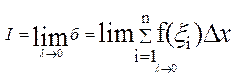 інтеграл існує, тобто
інтеграл існує, тобто 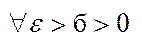 ,
, 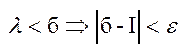 .
. 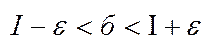 , але суми S і S при заданому розбитті є для інтегральних сум б відповідно точними верхньою і нижньою границями. Тому для них матиме місце нерівність. Із
, але суми S і S при заданому розбитті є для інтегральних сум б відповідно точними верхньою і нижньою границями. Тому для них матиме місце нерівність. Із 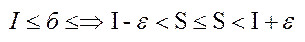 ,
, 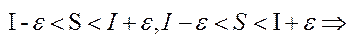
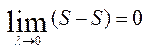 .
.
2. Доступність:
Дано: Нехай 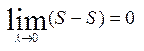 , тоді з цієї умови і умови
, тоді з цієї умови і умови 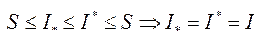 , тоді
, тоді 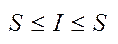 , але тоді
, але тоді 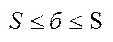 ,
, 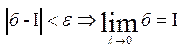 .
.
Умови існування визн. інтегр. можна сформулюв. і через колив. фун-ції, яке має практичне застосування.
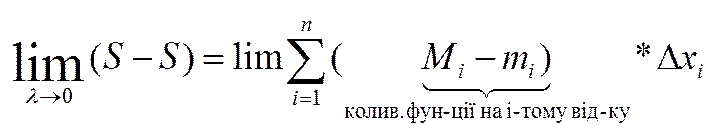 .
.
Тоді, 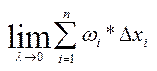 .
.
