Вопрос 6.2. Необходимые и достаточные условия интегрируемости
Теорема 6.2. (Необходимое условие интегрируемости функции). Если функция 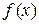 интегрируема на некотором отрезке
интегрируема на некотором отрезке 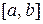 , то она ограничена на этом отрезке.
, то она ограничена на этом отрезке.
Доказательство. Предположим противное, что функция 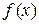 неограниченна, но интегрируема на отрезке
неограниченна, но интегрируема на отрезке 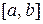 . Пусть T разбиение отрезка интегрирования. Тогда на одном из отрезков разбиения
. Пусть T разбиение отрезка интегрирования. Тогда на одном из отрезков разбиения 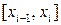 функция неограниченна и за счет выбора промежуточной точки
функция неограниченна и за счет выбора промежуточной точки 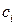 из этого отрезка разбиения слагаемое
из этого отрезка разбиения слагаемое 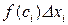 , а, следовательно, и вся интегральная сумма, может быть сделано сколь угодно большим по модулю. Поэтому интегральные суммы такой функции не имеют предела, что противоречит исходному утверждению.
, а, следовательно, и вся интегральная сумма, может быть сделано сколь угодно большим по модулю. Поэтому интегральные суммы такой функции не имеют предела, что противоречит исходному утверждению.
Конец доказательства.
Из теоремы 6.2. следует, неограниченные на отрезках функции не интегрируемы. Но условие ограниченности функции не является достаточным. Приведем пример ограниченной, но не интегрируемой функции.
Пример 6.1. (Функция Дирихле). На отрезке 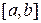 определена функция
определена функция 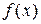 так, что
так, что 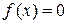 , если х иррационально, и
, если х иррационально, и 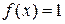 , если х рационально. Покажем, что эта функция не интегрируема по Риману, хотя она, очевидно, ограничена. Действительно, возьмем произвольное разбиение отрезка
, если х рационально. Покажем, что эта функция не интегрируема по Риману, хотя она, очевидно, ограничена. Действительно, возьмем произвольное разбиение отрезка 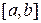 и составим интегральную сумму
и составим интегральную сумму 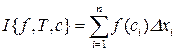 . Если на отрезках разбиения
. Если на отрезках разбиения 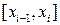 выбрать рациональные значения
выбрать рациональные значения 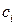 , то интегральные суммы для произвольного разбиения равны 0. Если на отрезках разбиения
, то интегральные суммы для произвольного разбиения равны 0. Если на отрезках разбиения 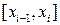 выбрать иррациональные значения
выбрать иррациональные значения 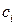 , то интегральные суммы для произвольного разбиения равны
, то интегральные суммы для произвольного разбиения равны 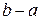 . Следовательно, такие интегральные суммы не имеют предела.
. Следовательно, такие интегральные суммы не имеют предела.
Конец доказательства.
Теорема 6.3. Если определенная и ограниченная на отрезке 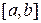 функция
функция 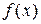 имеет счетное (конечное или бесконечное) число точек разрыва, то она интегрируема на этом отрезке.
имеет счетное (конечное или бесконечное) число точек разрыва, то она интегрируема на этом отрезке.
Эта теорема приводится без доказательства. Отметим, что функция Дирихле ограничена, но имеет разрыв 1-го рода в каждой точке отрезка 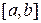 . Так как множество чисел отрезка
. Так как множество чисел отрезка 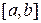 несчетно, то функция Дирихле не удовлетворяет условиям теоремы 6.3. Из теоремы 6.3. следует ряд важных следствий.
несчетно, то функция Дирихле не удовлетворяет условиям теоремы 6.3. Из теоремы 6.3. следует ряд важных следствий.
Следствие 6.1. Непрерывная на отрезке 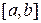 функция
функция 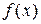 интегрируема на этом отрезке.
интегрируема на этом отрезке.
Следствие 6.2. Кусочно-непрерывная на отрезке 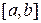 функция
функция 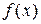 интегрируема на этом отрезке.
интегрируема на этом отрезке.
Приведем еще один класс интегрируемых функций.
Теорема 6.4. Монотонная на отрезке 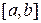 функция
функция 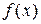 интегрируема на этом отрезке.
интегрируема на этом отрезке.
Эта теорема приводится без доказательства.
Замечание 6.1. Монотонная на отрезке 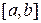 функция
функция 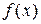 ограничена на этом отрезке значениями
ограничена на этом отрезке значениями 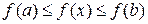 . Следовательно, монотонные функции на отрезках удовлетворяют необходимым условиям интегрируемости (теорема 6.2).
. Следовательно, монотонные функции на отрезках удовлетворяют необходимым условиям интегрируемости (теорема 6.2).
Конец замечания.
Замечание 6.2. Отметим без доказательства, что монотонная на отрезке 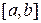 функция
функция 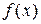 может иметь только счетное (конечное или бесконечное) число точек разрыва первого рода. По этой причине монотонные функции на отрезках удовлетворяют достаточным условиям интегрируемости (теорема 6.3).
может иметь только счетное (конечное или бесконечное) число точек разрыва первого рода. По этой причине монотонные функции на отрезках удовлетворяют достаточным условиям интегрируемости (теорема 6.3).
Конец замечания.
Рассмотрим теперь геометрический смысл определенного интеграла. Пусть T произвольное разбиение отрезка 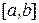 и
и 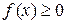 . На каждом отрезке разбиения построим прямоугольник, высота которого равна наименьшему значению функции на этом отрезке. Очевидно, что полученная фигура будет вписана в соответствующую криволинейную трапецию. Обозначим площадь вписанной ступенчатой фигуры
. На каждом отрезке разбиения построим прямоугольник, высота которого равна наименьшему значению функции на этом отрезке. Очевидно, что полученная фигура будет вписана в соответствующую криволинейную трапецию. Обозначим площадь вписанной ступенчатой фигуры 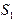 . Аналогично можно построить описанную ступенчатую фигуру, выбирая на каждом отрезке разбиения высоту, равную максимальному значению функции на отрезке разбиения. Ее площадь обозначим через
. Аналогично можно построить описанную ступенчатую фигуру, выбирая на каждом отрезке разбиения высоту, равную максимальному значению функции на отрезке разбиения. Ее площадь обозначим через 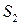 . В зависимости от разбиения T значения
. В зависимости от разбиения T значения 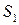 и
и 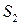 будут меняться. Если максимальное значение
будут меняться. Если максимальное значение 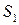 равно минимальному значению
равно минимальному значению 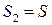 , то S называют площадью плоской фигуры. Можно показать, что если
, то S называют площадью плоской фигуры. Можно показать, что если 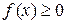 и интегрируема, то криволинейная трапеция, соответствующая функции
и интегрируема, то криволинейная трапеция, соответствующая функции 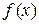 имеет площадь
имеет площадь 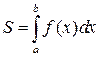 .
.
