Диодная теория выпрямления запорного слоя Шоттки
Сопротивление слоя Шоттки существенно зависит от полярности подаваемого на него напряжения. При подаче положительного потенциала на полупроводник относительно металлического электрода ширина слоя, обедненная носителями заряда (d), а следовательно, и сопротивление слоя возрастают. Наоборот, при подаче напряжения противоположной полярности ширина ОПЗ может быть уменьшена почти до нуля. При этом сопротивление контакта металл - полупроводник существенно понижается. Таким образом, запорный слой Шоттки должен обладать свойством выпрямления переменного тока.
Длина свободного пробега электронов (l) в полупроводнике значительно больше ширины ОПЗ и, следовательно, рассеянием носителей при пролете через эту область можно пренебречь.
Так как l пропорциональна подвижности электронов µn, а ширина ОПЗ 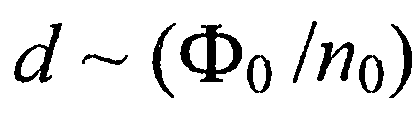 , то при фиксированном значении Ф0 критерий применимости диодной теории
, то при фиксированном значении Ф0 критерий применимости диодной теории  должен выполняться прежде всего для полупроводников с высокой подвижностью и большой концентрацией основных носителей заряда. Будем считать, что падением напряжения на сопротивлении объема полупроводника можно пренебречь и что зазор между металлом и полупроводником является для электронов туннельно прозрачным. В термодинамически равновесных условиях термоэлектронные потоки из металла в полупроводник и в обратном направлении одинаковы. Причем эти потоки создаются электронами, энергия которых превышает высоту потенциального барьера над уровнем Ферми: Фб = Ф0 - F
должен выполняться прежде всего для полупроводников с высокой подвижностью и большой концентрацией основных носителей заряда. Будем считать, что падением напряжения на сопротивлении объема полупроводника можно пренебречь и что зазор между металлом и полупроводником является для электронов туннельно прозрачным. В термодинамически равновесных условиях термоэлектронные потоки из металла в полупроводник и в обратном направлении одинаковы. Причем эти потоки создаются электронами, энергия которых превышает высоту потенциального барьера над уровнем Ферми: Фб = Ф0 - F
Из выражения (8) следует, что плотность потока таких электронов
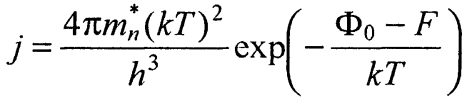 (27)
(27)
При подаче внешнего напряжения такой полярности, при которой отрицательный потенциал приходится на полупроводник, высота потенциального барьера для электронов, пересекающих контакт справа налево, уменьшится на еU(рис.3,а), а плотность их потока соответственно увеличится. Поток электронов из металла в полупроводник останется без изменения, т.к. на высоту потенциального барьера, преодолеваемого этими электронами, внешнее напряжение не влияет.
Для плотности тока через слой Шоттки можно записать следующее выражение:
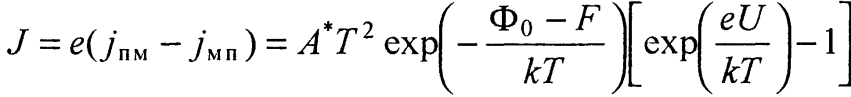 (28)
(28)
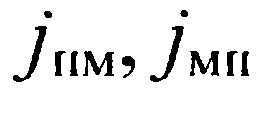 - плотности потока электронов из полупроводника в металл и наоборот;
- плотности потока электронов из полупроводника в металл и наоборот; 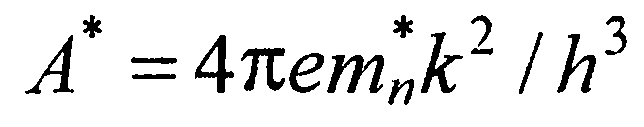 . Для электронов с
. Для электронов с 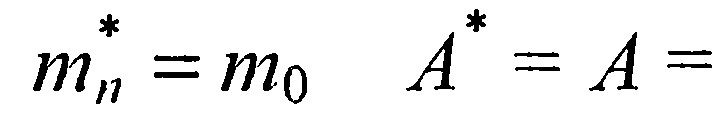
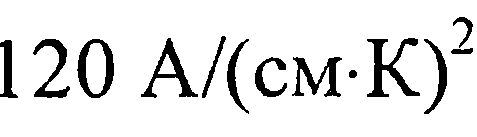 называется постоянной Ричардсона для термоэлектронной эмиссии в вакуум. Для полупроводников n-типа с изотропной эффективной массой электронов в самых низких минимумах энергии зоны проводимости
называется постоянной Ричардсона для термоэлектронной эмиссии в вакуум. Для полупроводников n-типа с изотропной эффективной массой электронов в самых низких минимумах энергии зоны проводимости 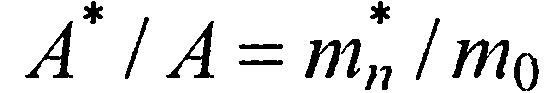
В случае многодолинного полупроводника (типа Ge и Si) постоянная Ричардсона для одного минимума имеет вид
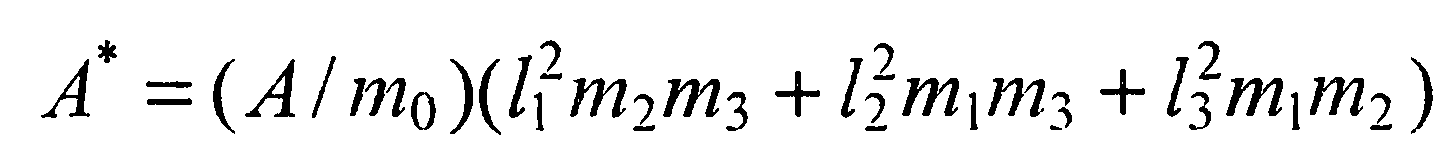 (29)
(29)
где 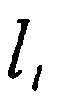 - косинусы углов между нормалью к плоскости контакта и главными осями эллипсоида, представляющего собой изоэнергетическую поверхность для электронов в k-пространстве, а m1, m2 и m3 - компоненты тензора обратной эффективной массы. Выражении (28)
- косинусы углов между нормалью к плоскости контакта и главными осями эллипсоида, представляющего собой изоэнергетическую поверхность для электронов в k-пространстве, а m1, m2 и m3 - компоненты тензора обратной эффективной массы. Выражении (28) 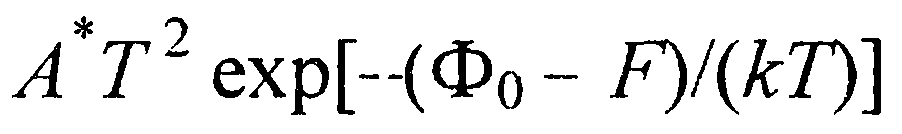 не зависит от подаваемого напряжения и называется плотностью тока насыщения.
не зависит от подаваемого напряжения и называется плотностью тока насыщения.
Обозначая его через Js, перепишем соотношение (28) в следующем виде:
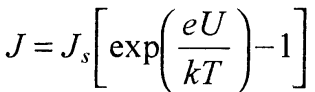 (30)
(30)
При U« кТ/е экспоненту в этом выражении можно разложить в ряд, ограничиваясь вторым членом. Тогда
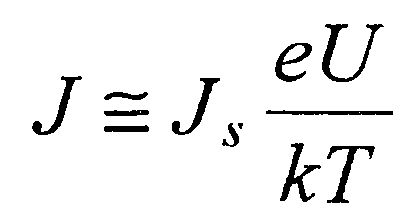 (31)
(31)
т.е. вольтамперная характеристика слоя Шоттки в области малых напряжений описывается законом Ома. Если 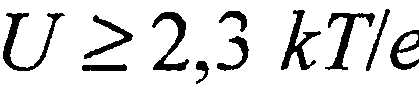 , то
, то 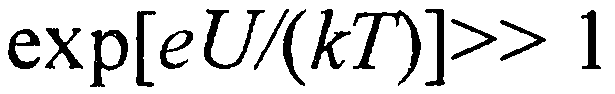 и
и 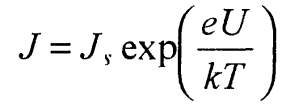 (32)
(32)
Таким образом, при больших напряжениях плотность тока через слой Шоттки растет с увеличением U по экспоненциальному закону. Ток, соответствующий рассмотренному знаку разности потенциалов, называется прямым током. При подаче на запорный слой разности потенциалов противоположного знака (на полупроводнике положительный потенциал) высота потенциального барьера для электронов, переходящих из полупроводника в металл, возрастает на eU (рис. 3,б), а их поток уменьшится по сравнению с потоком в равновесных условиях, когда U=0. Теперь преобладающим будет поток электронов из металла в полупроводник, величина которого не зависит от U и определяется формулой (27). Если U достаточно велико, то потоком электронов из полупроводника можно пренебречь и тогда плотность тока через контакт
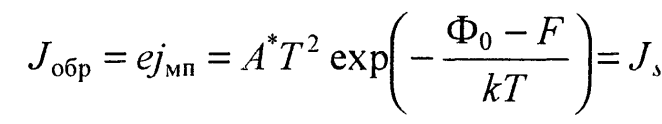 (33)
(33)
Этот ток называется обратным. Такой же результат можно получить из выражения (30), меняя знак U на противоположный. Действительно, в этом случае
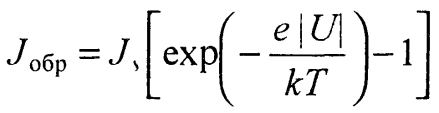 (34)
(34)
При | U |«кТ/е вольтамперная характеристика будет опять описываться законом Ома, а при
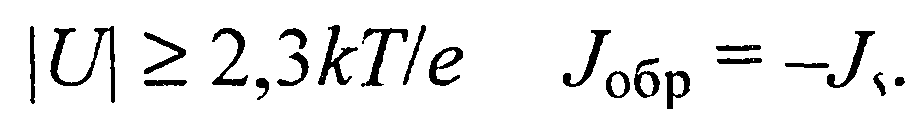 Знак минус говорит о том, что обратный ток течет в отрицательном направлении оси Ох. Общий вид вольт-амперной характеристики контакта с запорным слоем представлен на рис. 4 кривой 1.
Знак минус говорит о том, что обратный ток течет в отрицательном направлении оси Ох. Общий вид вольт-амперной характеристики контакта с запорным слоем представлен на рис. 4 кривой 1.
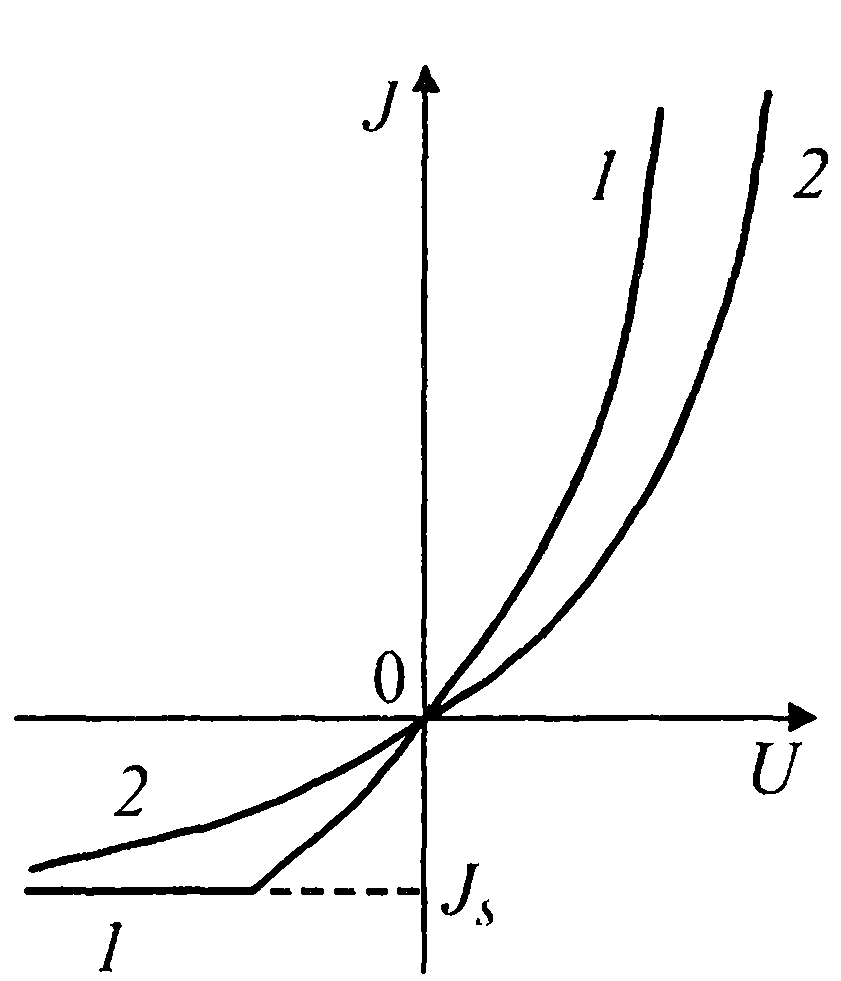
Рис. 4 Вольтамперные характеристики запорного слоя Шоттки согласно диодной G) и диффузионной B) теориям выпрямления
