Понятие статики в теории автоматического управления

Как и всякая динамическая система, САУ может находиться в одном из двух режимов - стационарном (установившемся) и переходном. В свою очередь стационарный режим так же подразделяется на два вида - статический и динамический.

Статический режим (статика) - это режимы, при котором система находится в состоянии покоя вследствие того, что все внешние воздействия и параметры самой системы не меняются во времени.

Динамический стационарный режим возникает, когда приложенные к системе внешние воздействия изменяются по какому-либо установившемуся закону, в результате чего система приходит в режим установившегося вынужденного движения.

Стационарные динамические режимы в свою очередь бывают двух типов. Детерминированный динамический стационарный режим - это режим, при котором на систему действует детерминированное (регулярное) стационарное воздействие. Примером такого режима является установившейся гармонический режим, описываемый рассмотренными выше частотными характеристиками.

Случайный стационарный режим является установившемся в статическом смысле и имеет место, когда приложенные к системе воздействия представляют собой случайные, но стационарные функции времени.

Нашей задачей является рассмотрение статики САУ, т.е. режим установившегося состояния. При этом изучают соотношение отдельных величин, характеризующих состояние системы.

Уравнения статики можно получить тремя путями:

1) решая совместно систему статических (алгебраических) уравнений звеньев;

2) используя преобразования структурных схем в статическом режиме;

3) из уравнений динамики.

Так как статический режим есть установившийся, то в случае устойчивой системы отсутствует приращение функции при любом приращении аргумента (времени), т.е. Dy=0 при любом Dt¹0. Это означает, что все производные в дифференциальных уравнениях, описывающих поведение координат системы управления, равны нулю. Например, уравнения апериодического звена:

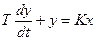, (5.1)

и колебательного:

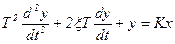, (5.2)

примут вид:

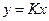, (5.3)

т.е. уравнения звеньев, входящих в любую статическую систему значительно упрощаются, принимают одинаковый вид.

Тогда последовательное соединение звеньев можно представить одним эквивалентным звеном с коэффициентом передачи

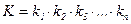, (5.4)

где k₁, k₂,..., k_n - коэффициенты передачи последовательно соединенных звеньев.

При параллельном соединении звеньев коэффициент передачи эквивалентного звена равен сумме коэффициентов передачи параллельно соединенных звеньев.

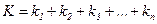, (5.5)

При встречно-параллельном соединении звеньев коэффициент передачи эквивалентного звена равен дроби, числитель которой представляет собой передаточный коэффициент основного звена, а знаменатель - единицу минус или плюс произведение передаточных функций основного звена и звена обратной связи.

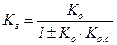, (5.6)

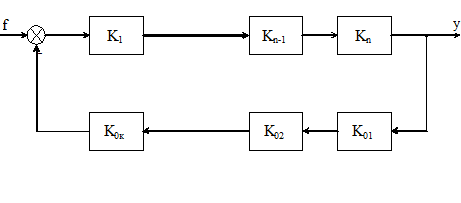
Рисунок 5.1 Структурная схема замкнутой САУ в

статическом режиме

Нетрудно показать, что коэффициент передачи замкнутой САУ по данному возмущению f равен отношению коэффициента передачи прямого канала от точки приложения возмущения до выходной величины к передаточному коэффициенту разомкнутой САУ, увеличенному на единицу (рисунок 5.1)

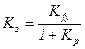, (5.7)

где

;

;

.

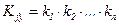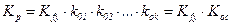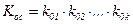Преобразования структурных схем для статического режима ничем не отличаются от преобразования структурных схем, содержащих динамические звенья. Становится так же очевидным, что уравнения статики САУ получаются из уравнений динамики:

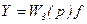, (5.8)

если подставить в него p=0, что соответствует постоянству всех переменных, т.е. равенству нулю всех производных.

В результате имеем следующее уравнение статики:

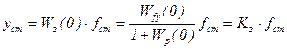, (5.9)

Здесь y_ст - статическое упрощение выходной величины САУ, вызванное приращением внешнего воздействия f_ст.

Итак, статический режим САУ - установившийся режим, для которого приращение выходной величины равно нулю при неизменных управляющих и возмущающих воздействиях, т.е. статический режим устанавливается в устойчивых САУ по окончании переходного процесса. Этому отвечает равенство p=0 в уравнениях динамики, что соответствует постоянству всех переменных и равенству нулю всех производных.

Уравнение статики (5.9) - уравнение в отклонениях, в которых статическое приращение выходной величины может вызываться как управляющим, так и возмущающим воздействиями.

Выражение (5.7) определяет статическое отклонение выходной величины САУ, вызванное установившимся приращением внешнего воздействия f (рисунок 5.2, а). В этом случае мы имеем дело с относительными значениями величины, т.е. уравнения (5.7, 5.9) записаны в отклонениях. Если перейти к абсолютным значениям величины, то статическая характеристика системы примет вид, представленный на рисунке 5.2, б.

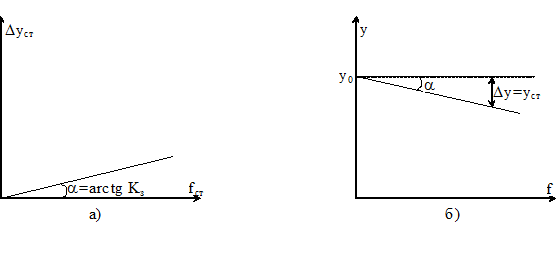
Рисунок 5.2 Статические характеристики САУ

Из выражений (5.7 и 5.8) можно определить величину статического отклонения y, приходящуюся на единицу воздействия f:

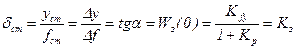, (5.10)

Эта величина является мерой статической точности системы и называется статизмом.

В качестве примера рассмотрим статический режим уже знакомой нам системы автоматического регулирования напряжения генератора (рисунок 1.4). Пользуясь математическим описанием элементов САР (2.35, 2.43) и считая, что регулятор напряжения реализует пропорциональный закон управления (1.11), а так же учитывая (1.4¸1.20), получим структурную схему, представленную на рисунке 5.3.

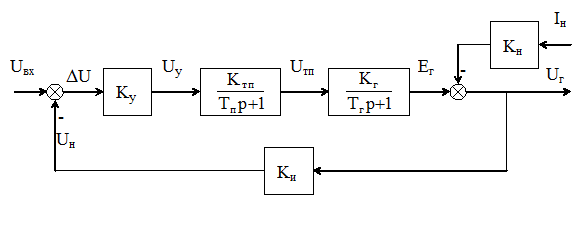
Рисунок 5.3 Структурная схема статической системы автоматического регулирования напряжения генератора

Передаточная функция этой системы по возмущению в виде изменения тока нагрузки I_н имеет вид:

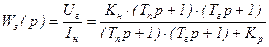, (5.11)

где .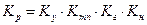

Отсюда статизм системы регулирования напряжения генератора:

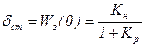, (5.12)

Если предположить, что регулирование отсутствует, т.е. контур разомкнут, то получим естественную зависимость напряжения от нагрузки:

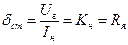, (5.13)

которая определяется значением K_н=R_я. Пусть K_н=R_я=0,2. В этом случае при изменении тока нагрузки на 100% (обычно за 100% принимают номинальное значение) напряжение генератора изменится на 20%.

Если коэффициент передачи разомкнутой системы K_p=100, то при замыкании системы статизм составит

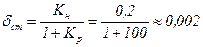, (5.14)

Очевидно, что замыкание системы привело к уменьшению статизма системы.

Таким образом, применение автоматического регулирования и отрицательной обратной связи привело к повышению статической точности поддержания напряжения в (1+K_p) раз. Увеличения статической точности можно добиться, увеличивая K_y. Однако, добиться таким образом полного устранения статизма системы невозможно, т.к. K_y имеет конечные значения и ограничено многими факторами.