Вероятностная модель системы массового обслуживания

Для изучения закономерностей в поведении СМО применяют аналитические методы. Их суть состоит в получении моделей в виде математических соотношений, уравнений для интересующих характеристик СМО. Решая эти уравнения, можно получить зависимости нужных характеристик от всех параметров модели.

Вернемся к основным понятиям, определяющим СМО. Это, во-первых, поток входящих вызовов, во-вторых, один или несколько обслуживающих приборов, и, наконец, очередь, в которой может находиться случайное число ожидающих обслуживания вызовов (заявок, требований, сообщений). СМО функционирует во времени, т.е. преобразует входной поток вызовов в поток обслуженных вызовов.

Поскольку принципиальным аспектом работы СМО является случайный характер входного потока вызовов, то все математические модели СМО будут вероятностными, которые описываются стохастическими уравнениями. Их решения будут определять некоторые распределения вероятностей для дискретных случайных величин или плотности вероятности для непрерывных случайных величин. Во многих случаях знание распределений не является необходимым, и тогда исследуемые характеристики будут описываться некоторыми средними - математическим ожиданием, дисперсией и т.п.

Практически все известные аналитические результаты удается получить, опираясь на математический аппарат, разработанный российским математиком А.А. Марковым.

Случайный процесс называется марковским, если будущее поведение процесса не зависит ни от каких сведений о прошлом. Наиболее важным для дальнейшего использования является класс непрерывных цепей (случайных процессов) Маркова называемых «процессами гибели - размножения». Для таких случайных процессов будущие состояния СМО зависят от прошлого только через текущее состояние СМО.

Пусть 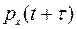- вероятность нахождения пучка линий в состоянии 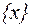(вероятность занятия x каналов)в момент времени 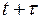, где x = 0, ..., V , а 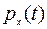- та же вероятность в момент времени t.

Согласно определению марковского процесса за промежуток времени 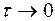может произойти не более одного элементарного события. Поэтому, если в момент времени 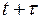пучок перейдет в состояние 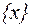, то это возможно при наступлении за время 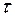одного из трех событий:

- в момент времени 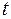пучок находился в состоянии 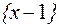,и за время 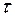поступил один вызов;

- в момент времени 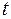пучок находился в состоянии 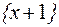, а за время 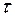произошло одно освобождение;

- в момент времени 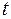пучок находился в состоянии 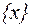, а за время 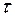не поступил вызов, и не произошло освобождение.

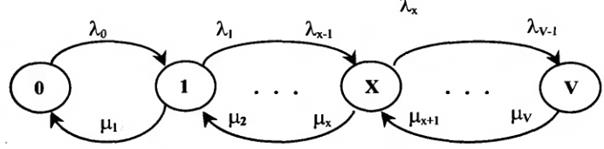
Графически вероятностные процессы часто изображают в виде диаграммы переходов, в которой соседние состояния соединяются линиями, отображающими интенсивности переходов между ними (рисунок 3.7).

Состояние 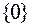– все каналы свободны;

состояние 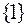– один канал занят;

состояние 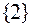– два канала занято;

…………..

состояние 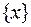– 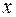каналов занято;

состояние 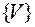– 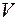каналов занято.

Рисунок 3.7 – Диаграмма переходов СМО

Вероятность поступления в состоянии 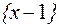за время 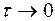хотя бы одного вызова

.

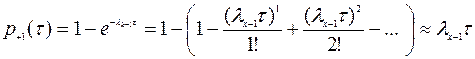Вероятность освобождения в состоянии 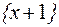за время 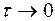хотя бы одного канала пучка

.

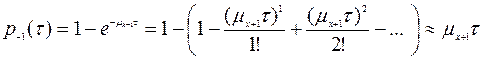Вероятность нахождения пучка за время 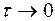в том же состоянии

.

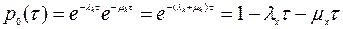Запишем вероятность 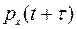как

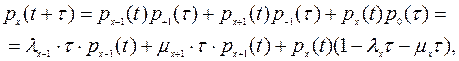
где x = 0, ..., V.

Перейдя к пределу при 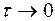, получим

;

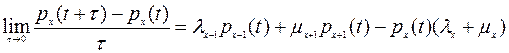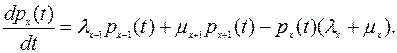
Учитывая, что 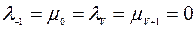, получаем систему дифференциальных уравнений

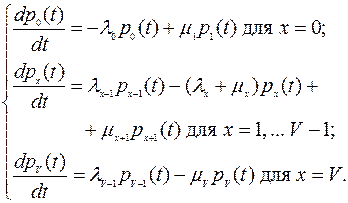
Далее, будем считать, что исследование проводится для установившегося (стационарного) режима, в котором вероятности состояний не зависят от времени наблюдения, т.е.,

.

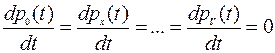Поэтому можно считать, что 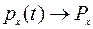, где 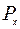- стационарная вероятность занятия точно 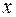каналов пучка. Следовательно

для :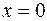

;

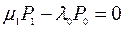для :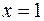

;

.

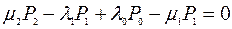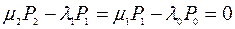Таким образом, можно получить, что

,

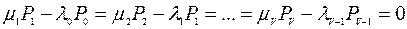или, иначе

;

;

…

;

…

.

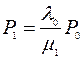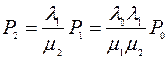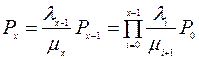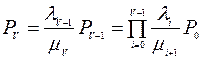Из условия нормировки 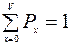находим, что

,

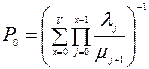а затем

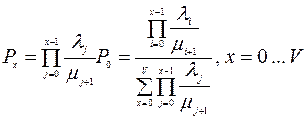. (3.6)