Преобразований Лоренца
Согласно принципу относительности все физические законы должны быть сформулированы так, чтобы они оставались инвариантными относительно преобразований Лоренца – как говорят, релятивистски или Лоренц-инвариантными.
Законы механики не являются Лоренц-инвариантными, поэтому они должны быть видоизменены. Требование инвариантности физических законов относительно некоторых преобразований не является специфической особенностью СТО. Ясно например, что вследствие изотропии пространства, содержание физического закона, скажем, второго закона Ньютона
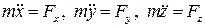 (1)
(1)
не может зависеть от ориентации координатных осей. При любом повороте осей в пространстве уравнения (1) остаются неизменными, т.к. каждая из проекций силы и ускорения преобразуется по одному и тому же закону.
Это свойство можно сформулировать так: в классической физике все законы формулируются в виде равенств типа
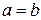 , (2)
, (2)
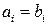 , (3)
, (3)
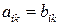 , (4)
, (4)
связывающих величины одинаковой тензорной размерности. Например, (3) связывает векторы. При повороте, в частности, вокруг вокруг оси z на угол 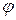 компоненты радиус-вектора преобразуются по закону
компоненты радиус-вектора преобразуются по закону
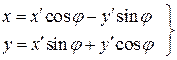 (5)
(5)
Поскольку по этому закону преобразуются компоненты любых векторов, а не только компоненты радиус-вектора, то (3) не нарушается.
Итак, любой физический закон должен быть сформулирован так, чтобы он содержал только величины одинаковой тензорной размерности. В классической механике законы преобразования координат, которые должны оставлять неизменными физические законы, сводятся к следующим:
1) Инвариантность относительно преобразований Галилея
2) Инвариантность относительно пространственных переносов и поворотов систем координат (однородность и изотропия простанства)
3) Инвариантность относительно замены 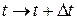 (однородность времени)
(однородность времени)
4) Инвариантность относительно замены 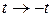 (обратимость времени, указывающая на симметрию законов механики относительно прошлого и будущего).
(обратимость времени, указывающая на симметрию законов механики относительно прошлого и будущего).
СТО вместо требования (1) выдвигает более общее требование инвариантности физических законов относительно преобразований Лоренца. Условия (2) - (4) сохраняются и в СТО.
Один из способов, позволяющий установить Лоренц-инвариантную форму физических законов, состоит вследующем.
Введем формально величину
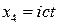 , (6)
, (6)
которую будем называть четвертой координатой или мнимым временем. Это мнимая величина не имеющая прямого физического смысла. Если обозначить, как обычно 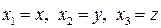 , то с помощью (6) интервал можно представить в виде
, то с помощью (6) интервал можно представить в виде
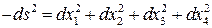 . (7)
. (7)
Будем считать 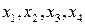 ортогональными координатами в некотором абстрактном четырехмерном пространстве. Преобразование Лоренца – это линейное преобразование этих координат, оставляющее неизменной величину
ортогональными координатами в некотором абстрактном четырехмерном пространстве. Преобразование Лоренца – это линейное преобразование этих координат, оставляющее неизменной величину 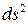 .Но с геометрической точки зрения -
.Но с геометрической точки зрения - 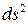 суть квадрат расстояния между двумя точками в четырехмерном пространстве. То есть преобразование Лоренца - это такое линейное преобразование, которое не изменяет расстояние между двумя точками.в четырехмерном пространстве. Из геометрии известно, что имеется только два только два таких преобразования –параллельный перенос и вращение. Первое –это тривиальное преобразование, сводящееся к изменению начала отсчета системы координат x,y,z,ict. Поэтому единственным нетривиальным линейным преобразованием, оставляющим неизменным интервал – является поворот в четырехмерном пространстве x,y,z,ict.
суть квадрат расстояния между двумя точками в четырехмерном пространстве. То есть преобразование Лоренца - это такое линейное преобразование, которое не изменяет расстояние между двумя точками.в четырехмерном пространстве. Из геометрии известно, что имеется только два только два таких преобразования –параллельный перенос и вращение. Первое –это тривиальное преобразование, сводящееся к изменению начала отсчета системы координат x,y,z,ict. Поэтому единственным нетривиальным линейным преобразованием, оставляющим неизменным интервал – является поворот в четырехмерном пространстве x,y,z,ict.
Такая геометрическая интерпретация преобразований Лоренца принадлежит Минковскому и позволяет непосредственно сделать вывод о релятивистски инвариантной форме физических законов. Соответствующие выражения должны иметь вид
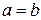 , (8)
, (8)
где 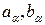 -скаляры, или
-скаляры, или
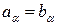 , (9)
, (9)
где 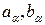 - 4-х мерные векторы,
- 4-х мерные векторы, 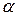 =1,2,3,4, и в общем случае
=1,2,3,4, и в общем случае
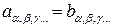 , (10)
, (10)
где 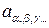 - четырехмерные тензоры произвольного ранга.
- четырехмерные тензоры произвольного ранга.
При поворотах координатных осей в четырехмерном пространстве Минковского (x,y,z,ict) все величины, входящие в релятивистски-инвариантные выражения, преобразуются по одному закону, поэтому равенства (8)-(10) не нарушаются.
Эти условия инвариантности в четырехмерном пространстве являются непосредственным аналогом условий инвариантности при повороте системы координат в реальном трехмерном пространстве.
Представление о четырехмерном пространстве имеет формальный характер, а четвертая координата ict, будучи мнимой, не имеет непосредственного физического смысла. Тем не менее, введение этой координаты вполне оправданно, указывая, в частности, на неразрывную связь пространства и времени. Заметим, что четвертую координату не обязательно вводить как величину мнимую.
Убедимся, что преобразование поворота в пространстве(x,y,z,ict) идентично преобразованию Лоренца. Для простоты считаем, что движение происходит в направлении совмещенных осей 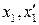 . Это отвечает повороту в плоскости
. Это отвечает повороту в плоскости 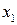 и
и 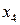 при неизменной ориентации осей
при неизменной ориентации осей 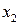 и
и 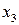 . Если обозначить через
. Если обозначить через 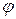 угол поворота, то
угол поворота, то
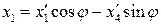 , (11)
, (11)
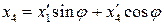 . (12)
. (12)
Для 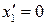 будем иметь
будем иметь
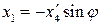 ,
,
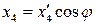 .
.
Отсюда
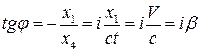 , (13)
, (13)
где V – скорость равномерного движения начала координат системы  относительно системы
относительно системы  .
.
Из (13) следует, что
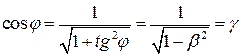 ,
,
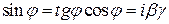 ,
,
откуда
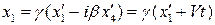 ,
,
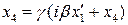 , или
, или 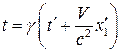 .
.
Эти формулы совпадают с фомулами обратного преобразования Лоренца.
