Пример выполнения задания. Даны механическая система в начальном положении (рисунок 11а) и следующие исходные данные: m1/m = 1; m2/m = 0,5; m3/m = 0,2; m4/m = 1,4; R2 = 25 см; R3 = 20

Даны механическая система в начальном положении (рисунок 11а) и следующие исходные данные: m₁/m = 1; m₂/m = 0,5; m₃/m = 0,2; m₄/m = 1,4; R₂ = 25 см; R₃ = 20 см; r₂ = 0,5R₂; r₃ = 0,5R₃; i_2x = 20 см; i_3x = 20 см; f = 0,15; a = 30°; s = 2 м.

Найти скорость груза 1 u₁ в конечном положении.

Решение. Применим теорему об изменении кинетической энергии механической системы. Для рассматриваемой системы, состоящей из абсолютно твердых тел, соединенных абсолютно гибкими, нерастяжимыми нитями (идеальными внутренними связями):

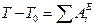, (27)

где T и Т₀ – кинетическая энергия системы в конечном и начальном положении соответственно;

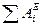– сумма работ внешних сил, приложенных к системе, на перемещении системы из начального положения в конечное.

Так как в начальном положении система находится в покое, то Т₀ = 0. Тогда уравнение (27) принимает вид:

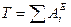. (28)

Для определения кинетической энергии Т и суммы работ внешних сил изобразим механическую систему в конечном положении, когда тело 1 пройдет путь s (рисунок 11б).

Составим кинематические соотношения между скоростями и перемещениями точек системы, при этом скорости и перемещения выразим соответственно через скорость и перемещение груза 1.

Скорость нити, соединяющей тела 1 и 2, равна искомой скорости груза 1 u₁. Она же является вращательной скоростью для точек обода барабана 2:

,

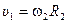откуда угловая скорость барабана 2

.

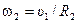Скорость нити, соединяющей тела 2 и 3, равна

.

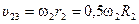Тогда

,

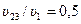откуда

.

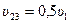С другой стороны, для блока 3 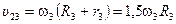, откуда угловая скорость блока 3

.

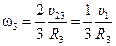Скорость груза 4, центра масс блока 3 и нити, соединяющей их, равна

.

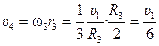Теперь рассмотрим перемещения тел 3 и 4 в зависимости от перемещения тела 1 на величину s. Барабан 2 испытывает только вращательное движение. Для барабана 2 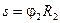, откуда угол его поворота .

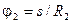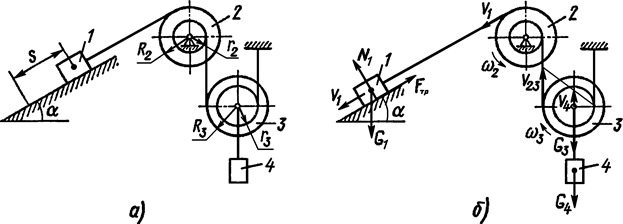
Рисунок 11 – Схема механизма (а) и расчетная схема (б)

Перемещение нити, соединяющей тела 2 и 3: .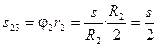

Угол поворота блока 3 относительно неподвижной нити равен:

.

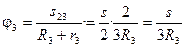Тогда величина подъема груза 4 и центра масс блока 3 составит:

.

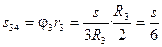Итак, при перемещении груза 1 на величину s барабан 2 повернется на угол 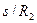, а блок 3 – на угол 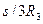. При этом блок 3 и груз 4 поднимутся на величину .

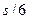Теперь вычислим кинетическую энергию системы в конечном положении Т как сумму кинетических энергий тел 1–4:

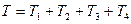. (29)

Кинетическая энергия груза 1, движущегося поступательно, равна:

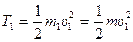. (30)

Для барабана 2, совершающего вращение вокруг неподвижной оси, кинетическая энергия определится, как

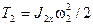, (31)

где 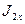– момент инерции барабана относительно оси его вращения:

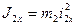. (32)

Теперь формула (31) с учетом уравнения будет выглядеть:

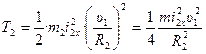. (33)

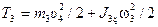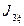Кинетическая энергия блока 3, совершающего плоское движение, , где – момент инерции блока относительно оси, проходящей через его центр масс: .

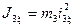Тогда, с учетом полученных выше выражений, получим:

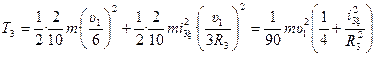. (34)

Для груза 4, движущегося поступательно:

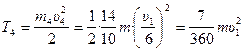. (35)

Итак, кинетическая энергия системы в конечном положении с учетом формул (30), (33)–(35) определится, как

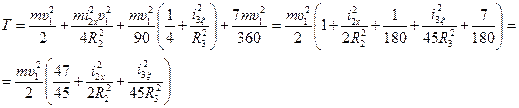
или

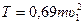. (36)

Теперь вычислим сумму работ всех внешних сил, приложенных к системе, на заданном перемещении. Силы, действующие на систему, показаны на рисунке 11б.

Работа силы тяжести груза 1: 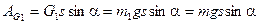. (37)

Работа силы трения скольжения груза 1:

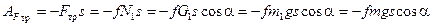. (38)

Работа сил тяжести блока 3 и груза 4 на их общем перемещении :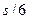

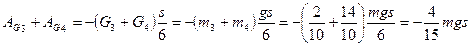. (39)

Тогда сумма работ внешних сил определится с учетом формул (37)–(39), как

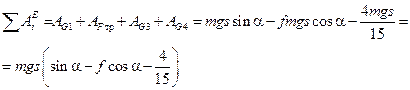
или

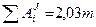. (40)

Теперь формула (28) с учетом уравнений (36) и (40) примет вид:

,

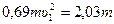откуда искомая скорость груза 1 в конечном положении:

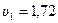м/с.

Аналитическая механика

Задание Д.16. Применение принципа Даламбера к определению динамических реакций связей (опор)

Определить динамические реакции внешних связей (опор) механической системы (таблица 14):

а) в произвольный момент времени – для вариантов 4, 5, 10, 12–18, 21–30;

б) в момент времени t = t₁ – для вариантов 1, 8, 9, 11, 20;

в) в тот момент времени, когда угол поворота φ= φ₁, – для вариантов 2, 3, 6, 7;

г) в положении, показанном на чертеже для вариантов 15 и 19.

На схемах (таблица 14) плоскость хOу (хАу) горизонтальна, плоскость yOz (yAz) вертикальна. Необходимые для решения данные приведены в таблице 15, в которой ω – угловая скорость, φ₀ и ω₀ – значения угла поворота и угловой скорости в начальный момент времени.

Примечания

1. Вращающиеся тела, для которых не указан радиус инерции, рассматривать как тонкие однородные стержни (варианты 1–5, 11–15, 18, 19, 23, 24, 29, 30) или сплошные однородные диски (варианты 6–9, 16, 20, 22, 28); в варианте 10 тело 2 рассматривать как материальную точку.

2. На схемах 1, 8, 9, 11, 16, 17, 20–22 указаны внешние моменты М.