Основной приём решения иррациональных интегралов – это замена переменной, которая избавит нас от ВСЕХ корней в подынтегральной функции
Отмечу, что эта замена немного своеобразная, ее техническая реализация отличается от «классического» способа замены, который рассмотрен на уроке Метод замены в неопределенном интеграле.
В данном примере нужно провести замену 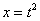 , то есть, вместо «икса» под корнем у нас окажется
, то есть, вместо «икса» под корнем у нас окажется 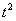 . Почему замена именно такая? Потому-что
. Почему замена именно такая? Потому-что 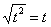 , и в результате замены корень пропадёт.
, и в результате замены корень пропадёт.
Если бы в подынтегральной функции вместо квадратного корня у нас находился 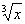 , то мы бы провели замену
, то мы бы провели замену 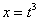 . Если бы там был
. Если бы там был 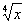 – то
– то 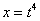 и так далее.
и так далее.
Хорошо, 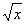 у нас превратится в
у нас превратится в 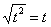 . Что произойдет с многочленом
. Что произойдет с многочленом 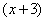 ? Сложностей нет: если
? Сложностей нет: если 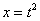 , то
, то 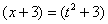 .
.
Осталось выяснить, во что превратится дифференциал 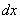 . Делается это так:
. Делается это так:
Берем нашу замену 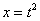 и навешиваем дифференциалы на обе части:
и навешиваем дифференциалы на обе части:
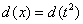
(я распишу максимально подробно)
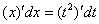
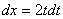
Оформление решения должно выглядеть примерно так:
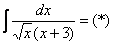
Проведем замену: 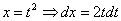

(1) Проводим подстановку после замены (как, что и куда, уже рассмотрено).
(2) Выносим константу за пределы интеграла. Числитель и знаменатель сокращаем на  .
.
(3) Получившийся интеграл является табличным, готовим его для интегрирования, выделяя квадрат
(4) Интегрируем по таблице, используя формулу 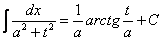 .
.
(5) Проводим обратную замену. Как это делается? Вспоминаем, от чего плясали: если 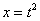 , то
, то 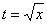 .
.
Внимание! Для изучения дальнейших примеров необходимо хорошо проработать первый параграф урока Интегрирование некоторых дробей.
Пример 2
Найти неопределенный интеграл
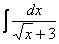
Это пример для самостоятельного решения. Полное решение и ответ в конце урока.
Как-то так получилось, что в примерах 1, 2 «голый» числитель с одиноким дифференциалом 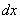 . Что же. Исправим ситуацию.
. Что же. Исправим ситуацию.
Пример 3
Найти неопределенный интеграл
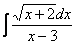
Предварительный анализ подынтегральной функции опять показывает, что лёгкого пути нет. А поэтому нужно избавляться от корня.
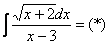
Проведем замену: 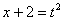
За 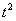 обозначаем ВСЁ выражение под корнем. Замена из предыдущих примеров
обозначаем ВСЁ выражение под корнем. Замена из предыдущих примеров 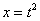 здесь не годится (точнее, сделать-то её можно, но это не избавит нас от корня).
здесь не годится (точнее, сделать-то её можно, но это не избавит нас от корня).
Навешиваем дифференциалы на обе части:
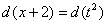
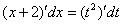
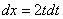
С числителем разобрались. Что делать с 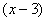 в знаменателе?
в знаменателе?
Берем нашу замену 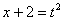 и выражаем из неё:
и выражаем из неё: 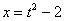
Если 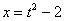 , то
, то 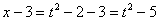
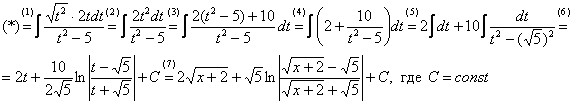
(1) Проводим подстановку в соответствии с выполненной заменой.
(2) Причесываем числитель. Константу здесь я предпочел не выносить за знак интеграла (можно делать и так, ошибкой не будет)
(3) Раскладываем числитель в сумму. Еще раз настоятельно рекомендую ознакомиться с первым параграфом урока Интегрирование некоторых дробей. Канители с разложением числителя в сумму в иррациональных интегралах будет предостаточно, очень важно отработать это прием.
(4) Почленно делим числитель на знаменатель.
(5) Используем свойства линейности неопределенного интеграла. Во втором интеграле выделяем квадрат 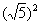 для последующего интегрирования по таблице.
для последующего интегрирования по таблице.
(6) Интегрируем по таблице. Первый интеграл совсем простой, во втором используем табличную формулу высокого логарифма 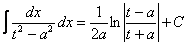
(7) Проводим обратную замену. Если мы проводили замену 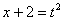 , то, обратно:
, то, обратно: 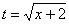
Пример 4
Найти неопределенный интеграл
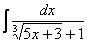
Это пример для самостоятельного решения, если вы невнимательно проработали предыдущие примеры, то допустите ошибку! Полное решение и ответ в конце урока.
Принципиально так же решаются интегралы с несколькими одинаковыми корнями, например 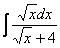 ,
, 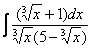 и т.д. А что делать, если в подынтегральной функции корни разные?
и т.д. А что делать, если в подынтегральной функции корни разные?
Пример 5
Найти неопределенный интеграл
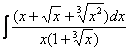
Вот и пришла расплата за голые числители. Когда встречается такой интеграл, обычно становится страшно. Но страхи напрасны, после проведения подходящей замены подынтегральная функция упрощается. Задача состоит в следующем: провести удачную замену, чтобы сразу избавиться от ВСЕХ корней.
Когда даны разные корни удобно придерживаться следующей схемы решения. Сначала выписываем на черновике подынтегральную функцию, при этом все корни представляем в виде 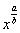 :
: 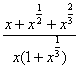 . Нас будут интересовать знаменатели степеней:
. Нас будут интересовать знаменатели степеней:
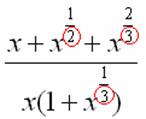
Записываем эти знаменатели: 2, 3, 3.
Теперь нужно найти наименьшее общее кратное чисел 2, 3, 3 – такое число, чтобы оно делилось и на 2 и на 3 (в данном случае), кроме того, это число должно быть как можно меньше.
Очевидно, что наименьшим общим кратным является число 6. Оно делится и на 2 и на 3, кроме того, меньше шестерки ничего не придумать.
Как многие уже догадались, замена в рассматриваемом интеграле будет следующей: 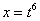
Оформляем решение:
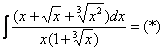
Проведем замену: 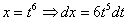
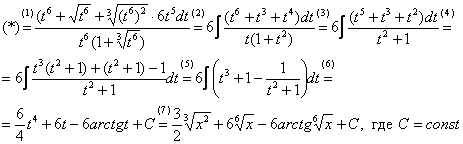
(1) Производим подстановку.
(2) Избавляемся от корней. Выносим константу за знак интеграла. Сокращаем числитель и знаменатель на 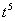 .
.
(3) Сокращаем числитель и знаменатель еще на  .
.
(4) Раскладываем числитель в сумму (как это сделать, уже неоднократно упоминалось).
(5) Почленно делим числитель на знаменатель.
(6) Интегрируем по таблице. При этом константу я снова «прилепил» к каждому из трех слагаемых (можно этого и не делать, момент несущественный).
(7) Проводим обратную замену. Если 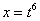 , то, обратно:
, то, обратно: 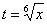 . В ходе обратной замены некоторые корни лучше сразу сократить (обычно это делается устно). В рассмотренном примере сокращение корней встретилось в первом слагаемом:
. В ходе обратной замены некоторые корни лучше сразу сократить (обычно это делается устно). В рассмотренном примере сокращение корней встретилось в первом слагаемом: 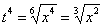
Как видите, особых сложностей нет, несмотря на то, что сначала интеграл показался трудным и страшным.
Пример 6
Найти неопределенный интеграл
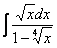
Это пример для самостоятельного решения.
