Иррациональные уравнения, содержащие степени выше второй

Если уравнение имеет вид 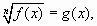то его можно решить , возводя обе части этого уравнения в степень 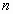. Полученное уравнение 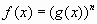при нечетном 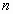равносильно данному уравнению, а при четном 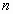является нго следствием, аналогично рассмотренному выше случаю при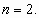

Пример 1

Возведем обе части уравнения в куб:

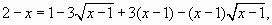или

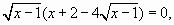которое равносильно совокупности двух уравнений:

Ответ: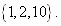

При решении иррациональных уравнений очень часто пользуются следующим приемом.

Если 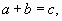то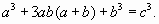

В последнем равенстве заменяют на 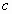и получают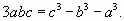

Далее легко избавиться от кубической иррациональности , возводя обе части в куб.

Пример 2.

Здесь, очевидно,

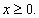
Возведем в куб обе части уравнения, получим:

,

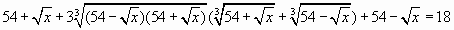или

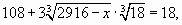
или

или

или

Проверка подтверждает, что это корень уравнения.

Ответ:

Замечание.

Замена в конкретном примере левой части на правую, вообще говоря , неправомерна –ведь нам неизвестно ни одно значение 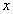, при котором это уравнение превращается в верное числовое равенство. Возможно, таких решений нет вообще. Допуская в практических действиях такую замену, мы фактически расширяем возможное множество решений. Поэтому все найденные решения следует проверять и только те, которые превращают исходное уравнение в верное равенство, следует записать в ответ.

От того, что школьник решит лишний десяток задач, умнее и сообразительнее он не станет, Результат обучения оценивается не количеством сообщаемой информации, а качеством ее усвоения. Это качество будет выше, если на один и тот же пример посмотреть с разных сторон. Решение задач разными способами способствует развитию активного мышления учащихся. Хорошую почву для этого дает решение примеров разными способами.

Пример 3. Способ 1.

(1)

Возведем обе части уравнения в куб:

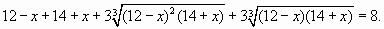
Группируя, получаем:

Используя равенство (1) имеем:

или

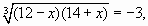
или

или

корни которого

Ответ:

Способ 2.

Иногда полезно ввести не одну вспомогательную переменную, а несколько, сводя исходное уравнение к системе уравнений.

Пусть Тогда

Таким образом справедлива следующая система:

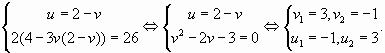
Возвращаясь к переменной 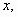находим

Ответ: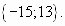

В следующем примере введение вспомогательной переменной сводит исходное уравнение к однородному.

Пример 4.

Положим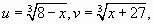

Тогда исходное уравнение примет вид:

Поскольку при котором переменная обращается в нуль, не является решением исходного уравнения ( в чем можно убедиться подстановкой), делим обе части уравнения на

решая которое , находим:

Осталось решить уравнения 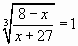и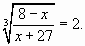

Корнями этих уравнений являются числа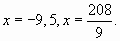

Ответ: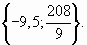

Пример 5.

Область допустимых значений задается неравенством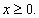

Преобразуем уравнение следующим образом:

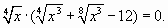
Один корень этого уравнения

Для решения второго уравнения положим

и решим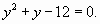

Корни этого уравнения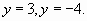

Последний корень не принадлежит указанному промежутку, поэтому, решая уравнение , получим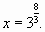

Ответ :