Закон сохранения движения центра масс

Из теоремы о движении центра масс можно получить следующие важные следствия:

1) Пусть сумма внешних сил, действующих на систему, равна нулю

Тогда из уравнения 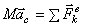следует, что или Следовательно, если сумма всех внешних сил, действующих на систему, равна нулю, то центр масс этой системы движется с постоянной по модулю и направлению скоростью, т. е. равномерно и прямолинейно. В частности, если вначале центр масс был в покое, то он и останется в покое. Действие внутренних сил, как мы видим, движение центра масс системы изменить не может.

2) Пусть сумма внешних сил, действующих на систему, не равна нулю, но эти силы таковы, что сумма их проекций на какую-нибудь ось (например, ось Ох) равна нулю:

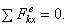
Тогда уравнение 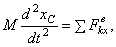дает: или

Следовательно, если сумма проекций всех действующих внеш­них сил на какую-нибудь ось равна нулю, то проекция скорости центра масс системы на эту ось есть величина постоянная. В частности, если в начальный момент , то и в любой после­дующий момент , т.е. центр масс системы в этом случае вдоль оси Ох перемещаться не будет ( ).

Пример 10. Человек перешел с кормы лодки на нос. Определим перемещение лодки s (рис.39). Вес лодки – Р₁, человека – Р₂, длина лодки – l. Сопротивление движению не учитываем.

Определим движение центра масс С системы, состоящей из человека и лодки.

Рис.39

Составляем дифференциальное уравнение движения центра масс по оси х: Но так как проекции внешних сил , и 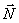на ось х равны нулю, то Проинтегрировав дважды это уравнение, получим и Но в начале движения система была неподвижна Значит,

Найдем координату в первом положении системы, когда человек находился на корме, как координату центра тяжести:

И во втором положении, когда человек перейдет на нос лодки:

Приравниваем координаты, т.к.

Из этого равенства находим перемещение лодки

Теоремы об изменении количества движения точки и механической системы

Количество движения точки

Основными динамическими характеристиками движения точки являются количество движения и кинетическая энергия.

Количеством движения точки называется векторная величина m 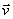равная произведению массы точки на вектор ее скорости. Направлен вектор т 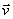так же, как и скорость точки, т. е. по каса­тельной к ее траектории.

Необходимость введения двух динамических характеристик объяс­няется тем, что одной характеристикой нельзя охватить все особен­ности движения точки.

Например, зная количество движения автомобиля (т.е. величину ) а не величины и в отдельности) и действующую на него при торможении силу, можно определить, через сколько секунд автомобиль остановится, но по этим данным нельзя найти пройденный за время торможения путь. Наоборот, зная начальную кинетическую энергию автомобиля и тормозящую силу, можно определить тормоз­ной путь, но по этим данным нельзя найти время торможения.

Импульс силы

Для характеристики действия, оказываемого на тело силой за некоторый промежуток времени, вводится понятие об импульсе силы. Введем сначала понятие об элементарном импульсе, т. е. об импульсе за бесконечно малый промежуток времени dt. Элементарным импульсом силы называйся векторная величина , равная произведению вектора силы 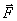на элементарный промежуток времени

.

Направлен элементарный импульс по линии действия силы.

Импульс 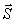любой силы 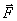за конечный промежуток времени t₁ вычисляется как интегральная сумма соответствующих элементарных импульсов:

.

Следовательно, импульс силы за любой промежуток времени, равен определенному интегралу от элементарного импульса, взятому в пределах от 0 до .

В частном случае, если сила 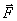и по модулю, и по направлению постоянна ( 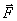=const), будем иметь . Причем, в этом случае и модуль . В общем случае модуль импульса может быть вычислен через его проекции.

Проекции импульса силы на прямоугольные декартовы оси координат равны:

.

Единицей измерения импульса в СИ является –